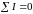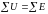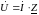- •Методические указания
- •Теоретические основы электротехники
- •Часть 2 – Методы расчета цепей переменного тока Севастополь
- •Лабораторная работа № 1 Тема: «Применение метода комплексных амплитуд для расчета цепей при гармоническом воздействии»
- •Найдём погрешность по напряжениям
- •Токи в ветвях после разветвления:
- •Падение напряжения на катушке
- •Суммарная реактивная мощность всех потребителей
- •Контрольные вопросы
- •Лабораторная работа № 2 Тема: «Исследование резонансных явлений в электрических цепях при гармоническом воздействии»
- •Контрольные вопросы
- •Лабораторная работа № 3 Тема: «Исследование линейной электрической цепи при периодических несинусоидальных токах»
- •3.1 Разложение периодических несинусоидальных кривых в тригонометрический ряд Фурье
- •3.2 Особенности разложения в ряд Фурье кривых, обладающих симметрией
- •3.4 Графоаналитическое разложение кривых в ряд Фурье
М инистерство
образования и науки Украины
инистерство
образования и науки Украины
С евастопольский
национальный технический университет
евастопольский
национальный технический университет
Методические указания
к лабораторному практикуму
по дисциплине
Теоретические основы электротехники
для студентов дневной и заочной форм обучения направления 6.0508 «Микро- и наноэлектроника»
Часть 2 – Методы расчета цепей переменного тока Севастополь
2012
УДК 004.021
Методические указания к выполнению лабораторных работ по дисциплине «Теоретические основы электротехники» для студентов дневной и заочной форм обучения направления 6.0508 «Микро- и наноэлектроника»:/ А.С. Паранюк, Д.Г. Мурзин — Севастополь: Изд-во СевНТУ, 2011.: Методы расчета цепей переменного тока. — 89 с.
Целью методических указаний является оказание помощи студентам в подготовке к выполнению лабораторных работ по дисциплине «Теоретические основы электротехники».
Методические указания предназначены для студентов 3‑го курса, обучающихся по направлению «Микро- и наноэлектроника».
Методические указания рассмотрены и утверждены на заседании кафедры электронной техники (протокол № 5 от 04 ноября 2010 г.).
Рецензент: Астраханцев Александр Владимирович, канд. техн. наук, доцент кафедры электронной техники.
СОДЕРЖАНИЕ
Требования к оформлению отчета к лабораторной работе…….6
Лабораторная работа № 1. Применение метода комплексных амплитуд для расчета цепей при гармоническом воздействии ...XX
Лабораторная работа № 2. Исследование резонансных явлений в электрических цепях при гармоническом воздействии ………....XX
Лабораторная работа № 3. Исследование линейной электрической цепи при периодических несинусоидальных токах ………..…....XX
Библиографический список……………………………………XX
Приложение А. ……………………………XX
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ОТЧЕТА К ЛАБОРАТОРНОЙ РАБОТЕ
Отчет о выполнении лабораторной работы оформляется на стандартных листах формата А4. Расположение листов – вертикальное. Поля: левое 2 см, верхнее 2 см, нижнее 1 см, правое 1 см. Отчет следует оформлять в редакторе Microsoft Word.
Отчет должен включать в себя титульный лист с указанием номера и темы лабораторной работы; цель работы и индивидуальное задание; исследуемую электрическую схему; результаты (экранные формы) моделирования и расчеты; выводы по работе.
Лабораторная работа № 1 Тема: «Применение метода комплексных амплитуд для расчета цепей при гармоническом воздействии»
Цель работы – знакомство с методом комплексных амплитуд для расчета цепей при гармоническом воздействии в пакете MathCad.
Теоретические сведения
1.1. Синусоидальные электрические величины
Электромагнитный процесс в электрической цепи называется периодическим, если значения токов и напряжений повторяются через равные промежутки времени (переменный ток, напряжение).
Токи, мгновенные значения которых повторяются через равные промежутки времени, называются периодическими. На практике широкое применение находит периодический ток, являющийся синусоидальной функцией времени и называемый синусоидальным током.
Мгновенное значение синусоидального тока определяется по формуле:
i(t) = Im sin (ωt + ψi),
где Im – амплитуда тока; (ωt + ψi) – фазовый угол (фаза); ψi – начальная фаза; ω – угловая частота, равная скорости изменения фазы тока.
Периодом – Т синусоидального тока называют наименьший промежуток времени, через который мгновенные значения тока повторяются. Величина, обратная периоду, называется частотой периодического тока
f =1/Т.
Если Т измеряется в секундах, то частота измеряется в герцах (Гц). Связь между ω и f определяется выражением
ω= 2π/Т = 2π f.
При совместном рассмотрении двух синусоидальных величин одной частоты разность их начальных фаз называют сдвигом фаз. Разность фаз напряжения u(t) = Um sin (ωt + ψu) и тока i(t) = Im sin (ωt + ψi) на участке цепи обозначают φ:
φ = ψu – ψi.
Если φ = 0, то говорят, что напряжение и ток совпадают по фазе.
Если φ > 0, то ток i(t) отстает от напряжения u(t) по фазе на угол φ.
Если φ < 0, то ток i(t) опережает напряжение u(t) по фазе на угол φ.
Если φ = ± π, то говорят, что ток i(t) и напряжение u(t) находятся в противофазе.
При
построении временной зависимости
сигналов
если ψi 0
начинают построение с величин t0=
‑ψi,
т.е., при ψi > 0
график смещается влево от начала
координат, а при ψi < 0
– вправо на величину
 (рис. 1.1). Разность начальных фаз двух
синусоидальных функций одной частоты
называется сдвигом их по фазе. Если ψ1
‑ψ2 = 0,
синусоиды совпадают по фазе, а если ψ1
‑ψ2 = ,
они находятся в противофазе.
(рис. 1.1). Разность начальных фаз двух
синусоидальных функций одной частоты
называется сдвигом их по фазе. Если ψ1
‑ψ2 = 0,
синусоиды совпадают по фазе, а если ψ1
‑ψ2 = ,
они находятся в противофазе.
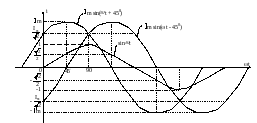 Рисунок
1.1 – Временная зависимость гармонического
сигнала
Рисунок
1.1 – Временная зависимость гармонического
сигнала
Переменный ток характеризуется его действующим значением. Действующее значение переменного тока численно равно такому значению I постоянного тока, который на одном и том же сопротивлении за время одного периода произведет тот же самый тепловой эффект, что и периодический ток. Таким образом, действующее значение периодического переменного тока (действующий ток) равно его среднеквадратичному значению за период:
 .
.
Действующее значение I и амплитуда Im синусоидального тока связаны между собой соотношением:
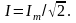
Аналогичные соотношения справедливы для синусоидальных напряжений и ЭДС:
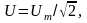
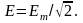
1.2 Изображение синусоидальных функций векторами и комплексными числами
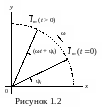
Рассмотрим
гармонический ток, меняющийся по закону
i(t)=Imsin
(ωt+ψi).
Проведем из начала прямоугольной системы
координат под углом ψi
относительно оси абсцисс вектор
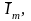 длина
которого в масштабе равна амплитуде
тока Im
(рисунок 1.2).
длина
которого в масштабе равна амплитуде
тока Im
(рисунок 1.2).
Проекция вектора
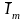 на
ось ординат i(0) = Im
sin ψi,
что соответствует мгновенному значению
тока при t = 0. Если
вектор вращать в положительном направлении
(против движения часовой стрелки) с
угловой частотой ω, то для произвольного
момента времени t его
проекция на вертикальную ось будет
равна мгновенному значению тока i(t)
= Im
sin(ωt
+ ψi).
Таким образом, для сложения двух
синусоидальных токов одинаковой частоты
i1(t)
= I1m
sin (ωt
+ ψ1i)
и i2(t)
= I2msin
(ωt +
ψ2i)
достаточно сложить изображающие их
векторы
на
ось ординат i(0) = Im
sin ψi,
что соответствует мгновенному значению
тока при t = 0. Если
вектор вращать в положительном направлении
(против движения часовой стрелки) с
угловой частотой ω, то для произвольного
момента времени t его
проекция на вертикальную ось будет
равна мгновенному значению тока i(t)
= Im
sin(ωt
+ ψi).
Таким образом, для сложения двух
синусоидальных токов одинаковой частоты
i1(t)
= I1m
sin (ωt
+ ψ1i)
и i2(t)
= I2msin
(ωt +
ψ2i)
достаточно сложить изображающие их
векторы
 и
и
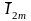 (рисунок
1.3). Проекция полученного при этом вектора
=
+
на вертикальную ось будет равна сумме
мгновенных значений токов i1
и i2: i(t)
= i1(t)
+ i2(t)
= Im
sin (ωt
+ ψi).
Совокупность векторов, изображающих
синусоидально изменяющиеся величины
одинаковой частоты (токи, напряжения,
ЭДС) в заданный момент времени, называют
векторными диаграммами.
(рисунок
1.3). Проекция полученного при этом вектора
=
+
на вертикальную ось будет равна сумме
мгновенных значений токов i1
и i2: i(t)
= i1(t)
+ i2(t)
= Im
sin (ωt
+ ψi).
Совокупность векторов, изображающих
синусоидально изменяющиеся величины
одинаковой частоты (токи, напряжения,
ЭДС) в заданный момент времени, называют
векторными диаграммами.

При построении векторных диаграмм целесообразно располагать векторы для момента времени t = 0, т. к. взаимное расположение векторов остается неизменным для любого момента времени.
Геометрические операции с векторами на практике заменяют операциями с комплексными числами, что существенно упрощает расчеты.
Числа вида
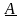 =
a + jb,
где
=
a + jb,
где
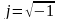 ,
называются комплексными.
,
называются комплексными.
a
= Re[
]
– действительная часть комплексного
числа
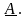
b = Im[ ] – мнимая часть комплексного числа
Приведенная выше
форма записи комплексного числа
называется алгебраической.
Комплексное число
изображается
на комплексной плоскости точкой с
координатами a и
jb или радиусом-вектором,
проведенным из начала координат в эту
точку (рисунок 1.4). Оно может быть также
записано в показательной форме
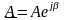 ,
где
,
где
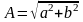 –
модуль комплексного числа, а β =
arc tg b/a
– аргумент комплексного числа.
–
модуль комплексного числа, а β =
arc tg b/a
– аргумент комплексного числа.
Комплексные числа
=
a + jb
и
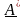 =
a – jb
называются комплексно-сопряженными.
=
a – jb
называются комплексно-сопряженными.
Вектору
в декартовой системе координат
соответствует комплексное число на
комплексной плоскости.
на
комплексной плоскости.
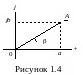
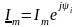 называется
комплексной амплитудой тока.
Вращающемуся с угловой частотой ω
вектору
соответствует
комплексная функция времени, которая
называется комплексным мгновенным
током:
называется
комплексной амплитудой тока.
Вращающемуся с угловой частотой ω
вектору
соответствует
комплексная функция времени, которая
называется комплексным мгновенным
током:
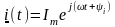 =
Im
cos(ωt
+ ψi)
+ jIm
sin(ωt
+ ψi)
= Re
=
Im
cos(ωt
+ ψi)
+ jIm
sin(ωt
+ ψi)
= Re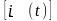 + jIm
.
+ jIm
.
Следовательно, синусоидальный ток i(t) и его изображение комплексной величиной однозначно связаны следующим равенством:
i(t)
=
 =
Im
sin(ωt
+ ψi)
=
Im
sin(ωt
+ ψi)
Функцию
 называют
оператором вращения. Комплексная
величина
называют
оператором вращения. Комплексная
величина
 где
I=
где
I=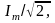 называется
комплексным дейст- вующим током или
просто комплексным током. Таким
образом, для мгновенного значения тока
i(t)
= Im
sin (ωt
+ ψi)
можно записать комплексную амплитуду
и комплексный ток. И наоборот, если
задана комплексная амплитуда тока
(комплексный
ток
называется
комплексным дейст- вующим током или
просто комплексным током. Таким
образом, для мгновенного значения тока
i(t)
= Im
sin (ωt
+ ψi)
можно записать комплексную амплитуду
и комплексный ток. И наоборот, если
задана комплексная амплитуда тока
(комплексный
ток
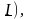 то известны амплитуда (действующее
значение) и начальная фаза тока.
то известны амплитуда (действующее
значение) и начальная фаза тока.
Метод расчета цепей синусоидального тока, основанный на изображении гармонических функций времени комплексными числами, называется методом комплексных амплитуд или комплексным методом расчета.
1.3 Мощность в цепи синусоидального тока
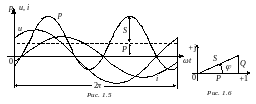
Произведение мгновенного значения приложенного к цепи напряжения u(t) и мгновенного значения проходящего по цепи тока i(t) называют мгновенной мощностью: p(t) = u(t)i(t).
Пусть на входе пассивного двухполюсника
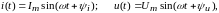
тогда мгновенная мощность [Вт]
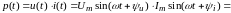
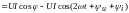
содержит постоянную составляющую и синусоиду двойной частоты (рис. 1.5). Если мгновенные значения тока и напряжения имеют одинаковые знаки, то мгновенная мощность положительна; в противном случае – отрицательна.
Среднее значение мгновенной мощности за период называется активной мощностью:
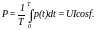
Активная мощность измеряется в ваттах (Вт) и характеризует энергию, которая передается от источника к нагрузке, где она превращается в другие виды энергии.
Множитель cosφ называют коэффициентом мощности. Чем больше cosφ, тем больше активная мощность при заданных действующих значениях напряжения U и тока I.
Произведение действующих значений напряжения U и тока I называют полной мощностью:
S = UI.
Полная мощность измеряется в вольт-амперах (ВА) и характеризует предельную мощность источника при cos(φ) = 1.
При расчетах электрических цепей используется также понятие реактивной мощности:
Q = UIsin(φ).
Реактивная мощность характеризует энергию, которая периодически циркулирует между источником и нагрузкой. Она измеряется в вольт-амперах реактивных (вар). При индуктивной нагрузке (φ > 0) реактивная мощность положительна, а при емкостной нагрузке (φ < 0) отрицательна.
Активная P, реактивная Q и полная S мощности связаны между собой соотношениями прямоугольного треугольника (треугольника мощностей рис.1.6):
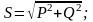 P=
S cosφ; Q
= S sinφ.
P=
S cosφ; Q
= S sinφ.
 Произведение
комплексного напряжения
Произведение
комплексного напряжения
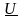 и
комплексного тока
и
комплексного тока
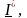 сопряженного с комплексным током
сопряженного с комплексным током
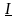 ,
называют комплексной мощностью:
,
называют комплексной мощностью:
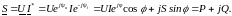
1.4 Основы комплексного метода
Комплексный (символический) метод использует замену операций с синусоидальными функциями времени действиями над изображающими их комплексными числами и базируется на следующих ниже теоремах.
Пусть мгновенному значению тока
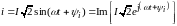
соответствует комплексное действующее значение
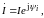
тогда справедливы нижеследующие положения.
Теорема линейности: линейной комбинации синусоид соответствует такая же комбинация изображающих их комплексов

Иными словами, сумме синусоид соответствует сумма изображающих их комплексов, умножению синусоиды на постоянное число – умножение комплекса на то же самое число.
Теорема дифференцирования: операции дифференцирования синусоиды по времени соответствует умножение изображающего ее комплекса на j, т. е.
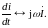
Теорема
интегрирования: операции
интегрирования синусоиды по времени
соответствует деление изображающего
ее комплекса на
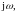 т. е.
т. е.
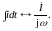
1.5 Законы ома и кирхгофа в комплексной форме
В соответствии со свойством линейности законы Кирхгофа применительно к синусоидальному режиму работы цепи можно переписать в комплексной форме следующим образом.
Первый закон. Алгебраическая сумма комплексных токов в узле равна нулю.
Второй закон. Алгебраическая сумма комплексных падений напряжения в контуре равна алгебраической сумме комплексных ЭДС.
Или:
для узла

для
контура
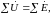
причем в понятие «алгебраическая» вкладывается тот же смысл, что и для мгновенных значений величин.
Закон Ома в комплексной форме получается в результате применения всех вышеприведенных теорем к последовательному и параллельному соединению элементов R, L, C (фактически он уже получен выше без строгих доказательств):

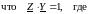
![]()
Отсюда легко получаются формулы для определения параметров двух эквивалентных схем замещения пассивного двухполюсника.
Добавим к этим формулам понятие комплексной мощности
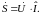
Если
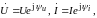 то сопряженный комплекс тока
то сопряженный комплекс тока
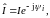 тогда
тогда
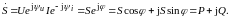
Сравнивая приведенные в этом разделе формулы с формулами, связывающими постоянные токи, напряжения и мощности, увидим, что они отличаются лишь обозначениями (табл. 1.1).
Таким образом, все методы расчета, основанные на законах Кирхгофа и используемые для расчета цепей постоянного тока, применимы и к расчету цепей синусоидального тока в комплексной форме.
Таблица 1.1
|
Постоянный ток |
Синусоидальный ток |
Для узла |
|
|
Для контура |
|
|
Для пассивного двухполюсника |
U = IR RG = 1 |
|
Мощность |
|
|
1.6 Основы работы с комплексными числами в пакете MathCad
Система MathCad производит вычисления, как с действитель-ными, так и с комплексными числами, которые представляются в алгебраической форме:
z:= a+bi,
где a – реальная часть комплексного числа z,
b – мнимая часть,
i – мнимая единица (система допускает записывать так же j).
Между числовым значением мнимой части мнимой части и символом i никакого знака не ставится. Если мнимая часть б задана не числом, а идентификатором, то мнимую часть нужно писать как умноженную на 1i. Ниже (таб. 1.2) приводятся операторы для выполнения арифметических действий над комплексными числами.
Таблица 1.2
Операторы |
Набор на лавиатуре |
Назначение оператора |
|z| |
|z |
Выражение модуля комплексного z |
|
Z” |
Вычисление комплексно сопряжённого с z числа |
Встроенные функции комплексного аргумента:
Re (z) - выделение действительной части z
Im (z) - выделение мнимой части z
arg(z) - вычисление аргумента комплексного числа z.
1.7 Расчёт цепей переменного тока
В цепях переменного тока изменение во времени питающего напряжения влечёт за собой изменение тока, а также магнитного и электрического полей, связанных с цепью. Результатом этих изменений является возникновение ЭДС самоиндукции и взаимоиндукции в цепях с катушками индуктивности, а в цепях с конденсаторами появляются зарядные и разрядные токи, которые создают сдвиг по фазе между напряжениями и токами в таких цепях. При расчетах, описанные физические процессы учитывают введением реактивных сопротивлений, что усложняет расчёт цепей переменного тока, так как приходится определять не только величину тока, но и его угол сдвига по отношению к напряжению.
Все основные законы цепей постоянного тока справедливы и для цепей переменного тока, но только для мгновенных значений или значений в векторной (комплексной) форме. На основе этих законов составляют уравнения, позволяющие расчитать цепь. Как правило, целью расчёта цепи переменного тока является определение токов, напряжений, углов сдвига фаз и мощностей на отдельных участках. При составлении уравнений для расчёта таких цепей выбирают условные положительные направления ЭДС, напряжений и токов. Получаемые уравнения для мгновенных значений в установившемся режиме и синусоидальном входном напряжении будут содержать синусоидальные функции времени. Анализ цепи переменного тока упрощают, используя тот факт, что синусоидальную функцию можно условно изобразить вектором, а вектор, в свою очередь, можно записать в виде комплексного числа. Метод расчёта цепи, основанный на применении комплексных чисел, называется символическим методом или методом комплексных амплитуд. Завершают расчёт цепи переменного тока, как правило, составлением баланса активных и реактивных мощностей, который позволяет проверить правильность вычислений.
Анализ цепей методом комплексных, амплитуд содержит следующие этапы:
1) замена гармонических, токов и напряжений всех ветвей их комплексными изображениями, а эквивалентной схемы цепи для мгновенных значений – комплексной схемой замещения;
2) составление уравнений электрического равновесия цепи для комплексных изображении токов и напряжений на основе законов Ома и Кирхгофа в комплексной форме;
3) решение системы уравнений электрического равновесия относительно комплексных изображений интересующих токов и напряжений;
4) переход от комплексных изображений токов и напряжений к их оригиналам.
Пример 1.1: Вычислить эквивалентное сопротивление параллельного включения сопротивлений z1=2+3i и z2=5+10 i.
Р исунок
1.7- Параллельное соединение комплексных
сопротивлений
исунок
1.7- Параллельное соединение комплексных
сопротивлений

Пример 1.2. Расчет электрических цепей методом эквивалентных преобразований. Пусть задана электрическая цепь, изображённая на рис. 1.8. Требуется методом эквивалентных преобразований найти токи в ветвях при заданных значениях комплексных сопротивлений и ЭДС:
z1=2+3i; z2=4+5i; z3=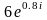 ;
;
z4=10i; z5=-8.1i; E=25.2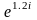 .
.
Р исунок
1.8 - Исходная схема электрической цепи.
исунок
1.8 - Исходная схема электрической цепи.
Вначале все комплексные величины, заданные в показательной форме, переведём в алгебраическую форму, в которой MathCAD производит все вычисления.
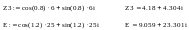
Зададим
все остальные исходные данные
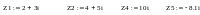
Преобразуем треугольник z2, z3, z4 в эквивалентную звезду, после чего схема приобретает более простой вид (см. рис. 1.9):
Сопротивления лучей звезды вычисляются по формулам:
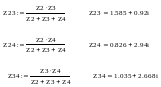
Р исунок
1.9 – Схема электрической цепи после
преобразования треугольника в звезду.
исунок
1.9 – Схема электрической цепи после
преобразования треугольника в звезду.
z5 и z24 соединены последовательно и эквивалентны сопротивления равно их сумме

z1 и z23 так же соединены последовательно:

После этих преобразований схема упрощается.

Рисунок 1.10 – Схема после упрощения
Теперь из схемы на рис. видно, что z123 и z245 соединены параллельно, следовательно, их эквивалентное сопротивление равно

Эквивалентное сопротивление относительно узлов a, b равно сумме сопротивлений z1_5 и z34:

Ток в ветви с источником найдём по закону Ома:

Напряжение между узлами a, o найдём по закону Ома

Напряжение Uob также находится по закону Ома

Токи I1 и I5 схемы рис. 1.10 найдём по закону Ома
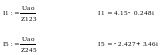
Напряжения Udo и Uco также найдём по закону Ома:
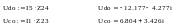
Напряжение между узлами c и d найдём как разность напряжений Uco и Udo

Напряжения между узлами c и b , а так же d и b, ищем как суммы

Теперь, когда известны напряжения между всеми узлами электрической цепи на рис. 1.10 найдём все токи исходной цепи
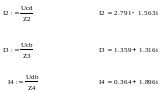
Выполним проверку по законам Кирхгофа.
Найдём погрешность по токам