2.3 Неопределенный интеграл и его свойства

Имея функцию, можно по известным правилам найти ее производную, то есть продифференцировать. Это имеет большое практическое значение: нахождение скорости, ускорения, уголовного коэффициента касательной и т.п.

Однако часто приходится решать обратную задачу: дана функция f(x), требуется найти функцию F(x) такую, что или .

Для решения обратной задачи служит операция интегрирования, обратная операции дифференцирования.

Функцию F(x) называют первообразной для f(x).

Пример 1. Найти первообразную для функции .

Такой первообразной является функция , так как . Но это не единственная первообразная для . Также подойдут: , и вообще , где С – произвольная постоянная, потому что .

Пример 2. Найти первообразную для функции .

Первообразной для функции будет , так как .

Пример 3. Найти первообразную для функции .

Первообразной для функции будет , так как .

Определение 1. Функция F(x) + C называется первообразной для функции f(x), если выполняется условие .

Определение 2. Множество первообразных F(x)+С, соответствующих данной функции f(x), называют неопределённым интегралом и обозначают символом

Можно записать: , где - подынтегральное выражение,

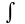- знак неопределённого интеграла,

С – постоянная интегрирования.

Основные свойства неопределённого интеграла

1. Неопределённый интеграл от дифференциала функции равен этой функции плюс произвольная постоянная

2. Постоянный множитель можно выносить за знак интеграла:

3. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от каждой из них

Таблица неопределенных интегралов

1		6
2	, если n≠1	7
3		8
4		9
5		10

Пример 1. Найти

Решение: по свойству (2) и по формуле (2) получим:

Пример 2. Найти

Решение: применяя свойства (2) и (3), затем формулы (2) и (1), получим:

Примечание. Здесь С является алгебраической суммой четырех произвольных постоянных для каждого интеграла.

Пример 3. Найти

Решение:

Проверьте себя

Выполнить интегрирование

№	Примеры	Ответы
1
2
3

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Дать определение первообразной функции

2. Что называют неопределенным интегралом?

3. Перечислите свойства неопределенного интеграла.

4. Назовите действие, обратное к дифференцированию.

2.4 Интегрирование способом подстановки

Если заданный интеграл простейшими преобразованиями трудно привести к табличному, то прибегают к особым методам. Одним из них является интегрирование способом подстановки.

Пример 1. Найти

Решение. Введём новую переменную: . Найдём дифференциал: или . Выразим . Подставим в интеграл полученные замены:

.

Проверим с помощью дифференцирования:

Получили подынтегральное выражение, значит, интегрирование было проведено верно.

Пример 2. Найти .

Решение:

Пример 3. Найти

Решение: