МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УДМУРТСКОЙ РЕСПУБЛИКИ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ УДМУРТСКОЙ РЕСПУБЛИКИ

«ИЖЕВСКИЙ ТОРГОВО-ЭКОНОМИЧЕСКИЙ ТЕХНИКУМ»

(БОУ СПО УР «ИТЭТ»)

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ДЛЯ СТУДЕНТОВ ПО ПОДГОТОВКЕ К ЗАЧЕТУ ПО ДИСЦИПЛИНЕ

МАТЕМАТИКА

ОСНОВНОЙ ПРОФЕССИОНАЛЬНОЙ ОБРАЗОВАТЕЛЬНОЙ ПРОГРАММЫ

ПО СПЕЦИАЛЬНОСТИ

100701 Коммерция (по отраслям)

(базовой подготовки)

Составила преподаватель

С.И. Ловчая

2013 г.

СОДЕРЖАНИЕ

Глава 1. Элементы линейной алгебры

1.1 Матрицы. Определители. Метод Крамера решения систем линейных уравнений.

1.2 Комплексные числа. Действия в алгебраической форме.

Глава 2. Математический анализ. Дифференцирование и интегрирование функций

2.1 Предел функции.

2.2 Производная функции. Дифференциал.

2.3 Неопределенный интеграл и его свойства.

2.4 Интегрирование способом подстановки

Глава 3. Элементы теории вероятностей и математической статистики

ВВЕДЕНИЕ

Глава 1. Элементы линейной алгебры

1.1 Матрицы. Определители. Метод Крамера решения систем линейных уравнений

Определение. Прямоугольная таблица, составленная из n ∙ m чисел:

называется матрицей из n строк и m столбцов или матрицей размера n x m, а также n x m – матрицей. Числа (i = 1, 2,…,n; j = 1, 2, …,m) называются элементами матрицы; первый индекс i элемента указывает номер строки, в которой стоит элемент матрицы, а второй индекс j – номер столбца.

Если количество строк и столбцов равно, т. е. n=m, то матрица называется квадратной.

Рассмотрим квадратную матрицу второго порядка: .

Определителем 2-ого порядка называют число:

Например, = = 5.

Рассмотрим квадратную матрицу третьего порядка:

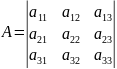
Вычисление определителя 3-его порядка осуществляется по определенному правилу:

1) создать сумму произведений элементов по одному из каждой строки и каждого столбца со знаком + или – (правило треугольников)

=

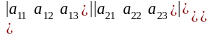Например, 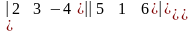= =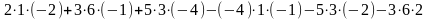 – 92.

2) разложить определитель по любой строке или любому столбцу, выводя элементы из определителя со знаком из схемы 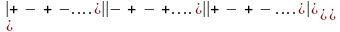(знаки чередуются), и умножая их на соответствующие каждому элементу миноры.

Минором определителя называется определитель, который получается, если удалить ту строку и тот столбец данного определителя, из которого выводится элемент.

Формула разложения определителя по первой строке:

=

Например:

= = = - 92.

Определение. Системой m линейных уравнений с n неизвестными называют систему вида:

где а_ij – коэффициенты; х_j – неизвестные. Первый индекс i – означает номер строки, второй j – номер столбца. В случае, когда система не высокого порядка, можно коэффициенты и неизвестные обозначать разными буквами.

Рассмотрим систему трех линейных уравнений с тремя неизвестными:

,

где а₁, а₂, a₃, b₁, b₂, b₃, c_1, c₂, c₃, d₁, d₂, d₃ – коэффициенты; х, у, z – неизвестные.

Определение. Тройка чисел (х₀ , у₀ , z₀ ) называется решением системы, если при подстановке этих чисел в уравнение системы вместо х, у, z получаются верные числовые равенства.

Метод Крамера

Метод Крамера состоит в следующем. Составляется n + 1 определитель:

Δ – определитель системы (составляется из коэффициентов системы в том порядке, как они записаны в системе;

Δ_хi – определители каждого неизвестного (составляются из определителя системы Δ путем последовательной замены столбца коэффициентов того неизвестного, определитель которого записывается, столбцом свободных коэффициентов)

Решение системы находится по формулам Крамера:

х₁ = ; х₂ = ; … х_n = .

Если Δ = 0, то система либо не имеет решений, либо имеет бесконечное множество решений, которые могут быть найдены методом исключения.

Пример 1. Решить методом Крамера:

Решение. Составим и найдем определитель системы:

Δ = = -12-10= -22

Составим и найдем определитель Δх (заменим столбец коэффициентов при неизвестном х столбцом свободных коэффициентов):

Δх = = -56+100= 44

Найдем определитель Δу (заменим столбец коэффициентов при неизвестном у столбцом свободных коэффициентов):

Δу = = - 60-28= -88

Решением будет: 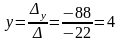. Ответ: (-2; 4).

Пример 2. Решить систему методом Крамера: .

Решение. Составим и найдем определитель системы:

Δ = = - 27

Составим и найдем определитель Δх (заменим столбец коэффициентов при неизвестном х столбцом свободных коэффициентов):

Δх = = - 81

Вернем первый столбец на место и составим и найдем определитель Δу (заменим столбец коэффициентов при неизвестном у столбцом свободных коэффициентов):

Δу = = - 108

Вернем второй столбец на место и составим и найдем определитель Δz (заменим столбец коэффициентов при неизвестном z столбцом свободных коэффициентов):

Δz = 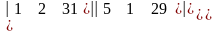= - 135.