
- •Примеры к контрольной работе № 1а
- •Задания к контрольной работе № 2
- •Контрольная работа № 1б
- •Примеры нахождения производных
- •Задания к контрольной работе № 1б
- •Контрольная работа № 1в Исследование функций с помощью производных.
- •2 Контрольных задания.
- •Примеры решения заданий контрольной работы №1в
- •Задания к контрольной работе №1в
- •Контрольная работа № 1г
- •Теория определителей и векторной алгебры»
- •Решение некоторых типовых примеров и методические указания по контрольной работе
- •Задания к контрольной работе № 1г
- •Контрольная работа № 1д
- •Примеры к контрольной работе № 1д
- •Задания к контрольной работе № 1д
- •Литература
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГЕОЛОГОРАЗВЕДОЧНЫЙ
УНИВЕРСИТЕТ
Кафедра математики
Методические указания и задания
к контрольным работам студентов
I курса заочного отделения
(для ЗПМ)
Составители: Ваксман К.Г.
Михайлова А.В.
Москва,
2011 г.
Контрольная работа № 1а
Тема: «Пределы и непрерывность»
Основные теоретические сведения
(см. «Методические указания»)
Символика
с – постоянная
![]()
![]() (неопределенность);
(неопределенность);
![]() (неопределенность).
(неопределенность).
Бесконечно-малые и бесконечно-большие функции
Функция
![]() называется бесконечно-малой
(бесконечно-большой) при
называется бесконечно-малой
(бесконечно-большой) при
![]() ,
если
,
если
![]() (
(![]() ).
).
Предел отношения двух многочленов

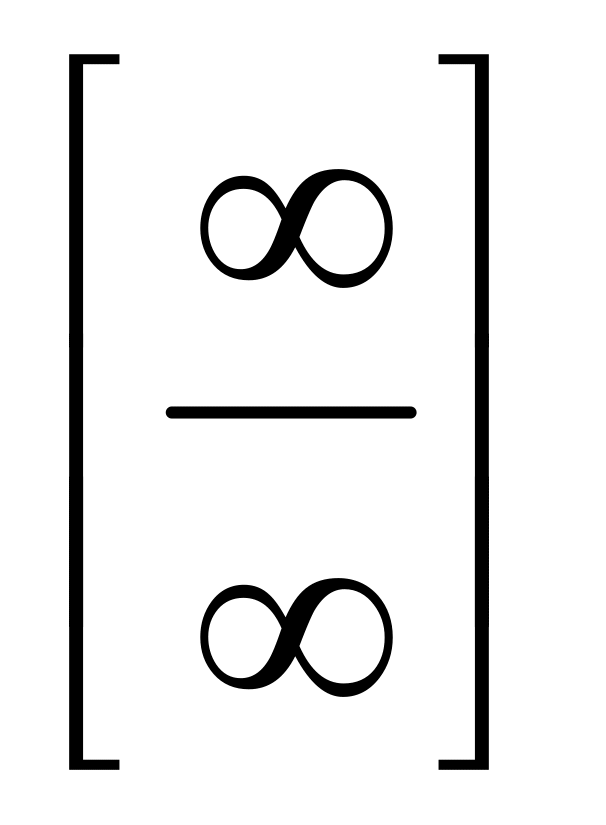 .
Для раскрытия неопределенности
числитель и знаменатель требуется
разделить на
.
Для раскрытия неопределенности
числитель и знаменатель требуется
разделить на
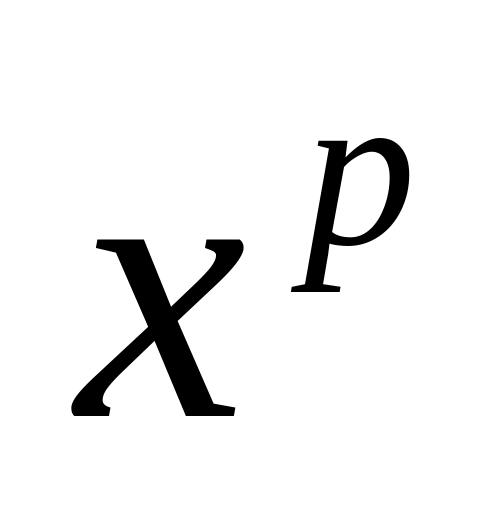 ,где
,где
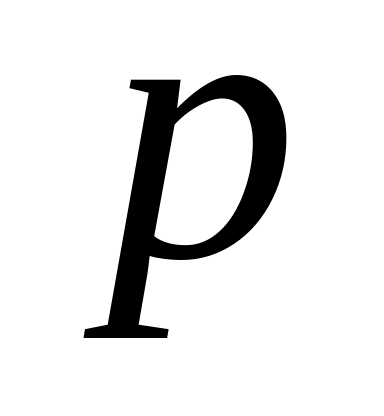 -
наибольший показатель степени при
-
наибольший показатель степени при
 в числителе и знаменателе. Затем
использовать, что
в числителе и знаменателе. Затем
использовать, что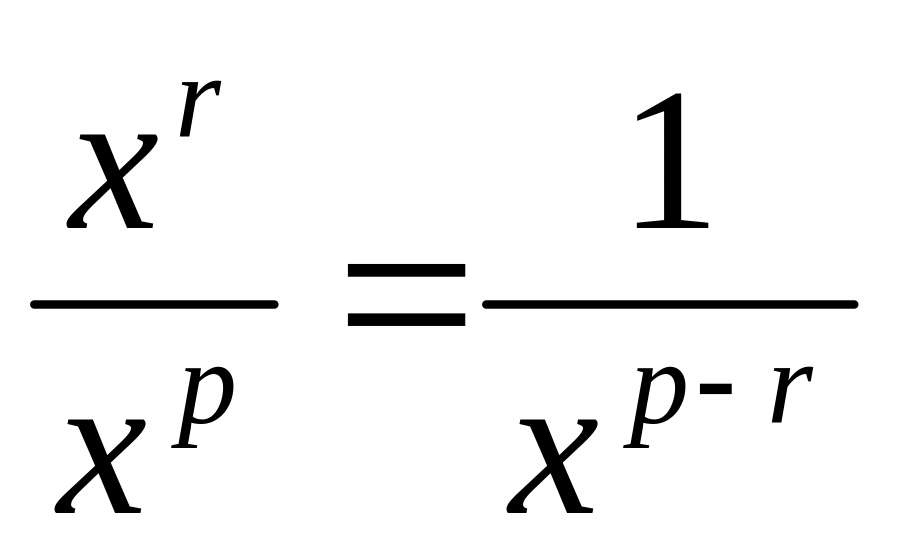 и
и

 при
при
 .
.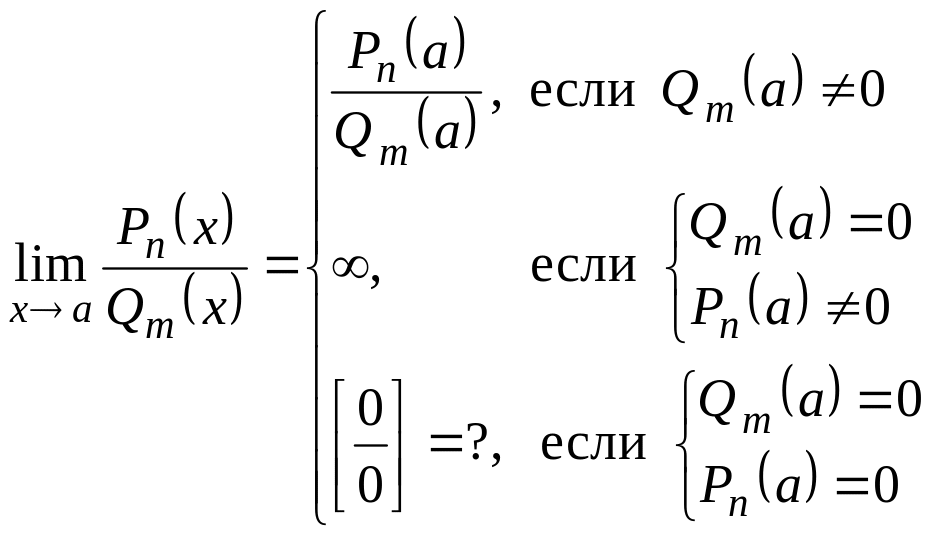
Для раскрытия неопределенности
![]() числитель и знаменатель требуется
разложить на множители и сократить на
общий множитель
числитель и знаменатель требуется
разложить на множители и сократить на
общий множитель
![]() .
Использовать формулы:
.
Использовать формулы:
![]() ;
;
![]()
![]() ,где
,где![]() и
и![]() –корни,
–корни,
![]() ,
,
![]() ;
;
Первый замечательный предел
![]()
![]() при
при
![]() .
Следствие:
.
Следствие:
![]() ,
так как
,
так как
![]() .
.
Сделав замену переменной
![]() получим
получим
![]() ,
аналогично:
,
аналогично:
![]() .
.
Использовать формулы:
![]() ;
;
![]() ;
;
![]() .
.
Второй замечательный предел
![]() ;
;
![]() .
Число
.
Число![]()
Функция
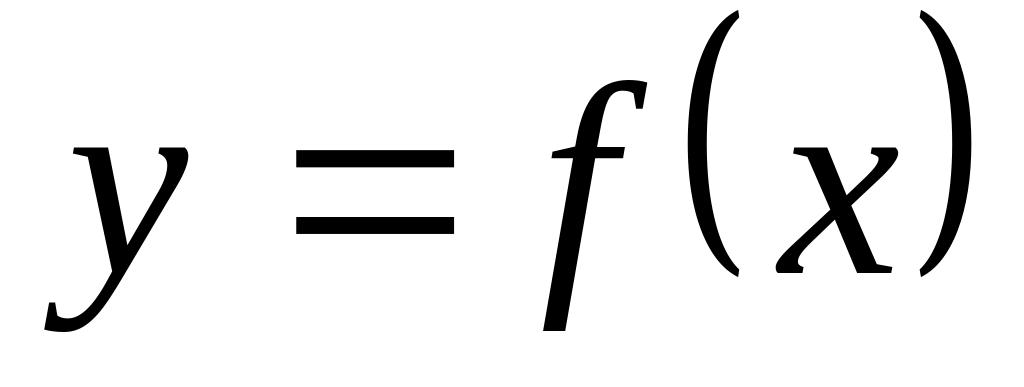 называется непрерывной в точке
называется непрерывной в точке
 ,
если
,
если
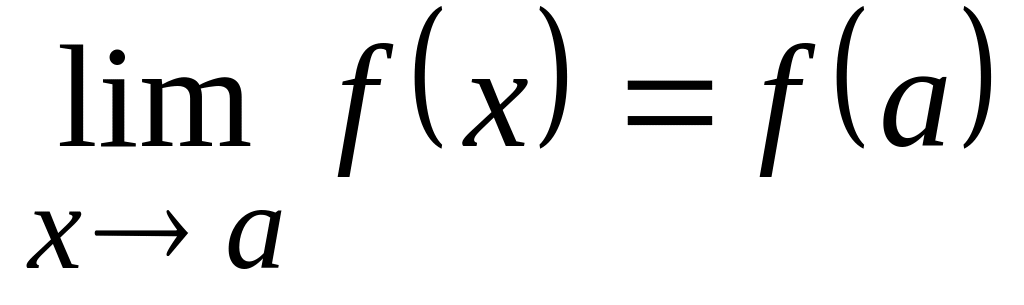 .
.
Условия непрерывности функции в точке :
функция должна быть определена в некотором интервале, содержащем точку а (т.е. в самой точке и вблизи этой точки);
функция должна иметь одинаковые односторонние пределы:
![]() ;
;
эти односторонние пределы должны быть равны
 .
.
Примеры к контрольной работе № 1а
Какие из следующих функций являются бесконечно малыми, бесконечно большими при
 (правило 2):
(правило 2):
а)
 ;
;
![]()
имеет конечный предел при
![]() .
.
б)
![]()
![]() является бесконечно большой при
.
является бесконечно большой при
.
в)
![]()
![]() является бесконечно малой при
является бесконечно малой при
![]() .
.
Найти пределы функций. Пользуемся правилами 1, 2, 3, 4, 5.
а)

 ,так
как
,так
как
![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() .
.
б)
 .
.
При этом разложим квадратный трёхчлен в числителе на множители
,
где
и
– корни,
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
В знаменателе
![]() ,
т.к.
.
,
т.к.
.
в )
)
![]() =
Пусть
=
Пусть
![]() ,
,
![]() ,
,
![]() =
=
![]() .
.
г
)
![]() Пусть
Пусть
![]() ,
,
,
,
![]() =
=
![]() .
.
Задана функция
 .
Найти точки разрыва функции, если они
существуют. Сделать чертёж.
.
Найти точки разрыва функции, если они
существуют. Сделать чертёж.
![]()
– определена и непрерывна на всей
числовой оси. Она может иметь разрывы
в точках
![]() и
и
![]() .
Найдем односторонние пределы (слева и
справа) в этих точках.
.
Найдем односторонние пределы (слева и
справа) в этих точках.
y
3
2
1
1 2 x
Чертёж






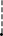

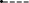
 ;
;
![]() ;
;
![]() ;
;
![]() .
Левый и правый пределы конечные, но не
равны между собой;
.
Левый и правый пределы конечные, но не
равны между собой;
![]() имеет в точке
конечный разрыв скачок равен
имеет в точке
конечный разрыв скачок равен
![]() .
.
;![]() ;
;
![]() ;
;![]() .Пределы
слева и справа конечны и равны
.Пределы
слева и справа конечны и равны
![]() .
В точке
–
непрерывна.
.
В точке
–
непрерывна.
Задания к контрольной работе № 2
Содержит 3 контрольных задания:
Какие из следующих функций являются бесконечно малыми и бесконечно большими при .
Найти пределы функции.
Задана функция . Найти точки разрыва функции, если они существуют. Сделать чертеж.
№ вар-та |
Задания |
№ вар-та |
Задания |
1 |
1) а)
в)
2) а)
в)
3) |
2 |
1) а)
в)
2. а)
в)
3)
|
3 |
1) а)
в)
2) а)
в)
3)
|
4 |
1) а)
в)
2) а)
в)
3)
|
5 |
1) а)
в)
2) а)
в)
3)
|
6 |
1) а)
в)
2) а)
в)
3)
|
7 |
1) а)
в)
2) а)
в)
3)
|
8 |
1) а)
в)
2) а)
в)
3)
|
9 |
1) а)
в)
2) а)
в)
3)
|
0 |
1) а)
в)
2) а)
в)
3)
|

 ;
б)
;
б)
 ;
;
 ;
б)
;
б)
 .
. ;
б)
;
б)
 ;
б)
;
б)
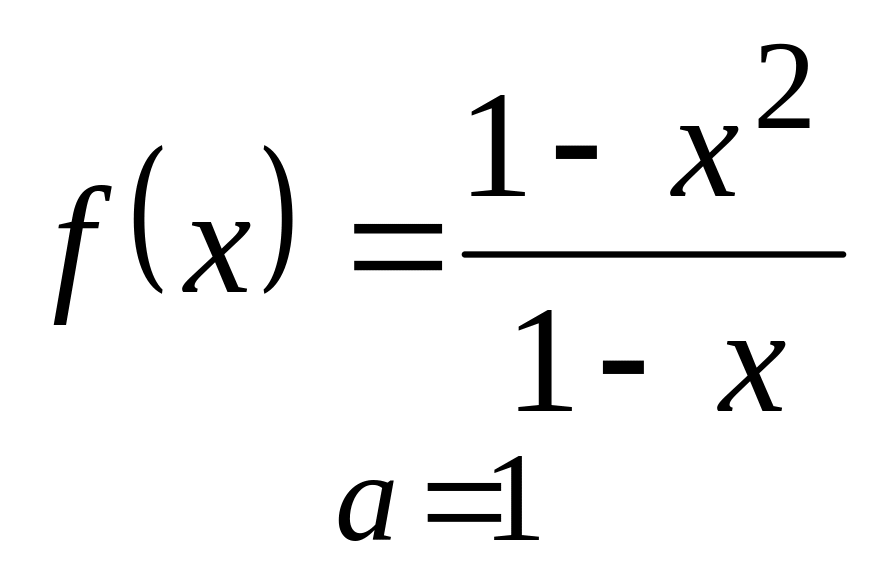 ;
;
 .
. ;
б)
;
б)
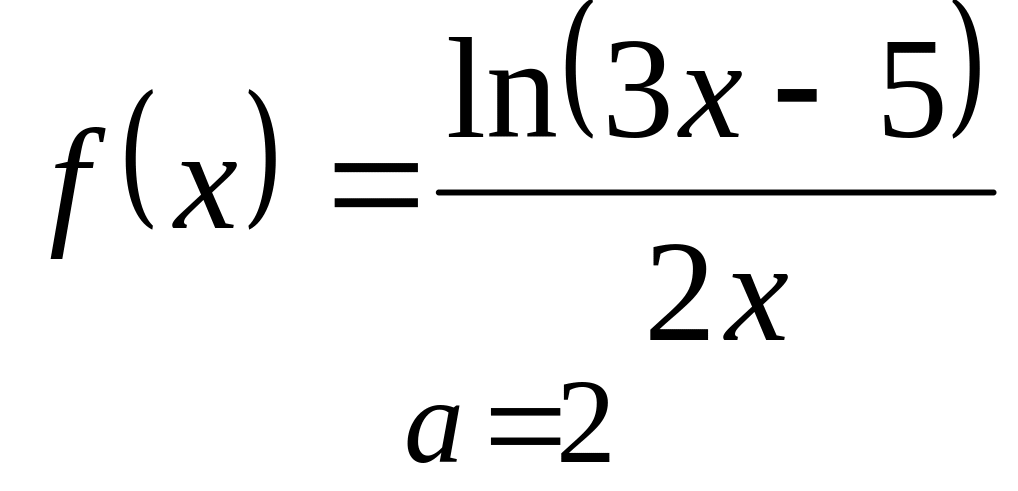 ;
;
 .
. ;
;
 ;
б)
;
б)
 .
. ;
;
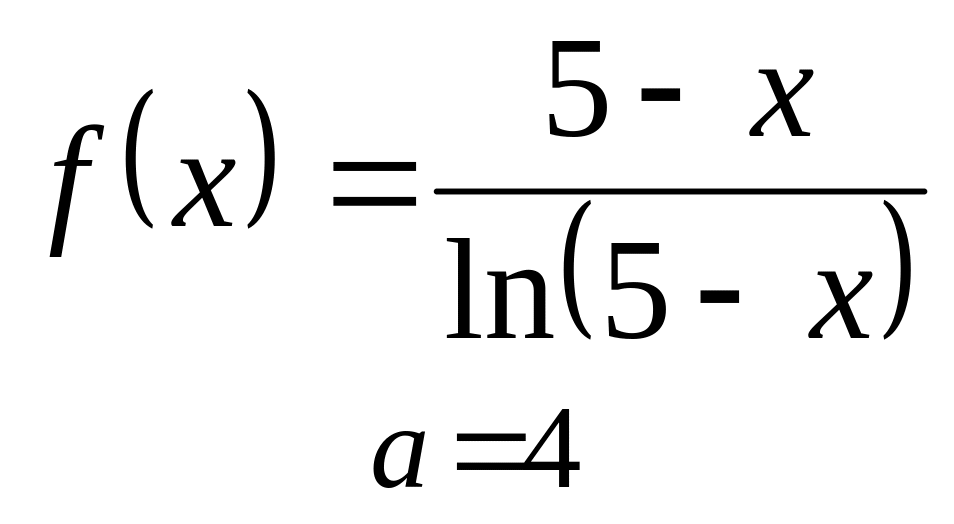 .
. ;
;
 .
.