Р ешение
Сделаем чертежи и рассмотрим равновесие каждого тела [1] П 14-17. Выберем оси координат и составим уравнения равновесия для стержня АВ (рис. 1.2).
(1.2)
.
В систему уравнений (1.2) входят три неизвестные реакции: ХА, УА и NC, и мы можем однозначно определить их значения.
Выберем оси координат и составим уравнения равновесия для стержня СD (рис. 1.3).
;
(1.3) 
.
Из этих уравнений определяются последние три неизвестные реакции ХD, YD, NE.
Таким образом, для конструкции, состоящей из двух твердых тел, можно составить шесть уравнений равновесия. Для данной задачи оптимальными являются уравнения (1.2) и (1.3), из которых находятся все внешние и внутренние реакции.
Пример.2
Дано: На рис1.5 изображена схема устройства, равновесие которого нужно рассмотреть и определить силы реакций опор А, В и С, если Р=6 кН; Q=10 кН; F=8 кН; М=24 кН·м; q=2кН/м; АD=DС=CK=1м.
Решение. Рассмотрим равновесие стержня ВК (рис.1.6)
Рис.1 .5
Рис. 1.6
Составим три уравнения равновесия:
;
ХB
+ RC1·Cos30°
+ RC2·Sin30°
– P·Cos20°
= 0 (1.4)
;
YB
– RC1·Sin30°
+ RC2·Cos30°
– P·Sin20° = 0 (1.5)
;
M – RC2·BC
– P·BK·Sin50° = 0 (1.6)
Из
уравнения (1.6) находим:
Теперь рассмотрим равновесие стержня АС. Составим три уравнения равновесия Рис.1.8
;
ХА
– RC1·Cos30°
– RC2·Sin30°
= 0(1.7)
; YA + RC1·Sin30° – RC2·Cos30° – Q = 0 (1.8)
Рис.1.8
– RC2·Sin30°·AC = 0 (1.9)
Из уравнения (1.9) находим:
Из уравнения (1.4) находим:
Из уравнения (1.5) находим:
Из уравнения (1.7) находим:
Из уравнения (1.8) находим:
Ответ: ХА= 9,44 кН; YА= 10,45 кН; RС1= 7,95 кН
ХВ= –3,80 кН; YВ= 1,60 кН; RС2= 5,11 кН
;
Задание с 2. Равновесие вала с закрепленными на нем телами
Рассмотреть равновесие пространственной конструкции, которая имеет ось вращения АВ. Определить реакции опор и значение неизвестной силы. В тех вариантах, где на тело действуют силы t и T, учесть, что T = 2t.
Варианты
1. 2.
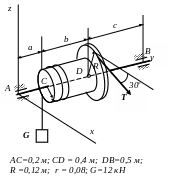
3
.
4.
6. z 5
7. 8.
9. 10.
1
z
a
b
c
T
B
A
30o
y
D
С
R
r
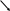
G
x
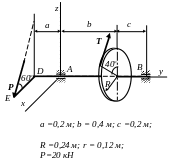
a =0,4 м;
b = 0,4м; c =0,6м;
R=0, 18м; r = 0,15м;
G=100кН
z
1
D
3
14.
y
A
C
D1
P
x
B
C1
30o
AD = AD1; P=20кН
15 16.
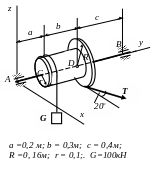
y
1
7.
18.
P=16 кН
1
z
9.
20.
a
b
c
30o
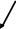
B
A
r
R
E
y
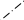
C
D
T
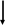
G
x
P
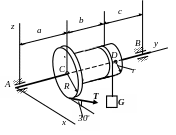
a =0,4 м;
b = 0,4м; c = 0,6м;
R
=0, 18м; r = 0,15;
P=100кН; G=60кН.
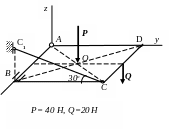
AD = AD1; P=24кН;
Q=20кН
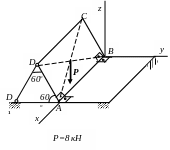
21. 22.
Р=40кН
a =0,2 м;
b = 0,4м; c = 0,3м;
R
=0, 2м; r = 0,12; Р=100кН
23. 24.
25
26
2
7.
28.
29. 30.
a =0,2 м; b
= 0,4 м; c=0,2 м;
R
=0, 2 м; r = 0,15
м; Р=20 кН
3
1.
32.
y
33. 34.
a =0,4 м; b
= 0,3 м; c=0,3 м;
R=0,2
м; r=0,18 м; Р=20 кН
35. 36.
x
.
3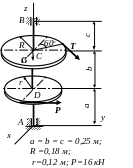
7.
38.
3
9.
40.
y
ВС= BC1
, P=100кН
a =0,2 м;
b = 0,4 м; c = 0,4 м;
R=0,2
м; r=0,15 м;
G=10 кН
4
1.
42.
4
3.
44.
45. 46.
4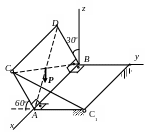
7.
48.
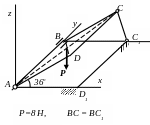
AC = AC1,
Р=6 Н=ЗХхЗЗзз
4
y
C1
60o
C
z
D1
D
y
B
30o
P
А
x
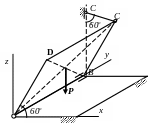
CA = AD = DB = 0,4 м;
R
=0,2 м; r = 0,12 м;
Р=20 кН
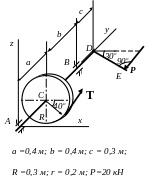
Р=12 Н
5
1.
52.
X
55. 56.
AC = CD = DB = 0,4 м;
R
=0,2 м; r = 0,16
м; Р=20 кН
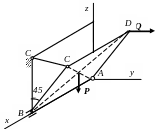
57. 58.
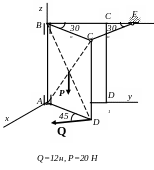
BC = BC1,
Р=10 Н, Q= 20 Н, Сила
Q параллельна оси
Ax.
a =0,2 м; b
= 0,2 м; c =
0,5 м;
R=0,3
м; r=0,15 м; Р=20 кН
59. 60.
6
1.
62.
63. 64.
x
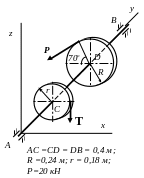65.
66.
67. 68.
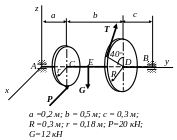
a =0,2 м;
b = 0,1 м; c = 0,3 м;
R=0,24
м; r=0,18 м;
G=12 кН
6
z
9.
70.
71.
72.
7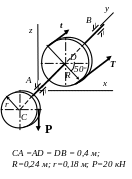
3.
74.
7
5.
76.
77.
78.
a =0,6 м;
b = 0,4 м;
R
=0, 24 м; r = 0,12 м; Р=20
кН
79.
80.
8
1.
82
.
8
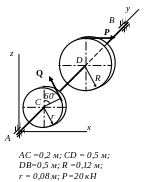
3.
84.
BE = EC, Р=30 Н
8
5.
86.
x
8
7.
88.
8
9.
90.
9
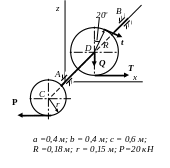1.
92.
93. 94.
9
5.
96.
C1
9
7.
98.
99. 100.
x
Пример. Равновесие вала с закрепленными на нем телами
Н
Q
Определить вес груза Q, если вал остается в равновесии, а также реакции подшипников А и В, пренебрегая весом вала.
Р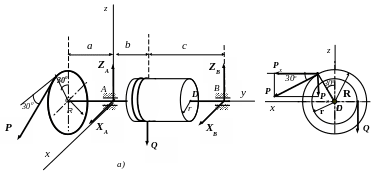
ешение.
Рассмотрим
равновесие вала с закрепленными на нем
телами, сделаем чертеж (рис.1.10a).
На вал действуют активные силы –
натяжения нитей Р
и Q,
направленные по касательным к окружностям
колеса и ворота и, следовательно,
расположенные в плоскостях, перпендикулярных
оси y.
Рис. 1.10
b)
Реакцию каждого подшипника раскладываем на две взаимно перпендикулярные составляющие: XA, ZA и XB, ZB, лежащие в плоскости, перпендикулярной оси вращения вала. Начало координат выбираем в точке А. Направим ось у по оси вала, ось z – вертикально, ось х – так, чтобы получить правую систему декартовых координат.
Неизвестными являются реакции XA, ZA, XB, ZB и сила натяжения Р. В данной системе можно составить пять уравнений равновесия (сумма проекций всех сил на ось у равна нулю), поэтому задача является статически определенной [1] П 28,30.
Сделаем дополнительный чертеж, представляющий собой вид на барабан и колесо с конца оси вала – оси у (рис. 1.10b). Составим уравнения равновесия:
Из этих уравнений однозначно определяются все неизвестные.