
- •Основные определения и понятия.
- •Задание по расчету электростатического поля.
- •2. Задание по расчету электрического поля постоянного тока.
- •3. Задание по расчету магнитного поля постоянного тока.
- •4. Задание по расчету электрического поля путем составления интегрального уравнения и его приближенного решения.
4. Задание по расчету электрического поля путем составления интегрального уравнения и его приближенного решения.
А) расчет электрического поля в диэлектрике.
Задача 1. В диэлектрике
с известной относительной диэлектрической
проницаемостью среды
![]() в плоскости рисунка (рис. 14 или рис. 15
согласно варианту задания) находятся
два одинаковых цилиндрических электрода.
Длина электродов
в плоскости рисунка (рис. 14 или рис. 15
согласно варианту задания) находятся
два одинаковых цилиндрических электрода.
Длина электродов
![]() ,
расстояние
,
расстояние
![]() ,
радиус сечения
,
радиус сечения
![]() заданы, при этом
заданы, при этом
![]() ,
,
![]() .
Электрод А имеет потенциал
.
Электрод А имеет потенциал
![]() ,
электрод В – потенциал
,
электрод В – потенциал
![]() .
.
Требуется:
1) составить интегральное уравнение,
которому подчиняется линейная плотность
заряда
![]() на электроде А и аналогичное уравнение
для электрода В; 2) для приближенного
решения интегральных уравнений по п. 1
разделить каждый электрод на три участка
одинаковой длины с неизвестными
на электроде А и аналогичное уравнение
для электрода В; 2) для приближенного
решения интегральных уравнений по п. 1
разделить каждый электрод на три участка
одинаковой длины с неизвестными
![]() .
Составить систему алгебраических
уравнений для определения всех
.
Составить систему алгебраических
уравнений для определения всех
![]() .
Определить коэффициенты этой системы
и, решив ее, найти закон распределения
линейной плотности заряда вдоль оси
электрода А. Вычислить емкость между
электродами.
.
Определить коэффициенты этой системы
и, решив ее, найти закон распределения
линейной плотности заряда вдоль оси
электрода А. Вычислить емкость между
электродами.
Исходные данные для решения задачи приведены в таблице.
|
Параметр |
Варианты задания |
|||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
Рисунок |
14 |
15 |
14 |
15 |
14 |
15 |
14 |
15 |
14 |
15 |
|
|
0,5 |
1,0 |
1,5 |
2,0 |
2,5 |
0.75 |
1,25 |
1,75 |
2,25 |
2,75 |
|
|
60 |
120 |
180 |
240 |
300 |
90 |
150 |
210 |
270 |
330 |
|
|
10 |
20 |
30 |
40 |
50 |
15 |
25 |
35 |
45 |
55 |
|
|
1 |
2 |
2,5 |
4 |
5 |
1 |
2 |
2,5 |
4 |
5 |
|
|
100 |
50 |
40 |
25 |
20 |
100 |
50 |
40 |
25 |
20 |
Б) Расчет электрического поля в проводящей среде.
Задача 2. Стальная
цилиндрическая труба длиной
![]() ,
диаметром 2
,
диаметром 2![]() помещена в слабо проводящую среду
(землю). Удельная проводимость земли
помещена в слабо проводящую среду
(землю). Удельная проводимость земли
![]() много меньше проводимости трубы
много меньше проводимости трубы
![]() .
По трубе в землю стекает ток I,
который подводится к трубе по изолированному
проводу. Положение трубы в земле указано
на разрезе согласно рисунку (рис. 16 или
рис. 17 в зависимости от варианта задания).
.
По трубе в землю стекает ток I,
который подводится к трубе по изолированному
проводу. Положение трубы в земле указано
на разрезе согласно рисунку (рис. 16 или
рис. 17 в зависимости от варианта задания).
Требуется:
1) составить и решить систему интегральных
уравнений относительно линейных
плотностей токов
![]() ,
разбив предварительно трубу на три
участка одинаковой длины с неизвестными
,
разбив предварительно трубу на три
участка одинаковой длины с неизвестными
![]() ;
2) определить потенциал
;
2) определить потенциал
![]() и сопротивление растекания заземлителя
(трубы)
и сопротивление растекания заземлителя
(трубы)
![]() .
.
Исходные данные для решения задачи приведены в таблице.
|
Параметр |
Варианты задания |
|||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
Рисунок |
16 |
17 |
16 |
17 |
16 |
17 |
16 |
17 |
16 |
17 |
|
|
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
|
|
250 |
500 |
300 |
600 |
350 |
700 |
400 |
450 |
550 |
600 |
|
|
- |
40 |
- |
50 |
- |
60 |
- |
40 |
- |
50 |
|
I, А |
50 |
100 |
60 |
120 |
70 |
140 |
80 |
90 |
160 |
180 |
Рисунки к задачам.
Первая группа задач – расчет электростатического поля.
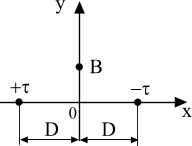
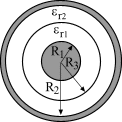
Рис. 1. Рис. 2

Рис. 3 Рис. 4
Вторая группа задач - расчет электрического поля постоянного тока.
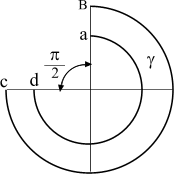
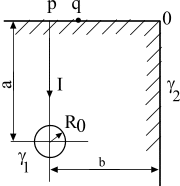
Рис. 5 Рис. 6
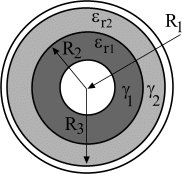
Рис. 7 Рис. 8
Третья группа задач – расчет магнитного поля постоянного тока.
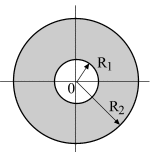
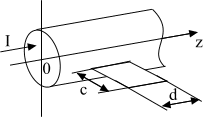
Рис. 9 Рис. 10

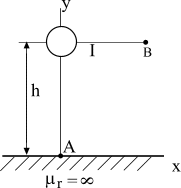
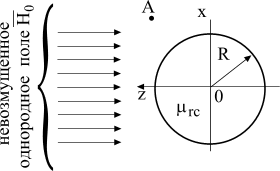
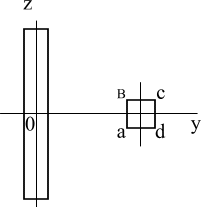
Рис. 13
Четвертая группа задач – расчет электрического поля путем составления
интегрального уравнения и его решения.
А) Расчет электрического поля в диэлектрике.
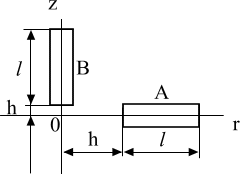
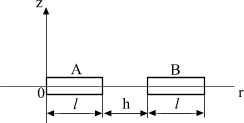
Рис. 14 Рис. 15
Б) Расчет электрического поля в проводящей среде.
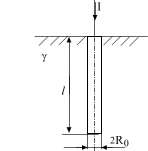
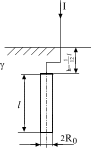
Рис. 16 Рис. 17
Примеры решения задач.
Электростатическое поле.
Пример 1. В
равномерное электрическое поле (рис.
18) с напряженностью
Требуется:
1) определить напряженность элек-трического
поля вокруг цилиндра, ее максимальное
значение с указанием координаты данной
точки поля; 2) найти плотность зарядов,
индуцированных на поверхности цилиндра.
Указание. При
решении задачи воспользоваться методом
разделения переменных.
![]() В/м внесен длинный металлический цилиндр
радиусом
В/м внесен длинный металлический цилиндр
радиусом
![]() см.
Окружающей средой является воздух
(проницаемость
см.
Окружающей средой является воздух
(проницаемость
![]() ).
).
Рис. 18
Решение.
Уравнение Лапласа в цилиндрической системе координат для определения электрического потенциала имеет вид:
![]() ,
,
Решение этого
уравнения будем искать в виде произведения
двух функций, одна из которых зависит
только от координаты r,
а другая – только от координаты
![]() :
:
![]()
Чтобы определить
функции
![]() ,
подставим искомое решение в дифференциальное
уравнение:
,
подставим искомое решение в дифференциальное
уравнение:
![]() .
.
Умножим обе части
равенства на выражение
![]() ,
получим
,
получим
![]() .
.
Равенство это
должно быть справедливым при любых
значениях r
и
![]() .
Это возможно лишь в том случае, когда
каждая из частей уравнения равна
некоторой постоянной
.
Это возможно лишь в том случае, когда
каждая из частей уравнения равна
некоторой постоянной
![]() ,
то есть
,
то есть
![]() ,
,
![]() .
.
В рассматриваемой
задаче искомое решение будет
![]() ,
причем постоянная
,
причем постоянная
![]() должна быть равна 1. В этом легко убедиться
подстановкой
должна быть равна 1. В этом легко убедиться
подстановкой
![]() в уравнение, записанное относительно
функции
в уравнение, записанное относительно
функции
![]() .
Тогда уравнение для определения функции
.
Тогда уравнение для определения функции
![]() примет вид:
примет вид:
![]() .
.
Для решения этого уравнения введем новую независимую переменную w так, чтобы
![]()
![]()
![]()
![]() .
.
Тогда
![]()
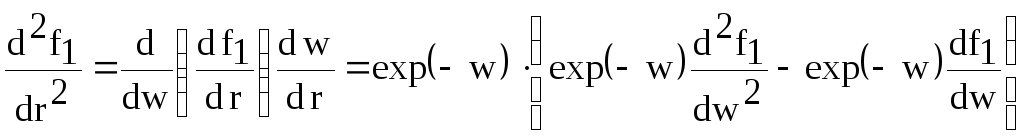 .
.
Подставив эти производные в решаемое уравнение, получим:
![]()
Общий интеграл этого уравнения имеет вид:
![]() .
.
Корни характеристического
уравнения
![]() равны
равны
![]()
![]()
Таким образом, искомый интеграл
![]()
Найдем напряженность поля
![]() ,
,
где
![]() ,
,
![]() ,
,
![]()
Соответственно проекции вектора электрического смещения
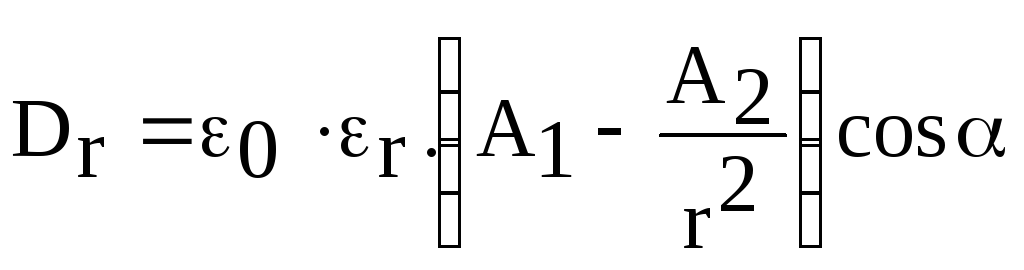 ,
,
 ,
,
![]()
Для определения
постоянных интегрирования учтем
граничные условия. При устремлении
радиуса к бесконечности
![]() влияние цилиндра не сказывается, поэтому
влияние цилиндра не сказывается, поэтому
![]() и, следовательно,
и, следовательно,
![]() или
или
![]() ,
откуда
,
откуда
![]() Поверхность цилиндра является
эквипотенциальной. При радиусе
Поверхность цилиндра является
эквипотенциальной. При радиусе
![]() потенциал
потенциал
![]() для всех значений
для всех значений
![]() ,
что возможно при условии
,
что возможно при условии
![]()
Следовательно
![]() .
Подставив значения постоянных
интегрирования, получим:
.
Подставив значения постоянных
интегрирования, получим:
![]() ,
,
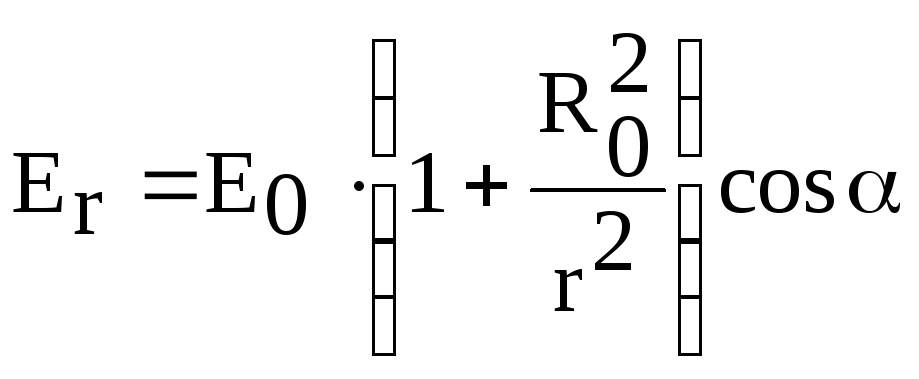 ,
,
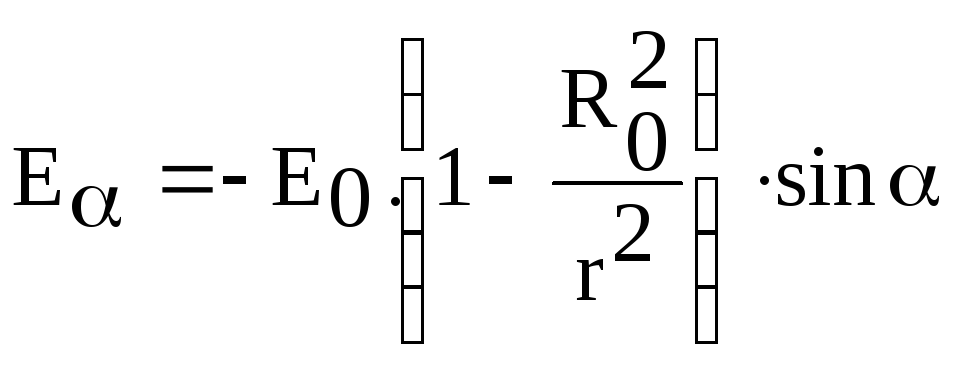 ,
,
![]() .
.
Наибольшая
напряженность
![]() будет в точке с координатами
будет в точке с координатами
![]() .
С учетом исходных данных
.
С учетом исходных данных
![]() В/м.
В/м.
Плотность зарядов, индуцированных на поверхности цилиндра:
![]() .
.
Подставляя числовые
значения в выражение плотности зарядов
![]() ,
найдем
,
найдем
![]() Кл/м.
Кл/м.
Электрическое поле постоянного тока.
Пример 2. В
цилиндрическом конденсаторе с
несовершенной изоляцией вследствие
неравномерного нагрева относительная
диэлектрическая проницаемость меняется
по закону
![]() ,
а удельная проводимость меняется по
закону
,
а удельная проводимость меняется по
закону
![]() ,
где
,
где
![]()
![]() См/м,
См/м,
![]() .
Радиус внутреннего цилиндра равен
.
Радиус внутреннего цилиндра равен
![]() м,
радиус внешнего цилиндра
м,
радиус внешнего цилиндра
![]() м.
Длина конденсатора
м.
Длина конденсатора
![]() м.
Конденсатор включен под постоянное
напряжение
м.
Конденсатор включен под постоянное
напряжение
![]() кВ.
кВ.
Требуется: 1) определить закон распределения объемного заряда в функции от расстояния до оси цилиндра; 2) вычислить ток утечки.
Решение.
В цилиндрическом
конденсаторе вектор напряженности
электрического поля
![]() ,
а следовательно, и вектор плотности
тока утечки
,
а следовательно, и вектор плотности
тока утечки
![]() будут
направлены по радиусам. Выражая
напряженность электрического поля
через ток утечки I,
найдем
будут
направлены по радиусам. Выражая
напряженность электрического поля
через ток утечки I,
найдем
![]() .
.
Напряжение между электродами
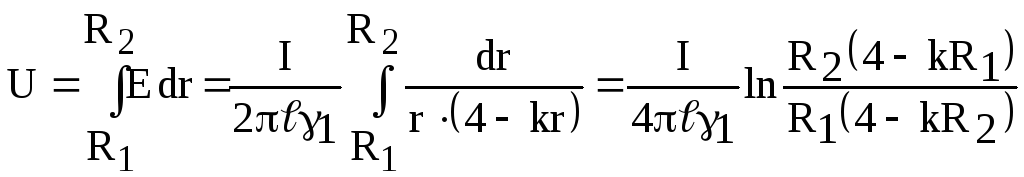 .
.![]()
Решив это уравнение относительно тока, определим
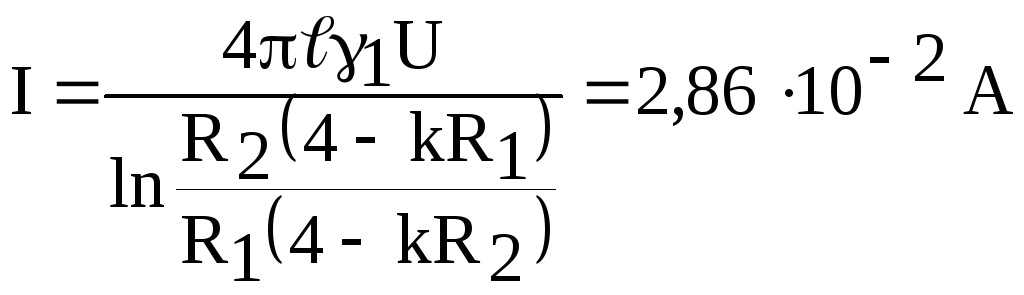 .
.
Закон распределения плотности тока:
![]()
Закон изменения напряженности электрического поля:
![]() .
.
Закон распределения объемного заряда:
![]() .
.
Так как
![]() и
и
![]() зависят только от координаты r,
то можно записать
зависят только от координаты r,
то можно записать
![]() ;
;
![]() .
.
Используя полученные выражения, окончательно найдем закон распреде-ления объемной плотности заряда
![]() .
.
Магнитное поле постоянного тока.
Пример 3. Двухпроводная
линия (рис. 19) состоит из цилиндрических
проводов с радиусом
![]() .
Расстояние между осями проводов
.
Расстояние между осями проводов
![]() .
В проводах линии протекает ток
.
В проводах линии протекает ток
![]() А. Окружающая среда воздух (относительная
магнитная проницаемость среды
А. Окружающая среда воздух (относительная
магнитная проницаемость среды
![]() ).
).
Требуется:
1) определить скалярный магнитный
потенциал для точки M,
находящейся на расстояниях
![]() от осей проводов; 2) вектор магнитной
индукции
от осей проводов; 2) вектор магнитной
индукции
![]() ,
вектор напряженности магнитного поля
,
вектор напряженности магнитного поля
![]() ,
векторный магнитный потенциал
,
векторный магнитный потенциал
![]() .
.
Указание. Влиянием земли и токами в других проводниках можно пренебречь.
Решение. При
условии
![]() расчет магнитного поля вне проводов
можно вести при допущении, что токи
проходят в бесконечно тонких нитях,
совпа-дающих с геометрическими осями
проводов. Поместим начало координат в
точку О, лежащую в середине линии,
соединяющей оси проводов (рис.19).
Скалярный магнитный потенциал в точке
М, обусловленный током в левом проводе,
опреде-ляется углом
расчет магнитного поля вне проводов
можно вести при допущении, что токи
проходят в бесконечно тонких нитях,
совпа-дающих с геометрическими осями
проводов. Поместим начало координат в
точку О, лежащую в середине линии,
соединяющей оси проводов (рис.19).
Скалярный магнитный потенциал в точке
М, обусловленный током в левом проводе,
опреде-ляется углом
![]() ,
отсчитываемым от направления оси x
против часовой стрелки; потенциал же,
обусловленный током в правом проводе,
опреде-ляется углом
,
отсчитываемым от направления оси x
против часовой стрелки; потенциал же,
обусловленный током в правом проводе,
опреде-ляется углом
![]() ,
отсчитываемым от направлении
,
отсчитываемым от направлении
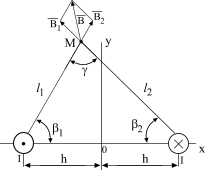

Рис. 19
оси x по часовой стрелке. Различие в направлениях отсчета объясняется тем, что токи в проводах текут в противоположных друг другу направлениях. Полная величина скалярного магнитного потенциала в точке М
![]()
Учитывая, что
![]() ,
где
,
где
![]() - плоский угол, под которым на чертеже
видны следы осей проводов из точки М,
получим:
- плоский угол, под которым на чертеже
видны следы осей проводов из точки М,
получим:
![]() .
.
Пусть
![]() во всех точках оси x,
лежащих вне линии, то есть имеющих
абсциссы
во всех точках оси x,
лежащих вне линии, то есть имеющих
абсциссы
![]() и
и
![]() .
Для этих точек
.
Для этих точек
![]() ,
поэтому
,
поэтому
![]() и магнитный потенциал будет
и магнитный потенциал будет
![]() .
.
Для определения
угла
![]() используем исходные данные задачи. Из
теоремы косинусов следует, что
используем исходные данные задачи. Из
теоремы косинусов следует, что
![]() .
.
Отсюда находим
![]() и
и
![]() .
.
Вектор магнитной
индукции в точке М имеет составляющие,
обусловленные током в левом проводнике
![]() ,
и током в правом проводнике
,
и током в правом проводнике
![]() .
Результирующий вектор магнит-ной
индукции определится как сумма его
составляющих
.
Результирующий вектор магнит-ной
индукции определится как сумма его
составляющих
![]() .
Для нахождения
.
Для нахождения
![]() предварительно вычислим углы
предварительно вычислим углы
![]() и
и
![]() .
Из теоремы косинусов
.
Из теоремы косинусов
![]() или
или
![]() ,
тогда угол
,
тогда угол
![]() .
Составляющие индукции магнитного поля
определяются путем подстановки исходных
данных задачи:
.
Составляющие индукции магнитного поля
определяются путем подстановки исходных
данных задачи:
![]() ;
;
![]() .
.
Результирующий
вектор индукции магнитного поля
![]() ,
модуль вектора индукции
,
модуль вектора индукции
![]() .
.
Векторный магнитный
потенциал
![]() в точке М находится также по принципу
наложения. Он направлен по оси z,
параллельно осям проводов:
в точке М находится также по принципу
наложения. Он направлен по оси z,
параллельно осям проводов:
![]() .
.
Предполагается,
что в начале координат векторный
потенциал
![]() .
По условию данной задачи
.
По условию данной задачи
![]() .
.
Расчет электрического поля в диэлектрике
методом интегральных уравнений.
Пример 4. В диэлектрике
с известной относительной диэлектрической
проницаемостью среды
![]() в плоскости рисунка (рис. 20) находятся
два одинаковых цилиндрических электрода.
Длина электродов
в плоскости рисунка (рис. 20) находятся
два одинаковых цилиндрических электрода.
Длина электродов
![]() ,
расстояние
,
расстояние
![]() ,
радиус сечения
,
радиус сечения
![]() заданы, при этом
заданы, при этом
![]() ,
,
![]() .
Электрод А имеет потенциал
.
Электрод А имеет потенциал
![]() ,
электрод В – потенциал
,
электрод В – потенциал
![]() .
.
Требуется:
1) составить интегральное уравнение,
которому подчиняется линейная плотность
заряда
![]() на электроде А и аналогичное уравнение
для электрода В; 2) для приближен-ного
решения интегральных уравнений по п.
1 разделить каждый электрод на три
участка одинаковой длины с неизвестными
на электроде А и аналогичное уравнение
для электрода В; 2) для приближен-ного
решения интегральных уравнений по п.
1 разделить каждый электрод на три
участка одинаковой длины с неизвестными
![]() .
Составить систему алгебраических
уравнений для определения всех
.
Составить систему алгебраических
уравнений для определения всех
![]() .
Определить коэффициенты этой системы
и, решив ее, найти закон распределения
линейной плотности заряда вдоль оси
электрода А. Вычислить емкость между
электродами.
.
Определить коэффициенты этой системы
и, решив ее, найти закон распределения
линейной плотности заряда вдоль оси
электрода А. Вычислить емкость между
электродами.
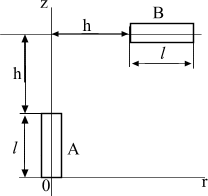
Рис. 20
Решение.
Поле заряженных
электродов в плоскости рис. 20 зависит
от координат z
и r
цилиндрической системы координат.
Потенциал
![]() произвольной точки наблю-дения Н, лежащей
в плоскости z0r,
равен
произвольной точки наблю-дения Н, лежащей
в плоскости z0r,
равен
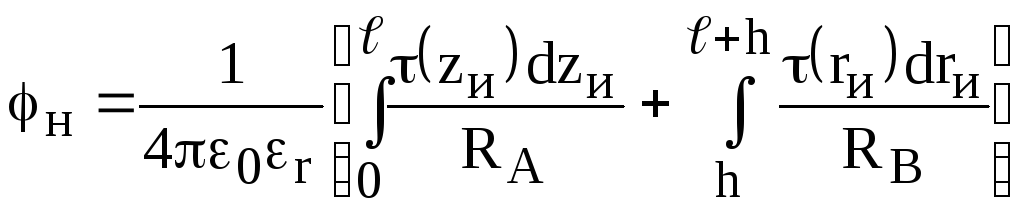
где
![]() ,
,
![]() ;
;
![]() - линейная плот-ность заряда в точке
истока;
- линейная плот-ность заряда в точке
истока;
![]() - координаты точки истока;
- координаты точки истока;
![]() - коорди-наты точки наблюдения.
- коорди-наты точки наблюдения.
Помещая точку
наблюдения на поверхность электрода А
и учитывая, что при этом
![]() ,
получим уравнение относительно
,
получим уравнение относительно
![]()
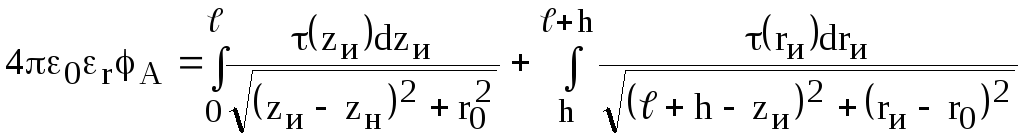 .
.![]()
Так как неизвестная
![]() находится под знаком интеграла, то
данное уравнение является интегральным
(интегральное уравнение Фредгольма
первого рода). Аналогичное уравнение
можно получить, если поместить точку
наблюдения на поверхность электрода В
и учесть, что
находится под знаком интеграла, то
данное уравнение является интегральным
(интегральное уравнение Фредгольма
первого рода). Аналогичное уравнение
можно получить, если поместить точку
наблюдения на поверхность электрода В
и учесть, что
![]()
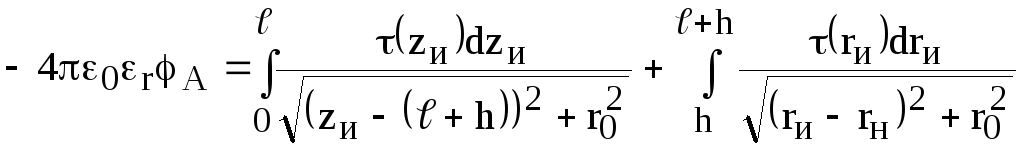 .
.
Для решения
уравнения разбиваем каждый электрод
на три равные части. Полагаем, что
линейная плотность заряда на каждом
участке
![]() неизменна и для участков электрода А
равна
неизменна и для участков электрода А
равна
![]() ,
,
![]() ,
,
![]() ,
а для участков электрода В равна
,
а для участков электрода В равна
![]() ,
,![]() ,
,![]() .
В дальнейшем будем учитывать, что
.
В дальнейшем будем учитывать, что
![]() ,
,
![]() ,
,
![]() .
Помещая точку наблюдения поочередно
на поверхность каждого участка в его
середину и вынося из под каждого интеграла
неизменные
.
Помещая точку наблюдения поочередно
на поверхность каждого участка в его
середину и вынося из под каждого интеграла
неизменные
![]() ,
получим шесть алгебраических уравнений
с шестью неизвестными плотностями
зарядов
,
получим шесть алгебраических уравнений
с шестью неизвестными плотностями
зарядов
![]() .
Делая переход к матричной форме записи,
будем иметь систему двух матричных
уравнений, соответствующих уравнениям:
.
Делая переход к матричной форме записи,
будем иметь систему двух матричных
уравнений, соответствующих уравнениям:
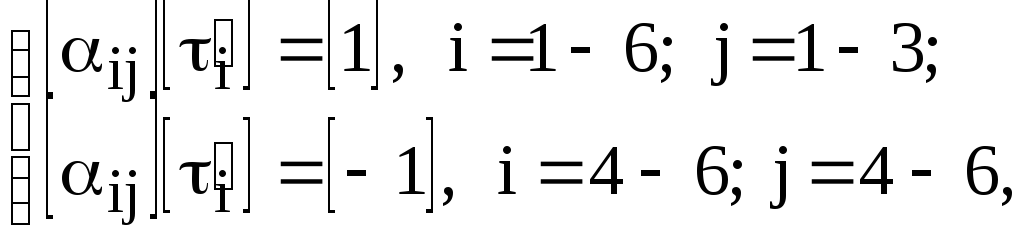
где
![]() - номер истока(участка) с линейной
плотностью
- номер истока(участка) с линейной
плотностью
![]() ;
;
![]() - номер точки наблюдения;
- номер точки наблюдения;
![]() - линейная плотность заряда в относи-тельных
единицах. Элементы матрицы
- линейная плотность заряда в относи-тельных
единицах. Элементы матрицы
![]() ,
играющие роль потенциальных коэффициентов,
рассчитываем по следующим формулам:
,
играющие роль потенциальных коэффициентов,
рассчитываем по следующим формулам:
а) при
![]()
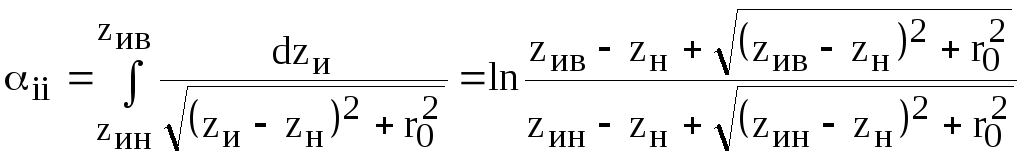 ;
;
б) при
![]()
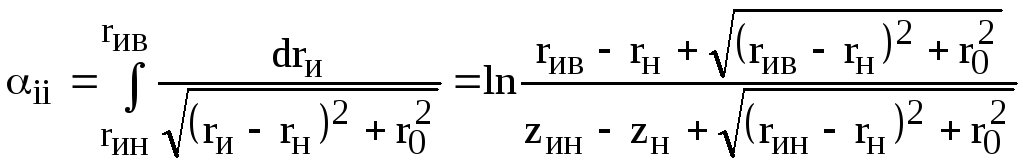 ;
;
в) при
![]()
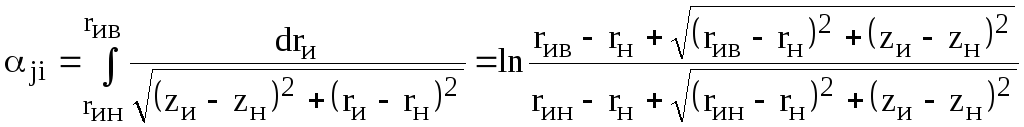 ,
,
где
![]() ;
;
г) при
![]()
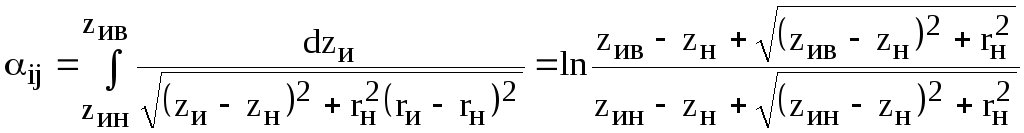 ,
,
где
![]() - соответственно верхние и нижние пределы
изменения координаты точки истока.
Следует учесть, что собственные
потенциальные коэффициенты
- соответственно верхние и нижние пределы
изменения координаты точки истока.
Следует учесть, что собственные
потенциальные коэффициенты
![]() ,
а взаимные потенциальные коэффициенты
в общем случае невзаимны, то есть
,
а взаимные потенциальные коэффициенты
в общем случае невзаимны, то есть
![]() .
.
Так как![]() ,
,
![]() ,
,![]() ,
то для определения закона распределения
заряда вдоль оси каждого электрода
достаточно решить одно матричное
уравнение в системе уравнений, например
– первое, и учесть, что
,
то для определения закона распределения
заряда вдоль оси каждого электрода
достаточно решить одно матричное
уравнение в системе уравнений, например
– первое, и учесть, что
![]() .
.
Емкость между электродами
![]() ,
,
где Q
– полный заряд электрода;
![]() число участков.
число участков.
Потенциал точки
наблюдения Н, имеющей координаты
![]() ,
определяется из выражения
,
определяется из выражения
![]() ,
,
где потенциальные
коэффициенты
![]() рассчитываются по формуле
рассчитываются по формуле
![]() .
.
Расчет электрического поля в проводящей среде
методом интегральных уравнений.
Рекомендуемый порядок решения задач на расчет электрического поля в проводящей среде методом интегральных уравнений.
-
В соответствии с методом изображений дополнить соответствующий рисунок, указанный в задании, зеркальным изображением трубы, указав, как должен быть направлен ток в нем.
-
Воспользовавшись расчетной схемой п.1 и полагая потенциалы всех точек поверхности одинаковыми (удельная электропроводность
 очень
велика) обозначить через
очень
велика) обозначить через
 ток, стекающий в землю с поверхности
трубы единичной длины, и составить
интегральное уравнение относительно
ток, стекающий в землю с поверхности
трубы единичной длины, и составить
интегральное уравнение относительно
 .
. -
Для приближенного решения интегрального уравнения п.2 разделить трубу и ее зеркальное изображение на три участка одинаковой длины с неизвестными
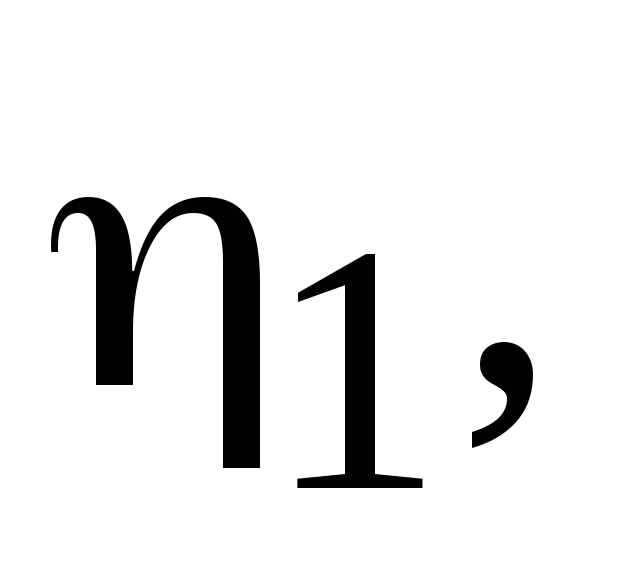
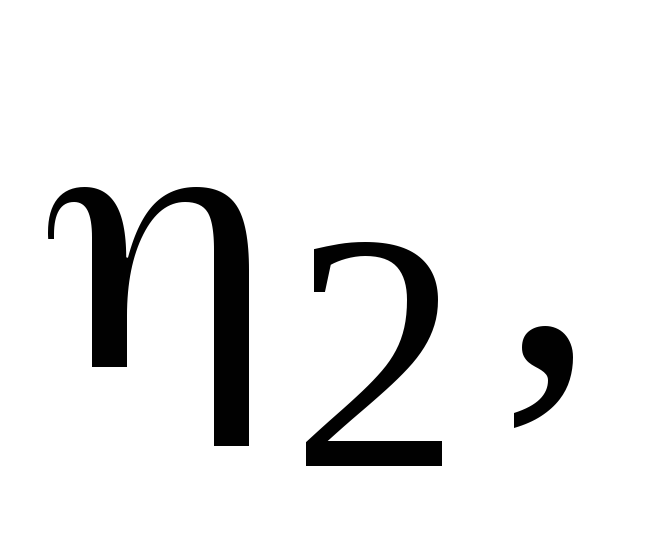
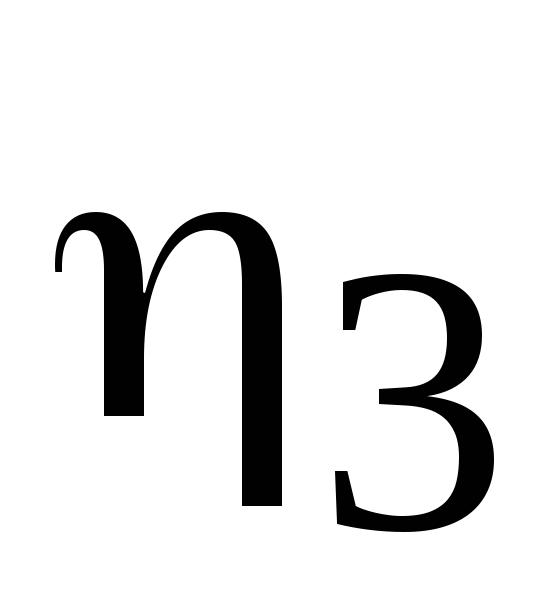 на трубе и
на трубе и


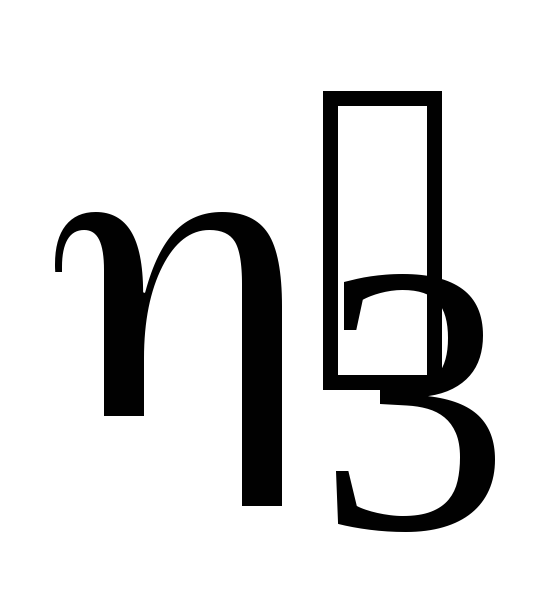 на изображении трубы; составить систему
алгебраических уравнений для определения
всех
на изображении трубы; составить систему
алгебраических уравнений для определения
всех
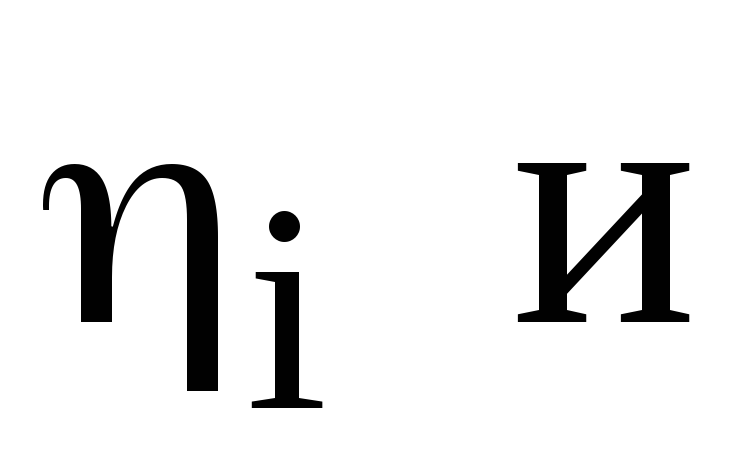
 ,
где i=1,
2, 3. Определить коэффициенты этой системы
и решить систему.
,
где i=1,
2, 3. Определить коэффициенты этой системы
и решить систему. -
Полагая потенциал бесконечно удаленной точки поля равным нулю, определить потенциал поверхности трубы (заземлителя)
 .
. -
Определить сопротивление растекания заземлителя
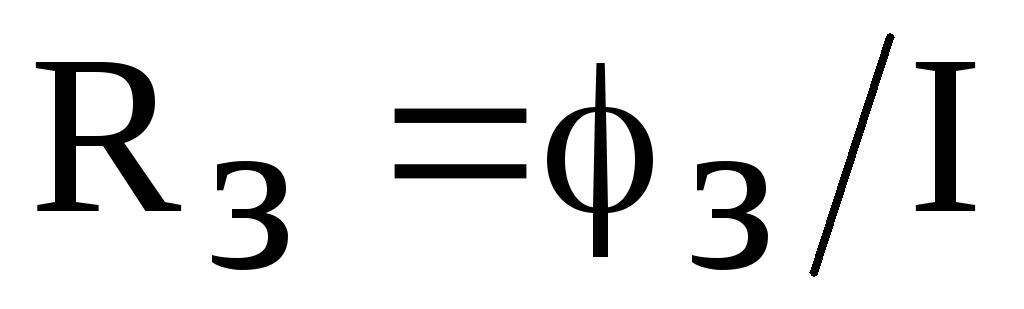 .
.
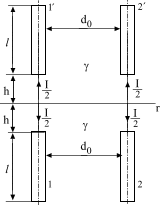
Пример 5. Заземлителем
служат две вертикально забитые в землю
стальные трубы 1 и 2 (рис. 21 а), связанные
между собой электрически. К заземлителю
изолированными проводами подведен ток
![]() А.
А.
Требуется:
1) найти распределение линейной плотности
стекающих в землю токов![]() по длине каждой трубы; 2) сопротивление
растекания заземлителя и его потенциал,
а также распределение потенциалов по
поверхности земли в плоскости чертежа,
если расстояния:
по длине каждой трубы; 2) сопротивление
растекания заземлителя и его потенциал,
а также распределение потенциалов по
поверхности земли в плоскости чертежа,
если расстояния:
![]() ,
,
![]() ,
,
![]() ,
,
![]() м.
Удельная проводимость земли
м.
Удельная проводимость земли
![]() См/м.
См/м.
Указание. Падением напряжения вдоль заземлителя пренебречь.
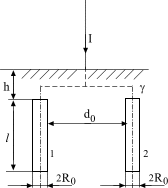
а) б)
Рис. 21
Решение.
Применяя метод
зеркальных изображений, получим расчетную
схему заземления (рис. 21 б). Поскольку
![]() ,
ток в каждой трубе можно считать
сосредоточенным на оси проводов с
неизвестной линейной плотностью
,
ток в каждой трубе можно считать
сосредоточенным на оси проводов с
неизвестной линейной плотностью
![]() ,
где
,
где
![]() -
координата точки истока И. Потенциал
-
координата точки истока И. Потенциал
![]() произвольной точки Н в плоскости чертежа
(точки наблюдения), обусловленный токами
в трубах заземлителя и его изображений,
с учетом симметрии относительно
поверхности земли равен
произвольной точки Н в плоскости чертежа
(точки наблюдения), обусловленный токами
в трубах заземлителя и его изображений,
с учетом симметрии относительно
поверхности земли равен
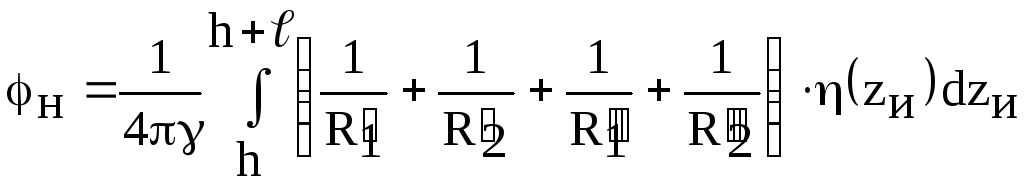 ,
,
где
![]() ,
,
![]() .
.
Если точку Н
поместить, например, на поверхность
трубы 1, то
![]()
![]() при
при
![]() и
и
![]() ;
;![]() .
.
Потенциалы всех
точек поверхности трубы 1 можно считать
одинаковыми и равными
![]() ,
так как удельная проводимость стали
значительно больше проводимости земли.
В результате, подставляя
,
так как удельная проводимость стали
значительно больше проводимости земли.
В результате, подставляя
![]() ,
получим интегральное уравнение 1 –го
рода относительно неизвестной линейной
плотности токов
,
получим интегральное уравнение 1 –го
рода относительно неизвестной линейной
плотности токов
![]() вида
вида
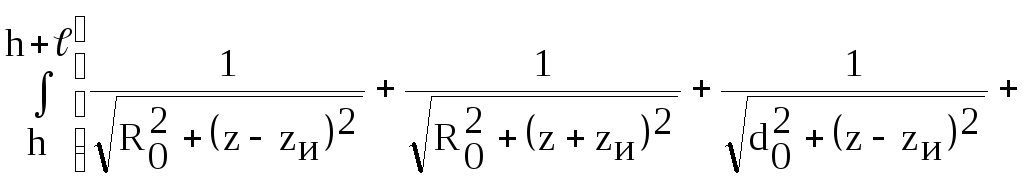
![]() .
.
Для приближенного
решения интегрального уравнения провода
1 и 2 и их изображения разобьем на n
одинаковых участков длиной
![]() со средней плот-ностью тока
со средней плот-ностью тока
![]() на каждом участке, где
на каждом участке, где
![]() (возьмем
(возьмем
![]() ).
Определим последовательно потенциал
).
Определим последовательно потенциал
![]() каждого участка трубы 1, где
каждого участка трубы 1, где
![]() ,
полагая, что точка наблюдения Н помещается
на середину поверхности участка, то
есть в точки с координатами
,
полагая, что точка наблюдения Н помещается
на середину поверхности участка, то
есть в точки с координатами
![]() ,
,
![]() .
В результате получим
.
В результате получим
![]() уравнений:
уравнений:
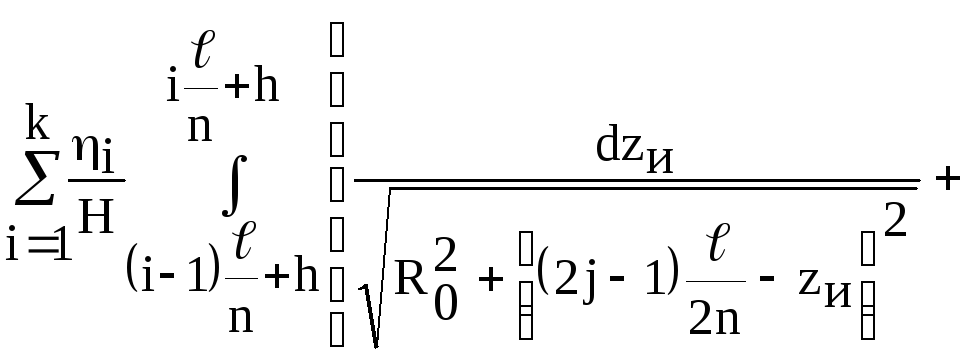
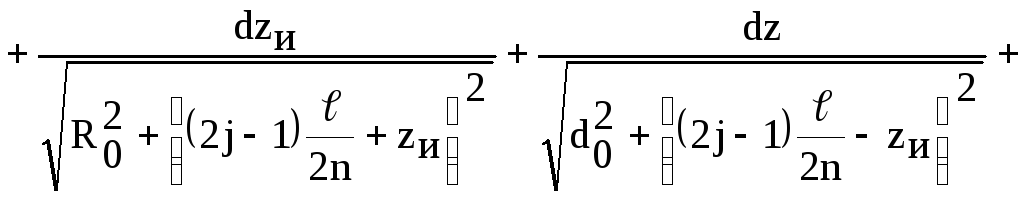

где
![]() .
.
Это система уравнений вида
![]()
где
![]() -
квадратная матрица коэффициен-тов;
-
квадратная матрица коэффициен-тов;
![]() - матрица-столбец относительных средних
линейных плотностей стекающих токов;
- матрица-столбец относительных средних
линейных плотностей стекающих токов;
![]() -
единичная матрица.
-
единичная матрица.
Каждый член матрицы
![]() ,
,![]() определяется при любых
определяется при любых
![]() выражениями,
полученными после интегрирования:
выражениями,
полученными после интегрирования:
 ;
;
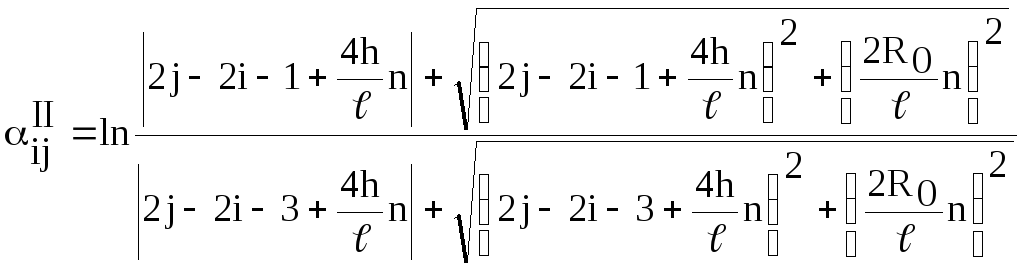 .
.
Каждый член матрицы
![]() и
и
![]() определяется соответственно выражениям
для значений
определяется соответственно выражениям
для значений
![]() и
и
![]() ,
в которые вместо радиуса
,
в которые вместо радиуса
![]() входят
входят
![]() .
.
При
![]() для заданных геометрических размеров
имеем:
для заданных геометрических размеров
имеем:
![]() ;
;
![]() ;
;
![]() ;
;
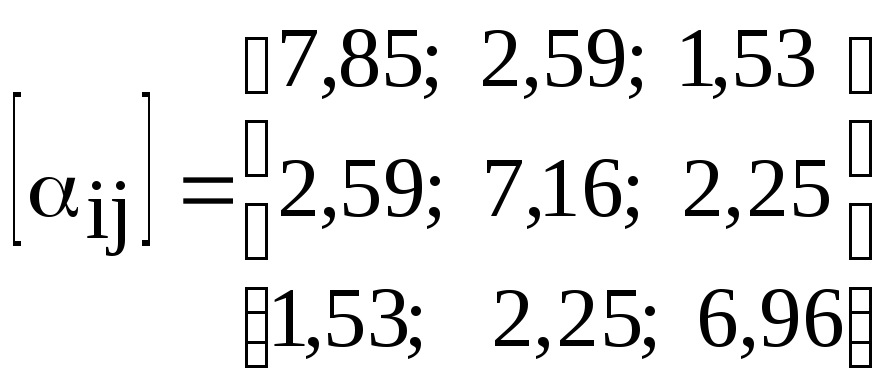
Решив систему
уравнений находим распределение
относительных линейных плотностей тока
в каждой трубе:
![]()
Ток через каждую
трубу:
![]()
Следовательно, сопротивление растекания всего заземлителя
 .
.
При
![]()
![]() и
и
![]() Ом;
Ом;
![]() 366
В.
366
В.
Распределение
потенциалов
![]() по поверхности земли (
по поверхности земли (![]() )
в силу симметрии:
)
в силу симметрии:
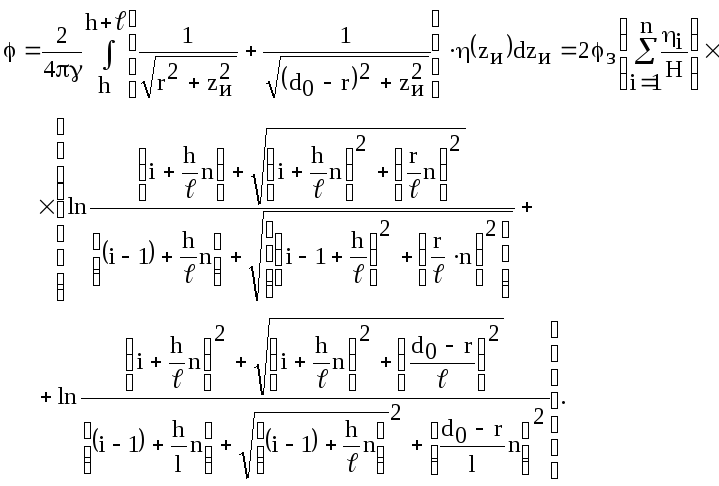
Результаты расчета представим в виде таблицы
|
|
0 |
1/6 |
2/6 |
3/6 |
4/6 |
|
|
274 |
148 |
274 |
226 |
184 |
