§ 3. Екінші ретті сызықтың центрі. Екінші ретті центрлік сызықтың теңдеуі. Анықтама. Екінші ретті сызықтың центрі деп содан жүргізілген барлық хордалар қақ бөлетін нүктені айтамыз.
Бұл
анықтама бойынша екінші ретті сызық өз
центріне симметриялы болады.
Координаталардың бас нүктесі екінші
ретті сызықтың центрінде жатса, онда
осы центрден өтетін кез-келген хорданың
екі ұшындағы
,
нүктелерінің координаталары өз ара ең
болады, яғни
және
нүктелері екінші ретті сызықтың бойында
жатқандықтан, олардың -
координаталары сызықтың теңдеуін
қанағаттандырады. Ендеше, мұндай теңдеу
екінші дәрежелі болады. Сондықтан
координаталардың бас нүктесін екінші
ретті сызықтың центріне көшірсек, онда
бұл сызықтың теңдеуінде бірінші дәрежелі
мүшелер болмау керек. Сөйтіп,
координаталардың бас нүктесі екінші
ретті сызықтың центрі болуы үшін оған
қажетті және жеткілікті тшарт: екінші
ретті сызықтың теңдеуінде (х пен у
енетін) бірінші дәрежелі мүшелер жоқ
болу керек. Алдыңғы 2-параграфта осьтердің
бағыттарын өзгертпей, координаталардың
бас нүктесін
нүктесіне көшірдік. Егер осы нүкте
екінші ретті сызықтың центрі болса,
онда (3) теңдеуде бірінші дәрежелі мүшелер
болмайды. Ендеше (3) теңдеудегі дербес
туындылар нольге тең:
.
(8)
немесе
(8)
Енді екінші ретті сызықтың біртектес емес жалпы теңдеуі берілсін:
(1)
Мұнын сол жағын 2Ғ(х,у)=2Ғ деп белгілеп, оның дербес туындыларын жазайық:
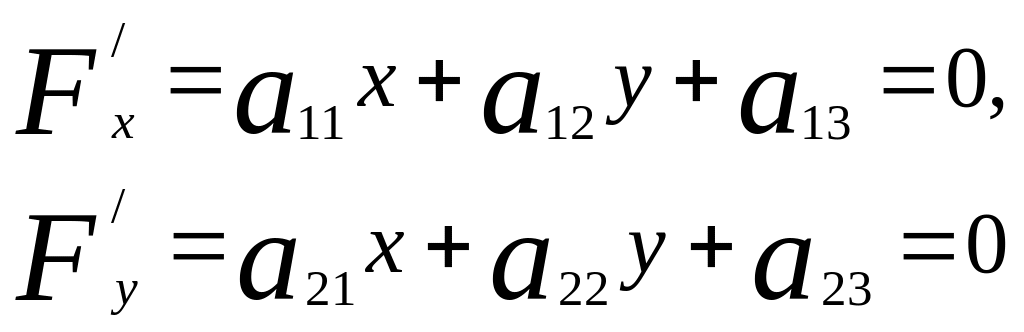(а)
2-параграфтағы (2) теңдеуді қысқаша мынадай түрде жазайық:
(3)
Мұнын дербес туындылары:
(в)
(а)
–теңдіктердегі Х,У –кез келген нүктенің
координаталары, ал (в) –теңдіктердегі
-
жаңа системаның бас нүктесінің (ескіге
қарағандағы) координаталары. Сонымен,
координаталардың бас нүктесі екінші
ретті сызықтың центрі болса, онда жоғарғы
айтуымыз бойынша дербес туындылар
нольге тең:
(
)
немесе
(
)
Ал нүктесі – екінші ретті сызықтың центрі. Ендеше (3) теңдеудің бірінші дәрежелі мүшелері болмауға тиіс, яғни (8) шарт орындалады. Сондықтан (3) теңдеуі мынадай түрге келеді:
(9)
Бұл теңдеу екінші ретті центрлік сызықтың теңдеуі деп аталады. Оның центрінің координаталарын табу үшін ( ) теңдеулері системасын шешу керек.
( ) теңдеулерінің әрқайсысы бір түзуді кескіндейді, ендеше екі түзудің қиылысқан нүктесі екінші ретті сызықтың центрі болады. Бұл теңдеулер системасын шешкенде үш түрлі жағдайдың кездесуі мүмкін.
1-жағдай. Екі түзу ( ) бір нүктеде қиылысса, онда
немесе
(А). Бұл жағдай
екінші ретті сызық центрлік сызық деп
аталады.
2- жағдай. Екі түзу ( ) өз ара параллель болса, онда
немесе
(В)
3-жағдай. Екі түзу ( ) беттессе, онда екі түзу бір теңдеуге айналады, яғни мына шарт орындалады:
(Г)
Осы жағдайда екінші ретті сызықтың центрі анықталмайды,яғни оның центрі осы беттескен түзулердің бойында болады. Мұндай түзу центрлер сызығы деп аталады.
Енді жоғарғы үш жағдайды былай айтуға болады.
1).
Егер
онда (
)
теңдеулерінің жалғыз шешімі болады.
Сондықтан екінші ретті сызықтың (1) бір
ғана центрі бар.
2). Егер ( ) теңдеулері бірігіп шешілмесе, онда екінші ретті сызықтың (1) центрі болмайды.
3). Егер ( ) теңдеулерінің шешімдері анықталмаса, онда екінші ретті сызықтың (1) центрлері көп болады, яғни екінші ретті сызықтың центрлері бір түзудің бойында жатады.
1-мысал.
Екінші ретті сызықтың
теңдеуі берілген. Оның центрін табайық.
Шешуі. ( ) теңдеулер системасы бойынша іздеген центрдің координаталарын табайық:
Сонда екінші ретті сызықтың центрі М(-1, -1) болады. Сонымен, екінші ретті сызық – не эллипс, не гипербола, небір нүктеден қиылысатын екі түзу.
2-мысал.
теңдеуімен берілген екінші сызықтың
шешімі бар ма
Шешуі. Алдыңғы мысал сияқты берілген теңдеуден дербес туындыларды табамыз:
Мұны қысқартқаннан кейін мынадай теңдеулер шығады:
Бұл теңдеулер х пен у-тің мәндері табылмайды, яғни екі теңдеу бірігіп шешілмейді. Сондықтан берілген екінші ретті сызықтың центрі жоқ, яғни екінші ретті сызықтың центрі шексізде болады.
3-мысал. Берілген теңдеудің дербес туындылары:
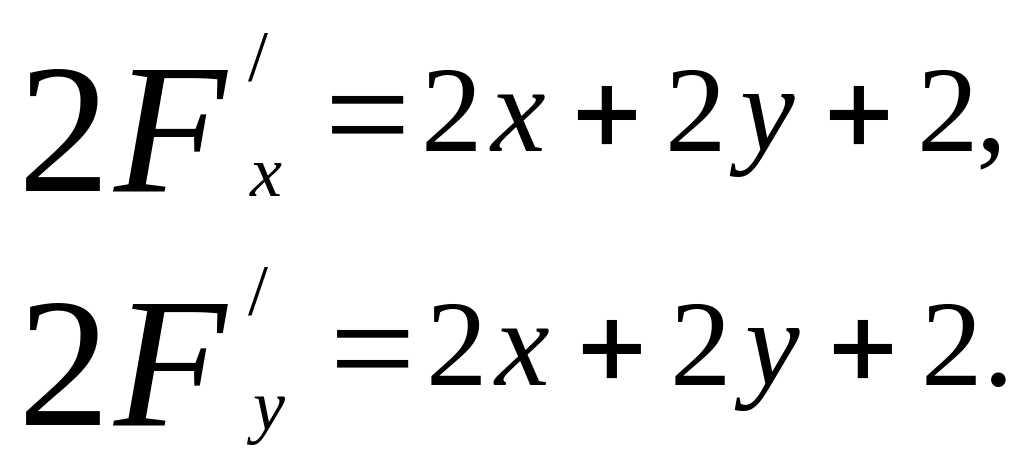
Осыдан
.
Демек, берілген қисықтың центрлері
түзуінің бойында болады, яғни екінші
ретті сызыққа центр болатын нүктелер
өте көп, олардың бәрі де осы
түзуінің бойында жатады. Мұндай түзуді
екінші ретті сызықтың центрлерінің
түзуі дейміз.