Параболаның түрін оның жабайы теңдеуі бойынша зерттеу.

П

араболаның түрін зерттеу үшін оның жабайы теңдеуін у арқылы шешейік: y =

Осыдан параболаның бойында жататын нүктелерді белгілеп, параболаның координаталар системасында қалай орналасатындығын қарастырайық.

1. Егер х-0, онда у-0. Демек, парабола координаталардың бас нүктесінен өтеді.

2. Егер х-0, онда у-+- 2рх- жорымал сан. Сондықтан ордината осініңң сол жағында параболаның нақты нүктесі болмайды.

3. Егер х –0, онда у-тің осыған сәйкес нақты мәндері болады. Х өскен сайын у-тің абсолют мәні де өсіп отырады. Х-тің әрбір мәніне у-тің әрқашанда екі мәні сәйкес келеді, яғни параболаның абсисса осіне қарағанда симметриялы екі нүктесі болады. Бұл зерттеуден мынадай қорытынды шығады: парабола- координаталардың бас нүктесінен өтіп, абсисса осіне симметриялы, шексізге дейін өсе беретін қисық сызық

Параболаға жүргізілген жанама мен нормальдің теңдеулері.

Параболаның теңдеуі және оның бойында жатқан нүкте берілсін. Осы нүктеден өтетін жанама мен нормальдің теңдеулерін табайық.

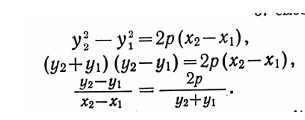
Параболаның диаметрлері. Анықтама. Берілген бағытқа параллель хордалардың ортасындағы нүктелердің геометриялық орындарын параболаның осы бағытқа түйіндес диаметрі дейміз.

Параболаның у2=2рх теңдеуі және осы параболаны қиып өтетін А1В1 хордасының у-ях+і теңдеуі берілген.

А1В1 хордасының А1 және В1 нүктелері параболаның бойында жатқандықтан, бұл екі теңдеуден осы нүктелердің координаталарын табамыз:

Осы квадрат теңдеуден Виет теоремасы бойынша:

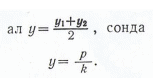
Сонымен, хорданың ортасындағы нүктесінің координаталары:

А₁В₁ хордасының ортасындағы С нүктесінің координаталары

болады. Әрбір параллель хорданың  бос мүшесі әр түрлі болғандықтан, х-тің мәні әрбір хорданың ортасындағы нүкте үшін, мысалы С₁С₂ нүктелері үшін әр түрлі болады.

Ал у=р- хорданың ортасындағы нүктенің ординатасы параболаның параметрі мен хорданың теңдеуінің бұрыштық коэффициентіне тәуелді. Ендеше бұл ордината – барлық параллель хордалардың ортасындағы нүктелер үшін тұрақты шама. Сондықтан берілген я бағытына сәйкес параболаның диаметрі мынадай болады

Бұл теңдеуден мынадай қорытындыға келеміз. Параболаның диаметрі абсцисса осіне параллель болады. Демек, параболаның барлық диаметрлері абсцисса осіне параллель болуы керек. Я коэффициентінің мәніне сәйкес абсцисса осіне параллель әр түрлі диаметрлер болуы мүмкін. Егер я-1 болса, онда диаметр у-р болады. Егер я-оо, онда диаметр у-0 болады. Соңғы жағдайда абсцисса осі параболаның диаметрі болады. Бұл параболаның бас диаметрі деп аталады (у-0) .

Эллипстің немесе гиперболаның барлық диаметрлері берілген нүктеде қиылысады. Осы диаметрлердің қиылысқан нүктесі эллипстің немесе гипболаның центрі болады. Осыған байланысты эллипс пен гиперболаны центрлік қисықтар дейміз. Ал диаметрлері өз ара параллель болғандықтан, параболаны центрсіз қисық дейміз. Басқаша айтқанда, параллель диаметрлер шексізде қиылысады, сондықтан параболаның центірі шексізде болады