Гиперболаға жүргізілген жанама және нормальдың теңдеулері

Гиперболаның теңдеуі және сол Гиперболаның бойында жатқан нүкте берілсін. Осы нүктеден өтетін жанама мен нормальдың теңдеулерін табайық

теңдеуі мен М₁(х₁, у₁) нүктесі берілген. Енді (ж) жанамасы мен (N) нормальдың теңдеулерін іздейік. Берілген М₁ нүктесінен бір көмекші қиюшы түзу жүргізіп, оның гиперболамен қиылысатын екінші нүктесін М₂(х₂, у₂) деп белгілейік. Гиперболаның бойындағы М₁ мен М₂ нүктелерінің координаталары гиперболаның қанағаттандыратын болғандықтан,

Осы екі теңдеуден қатынасын іздейміз. Ол үшін бірінші теңдеуден екіншісін аламыз, сонда

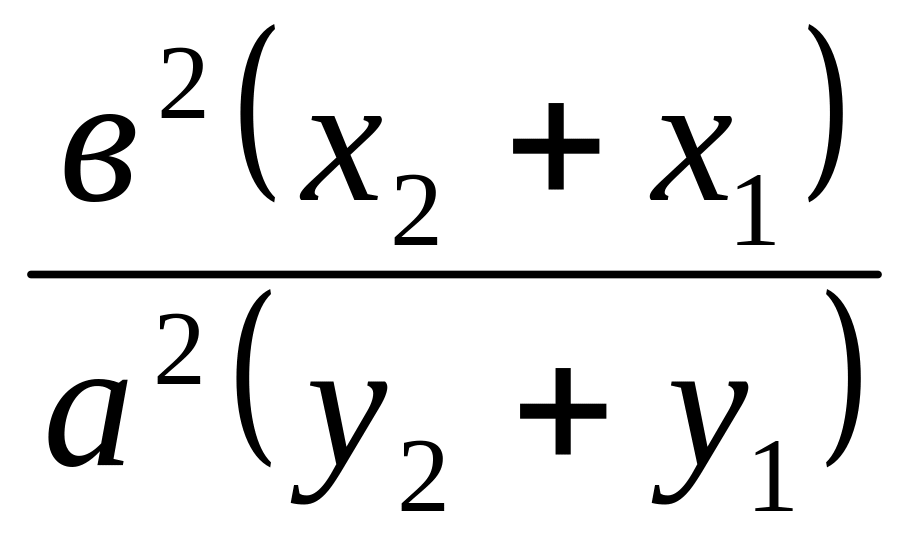= (8)

Ал қиюшы түзудің теңдеуі мынадай болады:

У – у₁= (9)

Егер М нүктесін қозғалмайтын, ал М₂ нүктесі М₁ нүктеге ұмтылады деп қарастырайық. (М₁ нүктесі М₂ нүктесінің шегі болсын) М₂ нүктесі М₁ нүктесімен шектескенде, ол қиюшы жанамаға айналады, яғни М₂ нүктесінің координаталары М₁ нүктесінің координаталарына ұмтылады: lіm x₂=x₁ lіm y₂=y₁ Сондықтан (8) теңдіктен

Lіm = (8`)

Ал (9) теңдіктен

У – у₁=lіm ( )

(8)теңдігінің мәнін (9*) теңдігіне қойып, іздеген жанаманың теңдеуін табайық:

У – у₁ = (10)

Түзулердің перпендикулярлық шарты бойынша, гиперболаға жүргізілген нормальдың теңдеуі мынадай болады

У – у₁= (11)

Енді гиперболаға жүргізілген жанама теңдеуінің қолайлы түрін шығарайық. Ол үшін (10) теңдеуіді түрлендірейік

а² уу₁– а² у₁²= б² хх₁ – б² х₁²

б² хх₁ - а² уу₁ = б² х₁² – а² у₁²

Осы теңдіктің екі жағында а² б² бөлсек

Осыдан гиперболаға жүргізілген жанаманың қолайлы теңдеуі шығады:

1 (10*)

Парабола

Анықтама. Фокус деп аталатын берілген нүктеден және директриса деп аталатын берілген түзуден ара қашықтықтары бірдей болатын нүктелердің геометриялық орындарын парабола дейміз.

Параболаның жабайы теңдеуін қорытып шығару үшін жоғарғы анықтамаға сәйкес сызба сызайық.

Берілген F нүктесінің координаталары былайша белгіленеді:

. Бұл нүкте парболаның фокусы деп аталады. Координаталардың бас нүктесінен қашықтықтағы әрі ордината

осіне параллель берілген (D) түзуін параболаның директрисасы дейміз. Параболаның бойындағы кез келген нүктені M (x, y) дейік.

Анықтама бойынша:

FM = ME

Екі нүктенің ара қашықтығының формуласы бойынша:

FM =

Осы қашықтықтардың мәндерін (1) теңдігіне қойып, параболаның жабайы теңдеуін табамыз:

мұндағы p-берілген фокус пен директрисаныңарасындағы қашықтық, параболаның параметрі; x пен y-параболаның бойындағы кез келген нүктенің ағымдық координаталары.

MF=R параболаның радиус-векторы деп аталады.

О

ның ME=FM= +x теңдігінен мынаған тең екенін көреміз:

R=

П

араболаның директрисасы 1-сызбадан анықталады:

П

араболаның эксцентриситеті: