Гиперболаның жабайы теңдеуі

Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының айырымы әрқашанда тұрақты шама болатын нүктелердің геометриялық орындарын гипербола дейміз

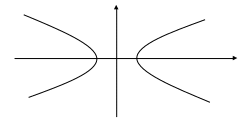
Анықтама бойынша:

2а=F₁M-F₂M

F₁F₂=2C, ОF₂=С болсын (1)

Екі нүктенің ара қашықтығының формуласы бойынша

R ₁= R₂ =

Осы R₁ мен R₂ – нің мәндерін анықтамаға қойып, алгебралық түрлендіру арқылы гиперболаның жабайы теңдеуін табайық

F₁M=R₁ F₂M= R₂

R₁ мен R₂ – нің мәндерін (1) теңдікке қойамыз

- =2a

=2a +

x + 2cx + c² + y² = 4a² + x² – 2cx + c² + y

cx – a² =a

Енді екі жағын а – ға бөлейік:

Осы теңдіктің екі жағын квадраттасақ, іздеген теңдеуді табамыз

-2cx+ a² = x² – 2cx + c² + y²

c² x² – a⁴ = a² x² + a² c² + a² y²

(c² - a²) x² - a² y² = (c² - a²) a²

Егер с² - а² = в² (2)

деп белгілесек, онда в² х² - а² у² = а² в² осыдан

(3)

Бұл теңдеу гиперболаның жабайы теңдеуі деп аталады. Мұндағы х,у - гиперболаның

Байындағы кез – келген нүктенің ағымдық координаталары а – гиперболаның нақты жарты осі, b – жорышал жарты ось.

Гиперболаның түрін оның жабайы теңдеуі бойынша зерттеу.

Гиперболаның жабайы теңдеуі у арқы өрнектейік:

Мұндағы х пен у айнымалы шамалар х – тің мәндеріне сәйкес у – тің мәндері шығады. Осы айнымалы әр түрлі мәндеріне байланысты, гиперболаның координаталар системасында қалай орналасатындығын (3`) теңдеуі арқылы қарастырайық

1. Егер х = +а болса, онда у = 0 болады. Сонда абсцисса осінің бойында гиперболаның екі нүктесі болады. А₁(-а,0) , А₂ (а,0)

2. Егер х=0 болса, онда у= ві болады. Мұнда ордината осінің бойында гиперболаның нақты нүктесі жоқ, яғни гипербола ордината осін қиып өтпейді.

3. ( ) теңдеуіне қарағанда х – тің абсолют мәні өскен сайын у- тің абсолют мәні өсіп отырады.

4. х – тің бір мәнәне у – тің әрқашанда екі мәні сәйкес келеді, яғни аргунттің бір мәніне функцияның екі мәні сәйкес келеді, демек плюс және минус таңбалары у – тің мәндері абсцисса осінің жоғарғы және төменгі жағында жатады.

5. (2) формуладан с>а. с>в. Ал

2с>2а, А₁А₂ =2а, F₁F₂ =2c В₁В₂ =2в

Осы айтылғандарға сүйене отырып, гиперболаның грфигін салуға болады. Сызбадағы А₁ және А₂ - гиперболаның төбелері А₁А₂ - гиперболаның нақты осі, В₁В₂ – жорымал осі. Координаталардың бас нүктесіне қарағанда гипербола симметриялы қисық сызық. х пен у – тің абсалют мәндері өскен сайын гиперболаның екі тармағы өсіп отырады х пен у шексіз болса онда гиперболаның нүктелеріде шексіз болады. Сызбадан ОА₁² + ОВ₁² = А₁В₁ a² + b² =с² А₁ В₁ = ОF₁ = ОF₂ =c

Егер а мен b тең болса, онда немесе x² - y² = a² болады.

Бұл тең қабырғалы гипербола деп аталады. Бұл жағдайдағы фокус координаталары мен осьтердің байланысы мынадай болады

с² - a² = b² а = b сонда с² = 2 a² с = а