Жаттығулар

1. Егер (ABCD)=-1 болса, онда 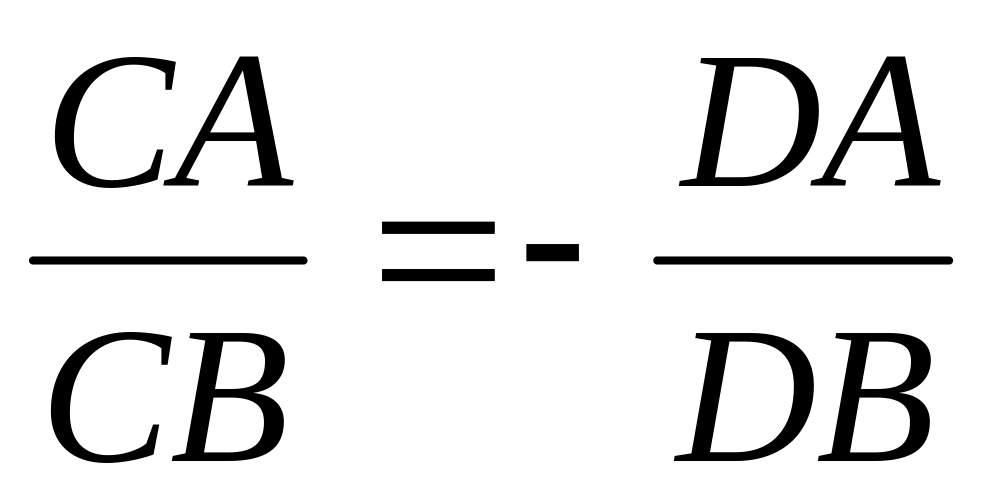орындалады. Осыны дәлелдеңдер.

2. Төрт нүктені әр түрлі алмастырғанда қос қатынастың мынадай мәндері болуы мүмкін. Осыны дәлелдеңдер.

Негізгі теоремалар. 1) Дезарт теоремасы. Егер жазықтықтағы ABC және үшбұрыштарының сәйкес төбелерін қосатын түзүлер конкуренттік болса, онда олардың қиылысатын үш нүктелеріне сәйкес қабырғалары коллинеар болады.

Теореманың шарты бойынша , және тізүлері нүктесінде O қиылсады. Ендеше, AB және түзулері бір жазықтықта жатады, олар Q нүктесінде қиылсады. Сол сияқты AC және түзулері бір R нүктесінде қиылсады, ал BC және түзулері P нүктесінде қиылсады. Бұл P,Q, Rнүктелері ABC мен ушбұрыштарының қабырғаларының әрбір созындыларында жатқандықтан, олардың бәріде әрбір созындыларында жатқандықтан, олардың бәріде әрбір үшбұрыштың жазықтығында жатады. Сондықтан P,Q, R нүктелері берілген жазықтықтарды қиылстыратын бір түзудің бойында жатады, яғни үш нүкте коллинеар болады.

2) Паскаль теореьасы. Егер алтыбүрыштың төбелері қиылсатын екі түзуді бойында кезекпе- кезек жатса, онда бұл алтыбұрыштың қарама-қарсы

жатқан қабырғаларының қиылсатын P,Q, R, нүктелері өз ара коллинеар болады.

Проекцияланғанда P және Q нүктесінің шексіздікке кететінін дәлелдеу керек.

23 пен 56 және 12 мен 45 түзулері өз ара паралель. Мұнда 16 мен 34 түзүлерінің өз ара паралель екенін дәлелдеу керек. Сызбаны пайдаланып мынаны жазайық.

Осы қатынастың біріншісін екіншісіне бөліп, мынаны табыңдар.

Сондықтан 16 түзуімен 34 түзуі өз ара параллель.

3)Брианшон теоремесы.Егер алтыбұрыштың қабырғалары кезепе-кезек Р және Q нүктелерінен өтсенда қарама-қарсы жатқан қабырғаларын қосатын үш диогоналы өз ара конкуренттік болады.

Р нүктесін проекциялағанда 14 және 36 диагональдарының қиылысқан нүктесін шексіздікке жіберейік.Ал 114 және диогональдары өз арапараллельболғандықтанына = орындалады.Мұнымен қатар , . Ендеше, . Осыдан 36 және 25 диогональдары өз ара параллель болады. Сйтіп, үш диогональдары параллель, яғни олар өз ара конкуренттік болады.

Екілік принципі. Енді жоғарғы екі теореманың формулировкаларын салыстырайық.

Паскаль теремасы. Егер алтыбұрыштың төбелері кезекпе-кезек екі түзудің бойында жатса,онда қарама-қарсы қабырғаларының қиылысатын нүктелері коллинеар блады.

Брианшон теоремалары.Егер алтыбұрыштың қабырғалары кезекпе-кезек екі нүктеден өтсе,онда қарама-қарсы жатқан төбелерін қосатын түзулер конкуренттік болады.

Осы теоремалардың формулирвкаларына қарасақ, бұлар бір-біріне ұқсайды,яғни мазмұн құрылысы өз ара бір-біріне жақын.Проективтік геометрияда мұндай теоремалар қатарласып кездесіп отырады. Осындай мазмұндары бір-біріне жақын болатын екі мәселені екілік ұғымы немесе екілік принципі деп атаған.Жазықтықтағы нүкте мен түзуде өз ара екілік принципінің элементтері болады.Паскаль мен Брианшон теоремалары өз ара екілік ұғымына жатады.

Дезарг теоремасы мен оған кері теорема екілік принципін көрсетеді.Екілік принципінің ішкі қасиеттері проективтік геометрияда толық қарастырылады.Егер екі сөйлемдегі «нүктең және «түзуң деген терминдерді бір-біріне алмастыруға блса, нда мұндай сәйкестік коррелятивтік деп атайды.

Дезарг теоремалары .Егер екі үшбұрыштың сәйкес төбелерін қосатын үш түзу бір нүктеде кездессе,онда сәйкес қабырғаларын қиып өтетін үш бір түзудің бойында жатады.

Дезаргтің кері теоремасы осыған коррелятивтік болады.Егер үшбұрыштың сәйкес қабырғалары қиып өтетін үш нүкте бір түзудің бйында жатса, онда үшбұрыштың сәйкес төбелерін қосатын үш түзу бір нүктеден өтеді.Мінеки,осы коррелятивтік екі теорема екілік принципі тіпті кездеспейді.

Параллельдік және шексіздік.Түзудің бойындағы меншікті емес нүктені шексіз алыстағы нүкте дейміз.Егер екі түзу параллель болмаса,онда олар бір меншікті

Нүктеде қиылысады.Егер екі түзу параллель болса, онда олар меншікті емес нүктеде қиылысады,яғни екі параллель түзу шексіз алыстағы нүктеде кездеседі.Мұнда мынаны естен шығармау керек,егер нүкте шексіз алыста болса,онда ол нүктеден өтетін түзулердің бәрі де өз ара параллель болады.Бұл жағдайда центірлік проеция мен параллельдік прекцияның ешбір айырыиы жоқ.Өйткені шексіз алыстағы нүктеден проекциялаған түзулердің бәрі де параллель болады.

Түзудің бойындағы (немесе жазықтықтағы ) меншікті емес нүктені «идеальдықң нүкте дейміз.Басқаша айтқанда, «идеальдықң нүкте деп түзудің бойындағы шексіз алыстағы нүктені айтамыз.

Енді кейбір мәселелерды қарастырғанда параллельдік пен шексіздік туралы ұғымның өз ара байланысына тқталайық.

1. (АВСD) = қос қатынас алайық.Берілген түзуінің бойындағы шексіз алыстағы нүкте деп белгілесек, нда қос қатынас мынадай (ABC ) символымен жазылады.Бұл (ABC ) қос қатынасын (ABCD) -нің шегі деп қарастырамыз.Мұнда А, В,С нүктелері өздерінің орындарында қалады, ал D нүктесі шексіз алыстағанда қатынасы 1-ге ұмтылады.

Бұдан мына (ABC )= анықтама шығады.Дербес жағдайы: егер (ABC )=1блса, нда С нүктесі АВкесіндісінің ртасында жатады.А, В, С, Dнүктелерінің ангармоникалық қаеынастары -1-ге тең болса,нда бұл нүктелер гармникалық нүктелердеп аталады.Бұл анықтамадан немесе .

Осы жағдайда C және D нүктелері A және B нүктелерімен гармоникалық түйіндес нүктелер деп аталады. (немесе A және B нүктелерімен C және D нүктелері бірін- бірі гармоникалық қатынасқа бөледі дейміз). Егер C нүктесі AB кесіндісінің ортасында болса, онда мына жай қатынас орындалады.

Ендеше жоғарғы (A) теңдіктен , яғни D - шексіз алыстағы нүкте. Басқаша айтқанда, егер D шексіз алыстағы нүкте болса, онда теңдігі рындалады. Сондықтан (A) қатынасынан: яғни C нүктесі AB кесіндісінің ортасында болады. Мұнда C нүктесі шексіз алыстағы нүктемен гармоникалық түйіндес нүкте деп аталады.

2. Дезарт теоремасы бойынша , , түзулурі меншікті емес О нүктесінде қиылсқан. Енді сол Декарттың теоремасына сәйкес , , түзулері шексіз алыстағы нүктеде қиылсады, яғни бол түзулер өз ара паралель болады да. О нүктесі шексіз алысқа кетеді. Мұнда паралелдік проекцияның центірі шексіз алыста болады.

Қос қатынас және проективтік координаталар. Бір L түзуінің бойындағы аффиндік координаталар системасын алайық: Осы системадағы нүктелердін координаталары болсын. Осы координаталар арқылы қос қатынасты жазайық.

Енді осыдан біртектес координаталарға көшу үшін a координатасын деп белгілейік. Осыған сәйкес жоғарғы нүктелердің координаталары былай белгіленеді:

, , , .

Бұл координаталар арқылы қос қатынас былай өрнектеледі:

.

.

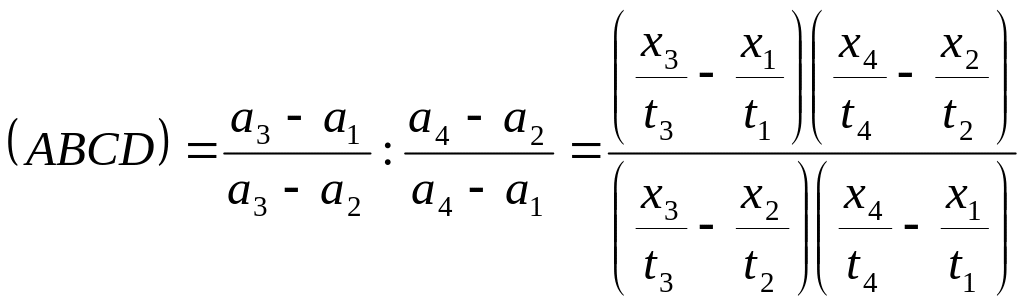A, B, C, D нүктелері проективтік түзудің бойында жатса, онда проективтік координаталар арқылы қос қатынас теңдікпен анықталады. Егенр A, B, C нүктелері меншікті болып, D нүктесі меншікті болмаса, онда теңдіктегі координаталардың дербес жағдайын алуға болады.

, , , , , , .

Координаталардың бұл мәндерін теңдікке қояйық.

.