12. Түзу мен жазықтықтың қиылысуы.

Түзу мен жазықтықтың теңдеулері берілсін:

.

Осы түзу мен жазықтықтың қиылысатын нүктесін табайық.

Түзу мен жазықтық бір нүктеде қиылысса, онда осы нүктенің координаталары берілген түзу мен жазықтықтың теңдеулерін қанағаттандырады. Сондықтан:

.

Осыдан үш теңдік шығады:

(27)

Бұл тің мәндерін жазықтықтың теңдеуіне қояйық:

Осыдан параметрін табайық:

(28)

1)Егер , яғни теңдеудің бөлімі нольден айрықша болса, онда түзу мен жазықтық бір нүктеден қиылысады.

2) Егер , , онда параметр нің мәні шексіз, ал түзу жазықтыққа параллель болады. Сондықтан нүктесі жзықтыққа жатпайды, оның теңдеуін қанағаттандырмайды.

3) Егер , онда t параметрдің мәні анықталмайды. Бұл жағдайда түзу жазықтықтың бетінде жатады, яғни түзудің барлық нүктесі жазықтықтың нүктесі болады.

13. Нүктеден түзуге дейінгі ара қашықтық.

Кеңістікте нүктесі және түзудің

теңдеуі берілген. Осы берілген нүктеден берілген түзуге дейінгі қашықтықты іздейік.

Берілген нүктеден берілген түзуге дейінгі қашықтықтың формуласын қорытып шығару үшін вектор әдісін қолданайық. Біз мұнда екі вектордың векторлық көбейтіндісін және олардың модульдарын табу жолын пайдаланамыз.

Берілген түзу болсын. - түзудің бойындағы нүкте. түзуді бағыттайтын вектор, оның бағыты осы параметрлерімен анықталады. Вектор болсын. және векторларының векторлық көбейтіндісі:

.

Бұл векторлық көбейтіндінің модулі: . Екі вектордың модульдарын былай белгілейік:

.

Енді берілген М нүктесінен берілген (а) түзуіне дейінгі қашықтық былайша жазылады:

(158-сызбаға қараңыз). Сондықтан жоғарғы теңдік былай жазылады:

.

Осыдан

.

Ал екі вектордың векторлық көбейтіндісі бойынша

.

Бұл векторлық көбейтінді мен векторының модульдары:

.

Осы мәндерді (29) теңдікке қойып, берілген нүктеден берілген түзуге дейінгі қашықтықты табайық:

немесе

(30)

Бұл теңдеуден түбірінің алымы мына үшінші ретті

Анықтауыштың минорларынан құрылған, бөлімі R₁ векторының модулі болады.

2. Лекция.

Таќырыбы: ІІ-ретті беттер. Эллипсоид және параболоидтар.Екінші ретті конус. Параболоидтар. Екінші ретті цилиндр.

Дөңгелек цилиндрдің бағыттаушысы- хОу жазықтығындағы радиусы R-ге тең шеңбер, ал жасаушылары апликата осіне параллель (163-сызба) болады. Осы сияқты хОу жазықтығындағы эллипстік

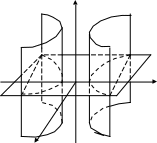
163- сызба 164-сызба

цилиндрдің бағыттаушысы – эллипс, ал жасаушылары – апликата осіне параллель түзулер. Қалған екі цилиндрлер туралы да осы сияқты айтуға болады (164, 165-сызбалар).

Цилиндрлер дегеніміз –шеңбер, эллипс, гипербола, парабола нүктелерінен

солардың жазықтықтарына перпендикуляр болып өтетін түзу сызықтардың үздіксіз қозғалысынан шығатын екінші ретті беттер. Бұл шеңбер, эллипс, гипербола және парабола цилиндрлердің бағыттаушылары деп аталады, ал цилиндрлердің беттерінде жатқан түзулер олардың жасаушылары деп аталады.

Егер эллипстік цилиндрдегі болса, онда айналмалы екінші ретті бет шығады: немесе - дөңгелек цилиндр. Сонымен дөңгелек цилиндрді эллипстік цилиндрдің дербес жағдайы деуге болады.

Сөйтіп апликата осіне параллель цилиндрлік беттің теңдеуі мынадай түрде белгіленеді:

(11)

Жоғарғы төрт теңдеуді жалпы түрде осылай жазуға болады. хОу жазықтығында (11) теңдеу қисық сызықты көрсетеді, кеңістікте осы қисық сызықтардан өтетін цилиндрлік беттерді кескіндейді.

1-мысал. Кеңістіктегі түзудің параболалық цилиндрмен қиылысатын нүктелерін табайық:

. .

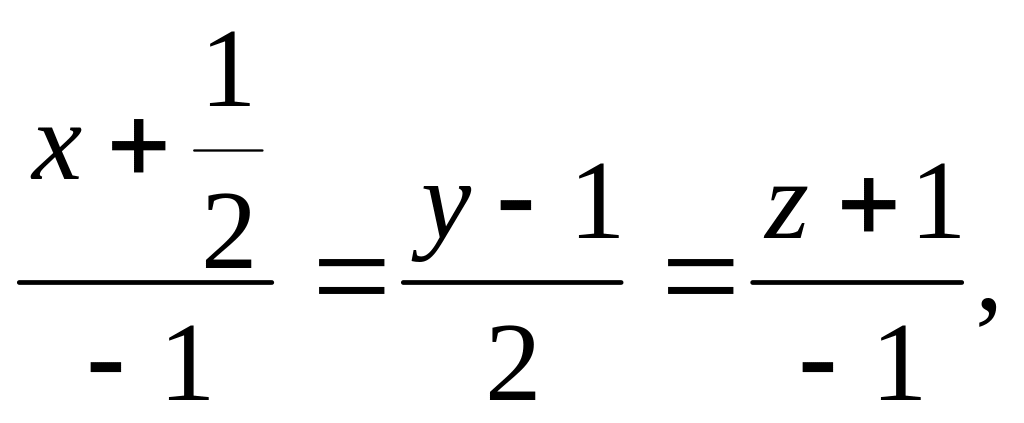Шешуі. Түзу мен параболалық

цилиндрдің қиылысатын нүкте лерін табу үшін берілген теңдеулерден x, y , z-тің мәндерін табайық (166-сызба).

-

,

, , ;

,

.

,

, .

, ,

, ;

, ,

, .

нүктесі апликата осінде (166-сызба), ал нүктесі цилиндрдің бізге көрінбейтін бетінде жатыр.

2-мысал. Мына дөңгелек цилиндр мен түзуінің қиылысқан нүктелерін табайық.

Шешуі. Алдыңғы мысалдағыдай мұнда да x, y, z-тің мәндерін табайық.

,

,

,

.

,

,

, ,

, ; , ,

, , , ;

, .

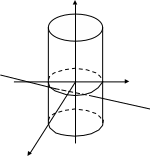
3-мысал. Мына цилиндрінің бетінде жатқанын жүргізейік.

Шешуі. нүктесінен цилиндрге жанама жүргізу үшін мына түзуі мен цилиндрдің теңдеуін біріктіріп шығарайық:

,

,

,

,

немесе

,

.

Осыдан

Егер түзу цилиндрді нүктесінен жанаса, онда жоғарғы квадрат теңдеудің түбірлері бірдей болу керек. Ол үшін болу керек. Енді жанаманың теңдеуін табайық:

, ,

, .

Енді m мен n-нің мәнін цилиндрлік жанама болу шартының теңдеуіне қояйық:

.

Конус. Екінші ретті конус деп, берілген нүктеден өтетін және бағыттаушы қисықтың бойымен жылжитын жасаушы түзудің үздіксіз қозғалғанынан шыққан геометриялық бейнені айтамыз. Конустың бағыттаушысы эллипс болсын. Конусты хОу жазықтығына параллель қиып өтетін жазықтық z=c болсын. Конустың жасаушы түзуі координаталардың бас нүктесінен өтсін, яғни конустың төбесі координаталардың бас нүктесінде жатсын. Осы конустың теңдеуін іздейік.

Координаталардың бас нүктесінен және бағыттаушы эллипстің (x, y, z) нүктесінен өтетін жасаушы түзудің теңдеуі болады, мұнда X, Y, Z – түзудің бойында жатқан кез-келген нүктенің ағымдық координаталары, ал x, y, z – эллипстің

бойындағы нүктенің координаталары. Бізге z=c түзуі берілген. Осы z-тің орнына оның мәнін қояйық:

.

Осыдан

.

Осы x пен y-тің мәндерін бағыттаушы эллипстің теңдеуіне қойып, іздеген конустың теңдеуін табайық:

, ,

. (12)

Бұл конустың перпендикулярлық қимасы эллипс. Егер a=b болса, онда конустың перпендикулярлық қимасы шеңбер болады:

. (12' )

Бұл – z осінің жанымен қозғалатын

айналмалы конус деп аталады. Егер

a=b=c болса, онда мынадай конус

шығады:

. (12" )

Сөйтіп, (12) теңдеу төбесі коор-

д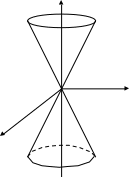 инаталардың бас нүктесінде бола-

тын апликата осіне симметриялы

түсетін екінші ретті конустық бетті

кескіндейді (168-сызба).

Қалған екі оське симметриялы

Конустық беттің теңдеулері мынадай

болады:

,

.

Бұл теңдеулердің дербес жағдайлары:

a=c,

b=c,

a=b=c, , .

Геометриялық беттердің кескіні айнымалы x, y, z мәндерінің қандай әріптермен белгіленгендігіне байланысты болмайды. Сондықтан (12" ) формуласын кіші x, y, z әріптерімен белгілеуге болады. Сонымен, конустық беттің теңдеуін зерттейік. x, y, z – айнымалы шамалар z – ке әртүрлі мән беріп, бұл теңдеудің осы z – тің мәндеріне сәйкес геометриялық мағынасын қарастырайық.

1. , . Бұл теңдеу х пен у ноль болғанда қанағаттанады. Сондықтан z ноль болғанда х пен у-те ноль болады, яғни конустық беттің төбесі координаталардың бас нүктесінде жатады.

2. , . Конустық бетті жазықтығы қиып өткенде оның қимасы шеңбер болады, яғни , ал жазықтығы хОу жазықтығына параллель.

Егер болса, онда

z – тің мәні өскен сайын конустың қимасындағы шеңбер өсе береді. z – ке теріс мәндерді берсек, онда конустың қималары координаталардың бас нүктесінің төменгі жағында болады (169-сызба).

3. Егер конустың

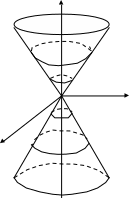теңдеуінде болса, онда

, ,

осыдан ,

немесе , . Бұл

жағдайда конустық бет

жазықтығымен мына екі ,

түзуінің бойымен қиылысады.

4. Егер болса, онда

, ,

немесе , . Мұнда

жазықтығы конусты екі ,

түзуінің бойымен қияды.

Бұл жағдайдағы конустың жасаушы

теңдеуі мынадай:

.

169-сызба Конустық беттің

теңдеуін зерттесек, онда да жоғарғыдай қорытынды болады. Мұндағы

айырма конустық беттің перпендикулярлық қимасындағы бағыттаушы қисық – эллипс. Сонымен, екінші ретті конустық бет тік бұрышты координаталар системасында мынадай теңдеулермен анықталады:

,

, (13)

.

1-есеп. теңдеуі берілген. конустың бойындағы берілген нүкте болсын. Осы нүктеден конусқа жүргізілген жанаманың теңдеуін табайық.

Шешуі.

,

,

,

,

.

Бұл t параметрінің мәніне байланысты квадрат теңдеу болады. Осы квадрат теңдеудің түбірлері бірдей болу үшін мынадай шарт орындалады:

Сондықтан осы теңдеу мен мына

теңдеуінен параметрлерін шығарсақ, онда конусқа жүргізілген жанама түзудің теңдеуін табамыз:

(14)

2-есеп. Төбесі координаталардың

,

,

анықталатын конустың теңдеуін табайық.

Шешуі. Конустың жасаушы теңдеуінен

, , .

Осы x, y, z – тің мәндерін жоғарғы теңдеуге қояйық:

,

,

.

Енді конустың теңдеуін табайық:

, ,

,

, .