9. Екі түзудің арасындағы бұрыш. Екі түзудің перпендикулярлық және параллельдік шарттары.

Екі түзу берілсін:

Осы екі түзудің арасындағы бұрышты іздейік.

Бірінші түзудің осьтерімен жасайтын бұрыштары , екінші түзудің сол осьтермен жасайтын сәйкес бұрыштары болса, онда олардың бағыттаушы косинустары мынадай болады. (7-пункттегі (15) формула):

(18)

(18’)

Екі түзудің арасындағы бұрышты φ деп белгілесек, онда екі вектордың арасындағы бұрышты анықтайтын формула бойынша (векторлық алгебра):

осыған (18) теңдеулердегі косинустардың мәндерін қояйық:

(20)

Айқасқан екі түзудің арасындағы бұрыш деп, берілген екі түзуге параллель болатын, кеңістіктің кез келген нүктесінен жүргізілген екі түзудің арасындағы бұрышты айтамыз. Бұл бұрыш бірін- бірі 180Ә- қа толықтыратын және сол 180Ә-тан әрқашанда кем болатын екі бұрыштың біреуі болады.

Егер екі түзу өзара перпендикуляр болса ( ) , онда болады. Сонда (20) теңдік былай жазылады:

Осыдан кеңістіктегі екі түзудің перпендикулярық шарты шығады:

. (21)

Егер екі түзу өзара параллель болса (φ=0), онда олардың сәйкес бағыттаушы косинустары тең болады немесе шамалары бірдей, ал таңбалары қарама-қарсы:

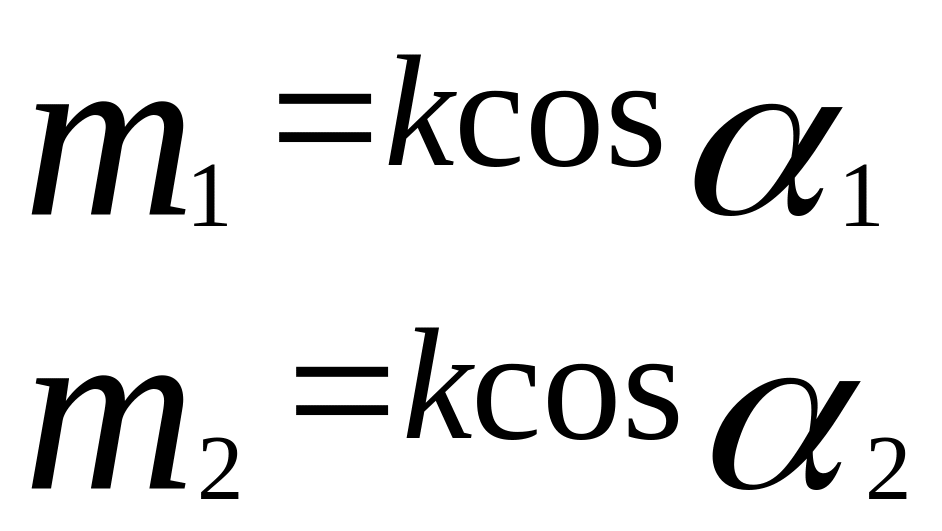
Осыдан екі түзудің параллельдік шарты шығады:

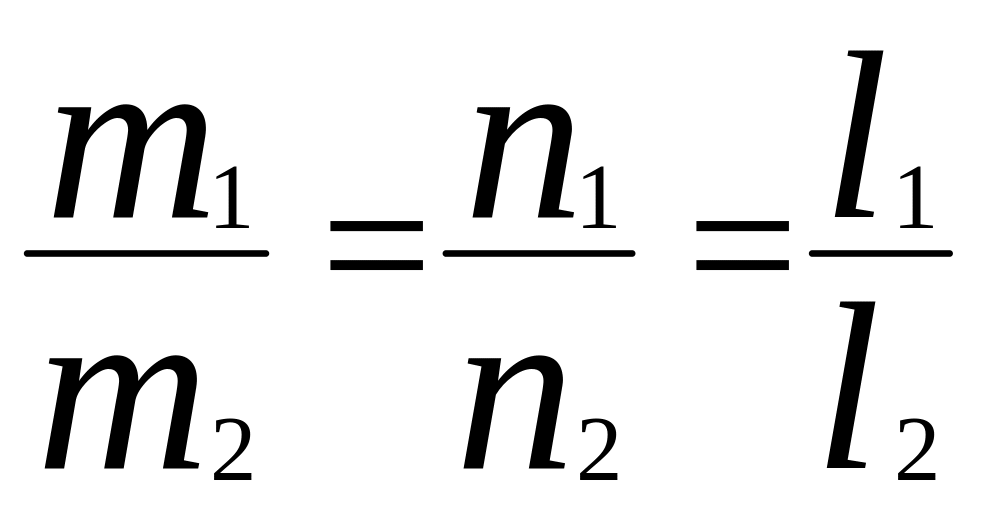(22)

10. Екі нүктеден өтетін түзудің теңдеулері (екінші әдіс).

Кеңістікте екі нүкте берілсін: .

Осы екі нүктеден өтетін түзудің теңдеулерін іздейік. Кеңістікте берілген бір нүктеден өтетін түзудің теңдеулері бізге мәлім:

(4)

Берілген түзу екінші нүктеден де өтетін болғандықтан, оның теңдеулері былайша жазылады:

.

Соңғы теңдеулердің қатынасын t деп белгілейік:

.

Осыдан m,n,l параметрлерін өрнектейік:

Осы m,n,l параметрлерінің мәндерін (4) формулаға қойып, екі нүктеден өтетін түзудің теңдеулерін табайық:

(5)

Егер нүктелері бір түзудің бойында жатса, онда (5) теңдеулерді М₃ нүктесінің координаталары қанағттандыру керек. Сондықтан үш нүктенің бір түзудің бойында жату шарты мынадай болады:

(23)

11. Түзу мен жазықтықтың арасындағы бұрыш.

(157-сызба)

Анықтама.Түзу мен жазықтықтың арсындағы бұрыш деп, оның жазықтыққа түсірілген проекциясы мен түзудің арасындағы кез келген екі сыбайлас бұрыштың біреуін айтамыз. векторларының арасындағы бұрыш анықтама бойынша болады (157-сызба).

Оның мәні: немесе Барлық жағдайда: . Сондықтан - сүйір бұрыш, ал (келтіру формуласы бойынша) .

Түзу мен жазықтықтың теңдеулері берілген:

,

Осы түзу мен жазықтықтың арасындағы бұрышты табайық.

Жазықтық пен түзудің арасындағы бұрышты деп белгілейік.

Берілген түзу мен жазықтыққа жүргізілген нормальдық вектордың арасындағы бұрыш (157-сызба) (90Ә- ) болады. n= {A, B, C}, t= {m, n, l} векторларының арасындағы бұрыштың косинусы мынадай болады:

немесе , яғни

, (24)

мұндағы .

(AD) түзуі мен Р жазықтығының бағыттаушы косинустары:

Егер =0 болса, онда болады. сондықтан (24) теңдік былай жазылады:

Осыдан түзу мен жазықтықтың параллельдік шарты шығады:

Егер болса, онда AD түзуі Р жазықтығына перпендикуляр, ал нормалына параллель болады. Сонда бұл түзу мен номальдың осьтермен жасайтын бұрыштары бірдей болады. сондықтан түзу мен жазықтықтың перпендикулярлық шарты мынадай теңдеу арқылы жазылады:

.