Жазықтықтың нормаланған теңдеуі

q – кез келген жазықтықболсын. /204-сурет/. Координаталар бас нүктесінен q жазықтығына дейінгі қашықтықты р арқылы, ал q жазықтығының нормальдық векторы мен координаталар осьтерінің арасындағы бұрыштарды арқылы белгілейік. Жазықтықтың кеңістікте орналасуы және р шамаларының берілуімен толық анықталатыны айқын. q жазықтығының теңдеуін осы шамалар арқылы өрнектейік.

М₀ – координаталар бас нүктесі арқылы q жазықтығына перпендикуляр өтетін түзудің осы жазықтықпен қиылысу нүктесі, - q жазықтығының бірлік нормальдық векторы болсын. М₀ нүктесі мен векторының координаталары берілген және р шамалары арқылы былай өрнектеледі: , . нүктесі арқылы өтетін және нормальдық векторы /А;В;С/ нүтесі арқылы болатын жазықтықтың теңдеуін алдық: . Осы теңдеуге М₀ нүктесі мен векторының координаталарын қойып, q жазықтығының теңдеуін аламыз:

,

немесе

.

- бірлік векторының координаталары болғандықтан , демек,

. (1)

(1) теңдеуі жазықтықтың нормаланған теңдеуі деп аталады. Бұл теңдеуде х,у және z айнымалыларының коэффициенттері жазықтықтың бірлік нормальдық векторының координаталары болады, ал бос мүше /-р/ «минусң таңбасымен алынған координаталар бас нүктесінен жазықтыққа дейінгі қашықтыққа тең.

/204-сурет/

Мысал, теңдеуі нормаланған жатпайды, өйткені векторы бірлік вектор емес және теңдеудегі бос мүшесі оң таңбалы. Берілген теңдеуді -ге көбейтелік. Алынған теңдеу нормаланған болады, өйткені -бірлік вектор екенін оңай тесеруге болады, ал теңдіктің бос мүшесі теріс таңбалы. Қарастырып отырған жазықтықтың нормальдық векторы координаталар осьтерімен бұрыштарын жасайды, сонда , яғни . Жазықтық координаталар бас нүктесінен 10 бірлік қашықтықта өтеді.

Жазықтықтың жалпы теңдеуін әрқашан нормаланған теңдеуге келтіруге болады. Ол үшін теңдеудің екі жағын да болғанда , ал болғанда - нормалаушы көбейткішке көбейту керек. Шынында да, егер болса, онда

теңдеуі нормаланған теңдеу болады, өйткені

векторы бірлік вектор және . Егер, болса,онда

теңдеуі нормаланған теңдеуі болады.

Есеп. Координаталар бас нүктесінен жазықтығына дейінгі қашықтықты есептеу керек.

Шешуі. болғандықтан, нормалаушы көбейткіш -ге тең. Берілген жазықтықтың нормаланған теңдеуі

болады. Жазықтықтың нормаланған теңдеуінің бос мүшесінің геометриялық мағынасын ескеріп, іздеген қашықтықтың 25-ке тең екенін аламыз.

Нүктеден жазықтыққа дейінгі қашықтық

Кез келген нүктесінен өзінің нормаланған теңдеуімен берілген q жазықтығына дейінгі қашықтықты табайық. Бұл қашықтық М₁К кесіндісінің ұзындығына тең,

К - М₁ нүктесінің q жазықтығына проекциясы /205-сурет/. М₀ - q жазықтығының координаталар бас нүктесі арқылы осы жазықтыққа жүргізіл-

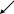
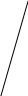
z M₁ k n d 0 M₀ k y і j x

ген перпендикулярмен қиылысу нүктесі; - q жазықтығының бірлік нормальдық векторы болсын. Іздеген қашықтық векторының мен векторы бағытына проекциясының модуліне тең. Сонымен,

векторының бағытына проекциясын осы векторлардың скалярлық көбейтіндісі арқылы өрнектейік. және болғандықтан, және , демек,

(2)

Сонымен, нүктеден жазықтыққа дейінгі қашықтық жазықтықтың нормаланған теңдеуінің координаталарын қойғаннан шыққан санның модуліне тең.

Есеп. М(0;1;1) нүктесінен жазықтығына дейінгі қашықтықты анықтау керек.

Шешуі. Жазықтықтың теңдеуін нормалдаймыз. Нормалаушы көбейткіш ге тең болғандықтан, теңдеуін аламыз. (2) формуласы бойынша қашықтықты табамыз: .