§ 6. Екінші ретті центрлік сызықтың теңдеуін зерттеу. Бұл параграфта екінші ретті центрлік сызықтың теңдеуі зерттеледі, яғни мына теңдеудің

( )

элементтерінің мәндеріне байланысты оның қандай гео-метриялық бейнені көрсететіндігін қарастырайық.

1-жағдай. мен -нің таңбалары плюс, ал мен ның таңбалары қарама-қарсы (+,-) болсын. Бұл жағдайда нақты эллипс шығады. Енді осыған сәйкес инварианттардың таңбаларының қандай екенін анықтайық. Ол үшін 5-параграфта келтірілген инварианттарды келтірейік:

Ал

мен -нің таңбалары плюс болғандықтан >0, >0, мұны мен нольге тең емес деп ұйғарамыз, яғни Сонымен қатар Бұл жағдайда қойылған шарт бойынша Сонымен, егер болса, онда нақты эллипс шығады. Бұл жағ-дайда екінші ретті центрлік сызықтың теңдеуі эллипстің жабайытеңдеуіне келтіріледі:

2-жағдай. Егер мен таңбалары минус, мен -ның таңбалары қарама-қарсы болса, онда жорымал эллипс шығады. Инварианттардың таң-балары: болады .Сонымен, бұл жағдайда болса, онда жорымал эллипстің теңдеуі шығады:

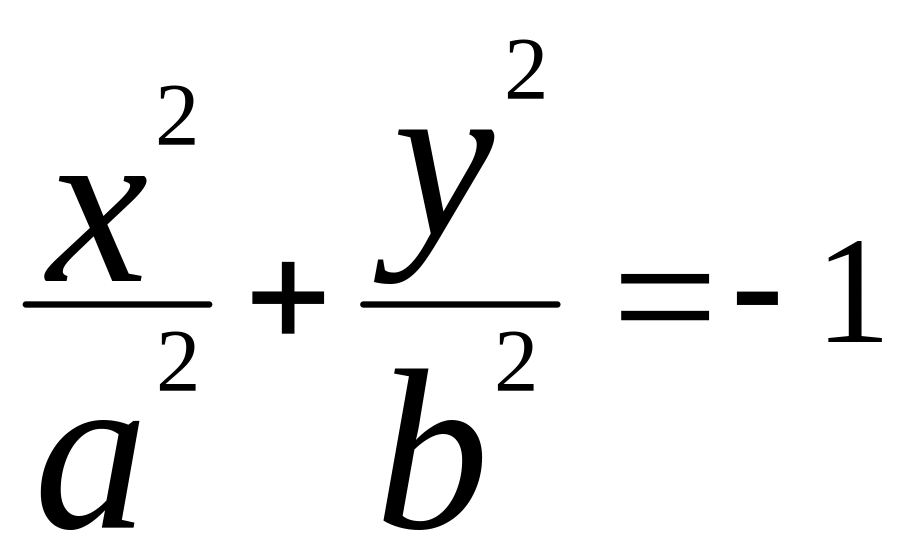
Бұл екі жағдай қысқаша былай тұжырымдалады: егер мен нің таңбалары бірдей болып, болса, онда екінші ретті центрлік сызықтың теңдеуі нақты немесе жорымал эллипстікі болады.

3-жағдай. мен нің таңбалары бірдей болып, болса, онда мынадай теңдеу шығады:

(себебі ).

Бұл теңдеу пен -тің ноль болған мәндерін қанағаттандырады. Сондықтан болғандықтан, екінші ретті сызықтың центрлік теңдеуі нүктені көрсетеді:

4-жағдай. -дің таңбасы плюс, -нің таңбасы минус болып, болса, онда ( ) теңдеуі гиперболаның теңдеуі болады.

Егер нің таңбасы плюс, -дің таңбасы минус болып, болса, онда да гипербола шығады.

Қысқаша айтқанда, мен -нің таңбалары қарама-қарсы, болса, онда теңдеу гиперболаны көрсетеді.

5-жағдай. мен -нің таңбалары әр түрлі, ал .Сонда екінші ретті центрлік сызықтың теңдеуі мынадай болады:

мен -нің таңбалары әр түрлі болғандықтан, бұл теңдеу бір нүктеден қиылысатын екі түзу көрсетед:

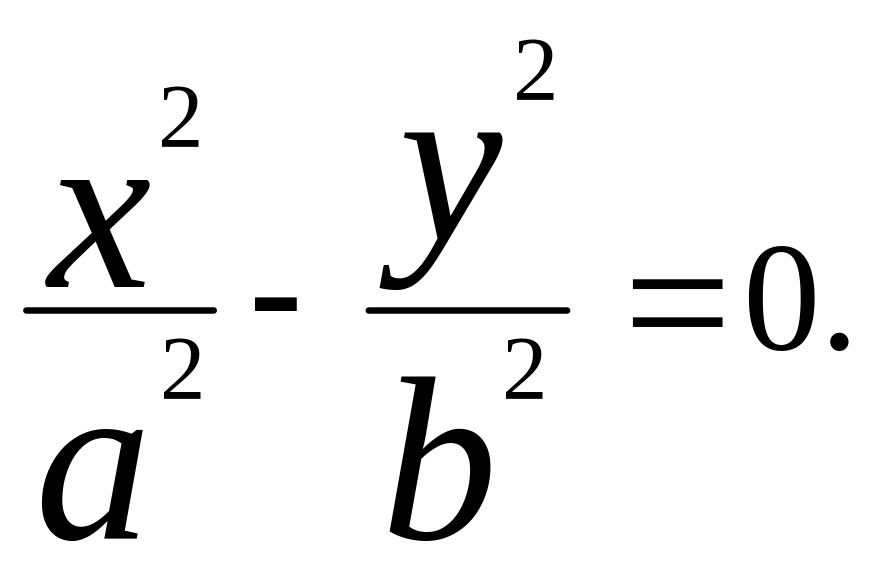
Екінші ретті центрлік сызықтың жоғарыда зерттелген бес түрлі жағдайы 3-таблицада келтіріліп отыр.

3-таблица.

№	Сызықтың қандай болу шартты.	Сызықтың аты	Характеристикалық теңдеу	Жабайы теңдеу
1		Нақты эллипс
2		Жорамал эллиас
3		Нүкте
4		Гипербола
5		Қиылысатын екі түзу

Қортынды. Екінші ретті центрлік сызықтың

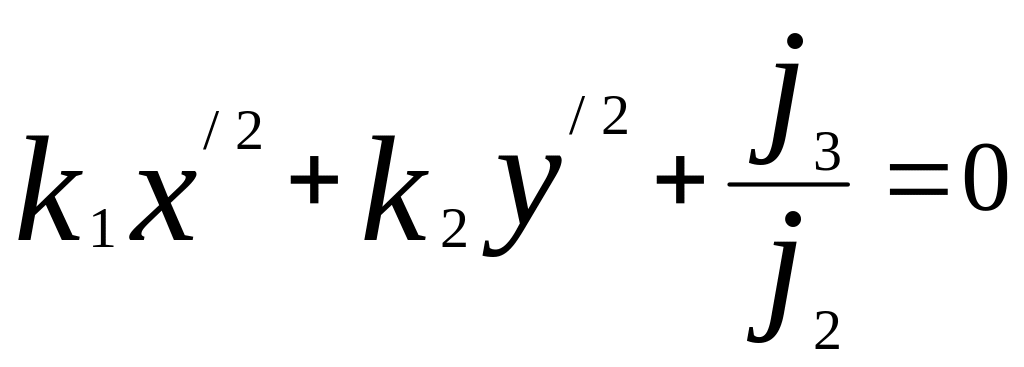( ) жабайы теңдеуін шешу үшін, ең алдымен екінші инварианттың ( ) нольден артық не кем екенін анықтау керек. Сонан кейін бірінші инвариант ( ) пен үшінші ( ) инварианттарды анықтап, сызықтың қандай екенін бі-леміз. Бұдан соң характеристикалық теңдеуінен оның түбірлерін тауып, ( ) теңдеуге осы табылған түбірлердің мәндері мен ин-варианттардың мәндерін қойсақ, екінші ретті сызықтың жабайы теңдеуі шығады.

1-мысал. Екінші ретті сызықтың теңдеуін жабайы түрге кетірейік.

Шешуі. Инварианттарды табайық:

Сонымен, Бұл екінші ретті сызық эллипс болады.

Характерисеикалық теңдеу: Оның түбірлері:

Енді эллипстің жабайы теңдеуін табайық:

2-мысал. Мына теңдеуді жабайы түрге келтірейік.

Шешуі. Инварианттар мен характеристикалық теңдеудің түбірлерін тауып, екінші ретті сызықтың теңдеуін жабайы түрге келтірейік:

Енді характеристикалық теңдеудің түбірлерін анықтар, іздеген теңдеуді жазайық:

Сонымен, екінші ретті сызық гипербола болады.

3-мысал. Мына теңдеуді жабайы түрге келтіріп, оның қандай екінші ретті сызық екенін білейік.

Шешуі. Инварианттарды тауып, характеристикалық теңдеуді құрайық. Сонан соң характеристикалық теңдеудің түбірлерін тауып, берілген теңдеуді жабайы түрге келтірейік.

Сонымен,

Инварианттардың мәндері осындай болғандықтан, берілген теңдеу қиылысатын екі түзудікі болады. Енді осы екітүзудіңтеңдеуін табацық:

Бұл теңдеудің коэффиценттерін екі әріппен белгілейік:

Сонда теңдеу мынадай түрде жазылады: Осыны жіктеп, екі түзудің теңдеуін табайық:

Бұл – жаңа координаталар системасындағы қиылысатын екі түзу. Мұндағы a,b- тұрақты сандар.

Ал ескі координаталар системасындағы қиылысатын екі түзудің теңдеуін табу үшін берілген теңдеуді квадрат теңдеудің формуласы арқылы шешейік:

Осыдан екі теңдеу шығады:

у

2y=x+7+3x+1, 4x-2y+8=0, 2x-y+4=0,

2y=x+7-3x-1, 2x+2y-6=0, x+y-3=0,

2x-y+4=0,

x+y-3=0.

Сонымен, берілген теңдеу осындай қиылысатын екі түзу болады.

Ескі координаталар системасына қарағандағы жаңа координаталар системасының центрі осы екі теңдеуден табылады:

2х-у+4=0

x+y-3=0

Осы екі теңдеуден х пен у-ті табамыз:

3x+1=0, x=- y=3+

.

Жалпы теңдеу бір нүктеде қиылысатын екі түзудікі болса, онда ол теңдеу жаңа координаталар системасында қолайлы түрге келмейді. Өйткені жаңа координаталар системасында мен көбінесе иррационал сандарболады. Сондықтан қиылысатын түзулердің теңдеулерін жалпы теңдеуді жіктеп немесе оны квадрат теңдеу ретінде шығару керек.

§ 7. Екінші ретті центрлік сызықтың бас диаметрлері. Анықтама. Параллель хордалардың дәл орталарынан өтетін диаметрді осы хордаларға түйіндес диаметр дейміз. Екінші ретті сызықтың осі деп түйіндес хордаларға перпендикуляр болатын диаметрді айтамыз. Бұл анықтама бойынша екінші ретті сызық оське симметриялы болады. Симметриялы осьтермен беттесетін диаметрлерді бас диаметрлер дейміз.

Екінші ретті центрлік сызықтар: эллипс, гипербола және шеңбер. Эллипс пен гиперболаның екі-екіден симметриялы осьтері, яғни екі-екіден бас диаметрлері бар, ал шеңбңрдің кез келген диаметрі оның рсі болады.

Екінші ретті центрлік сызықтың бас диаметрлерінің теңдеулерін қорытып шығарайық. Екінші ретті центрлік қисықтың бас диаметрлері сол екінші ретті қисықтың центрінен өтеді. Ендеше центрдің координаталарын десек, бас диаметрдің теңдеуі бір нүктеден өтетін түзудің теңдеуіндей болып жазылады:

Ескі абсцисса осін бұрышына бұрсақ, онда ескі ось пен жаңа осьтің арасындағы бұрыштың тангенсі бұрыштық коэффицент болады: Бұл k белгісіз. Бір бас диаметр осы осінің бойында жатыр, яғни бұл осьтің өзі бас диавметр. Осының бұрыштық коэффицентін іздейміз. Бұрыштық коэффицентті табу үшін бесінші параграфтағы (15) теңдіктерді пай даланайық. Қарастырып отырған жағдайда ал болсын дейік. Сонда (15) теңдіктер бойынша былайша жазылады:

немесе

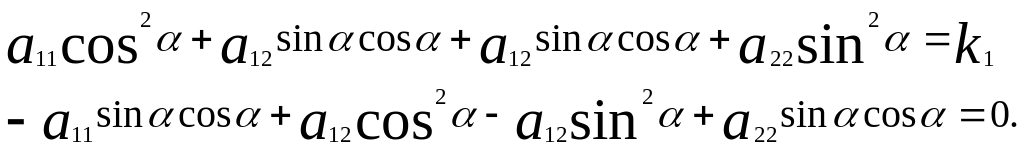
Енді бірінші теңдеуді екіншісін көбейтіп, бұл теңдіктердің екі жағын қоссақ мынау шығады:

(21)

Енді теңдеуіне k-ның мәнін қойсақ:

(22)

Бұл – бір бас диаметрдің теңдеуі. Енді екінші бас диаметрдің теңдеуін дәлелдеу үшін екі түзудің перпендикулярлық шартын пайдаланайық. Екінші бас диаметр -тің бойында жатсын. Осыған сәйкес бұрыштық коэффицентті деп белгілесек, онда екі түзудің перпендикулярлық шарты бойынша:

немесе

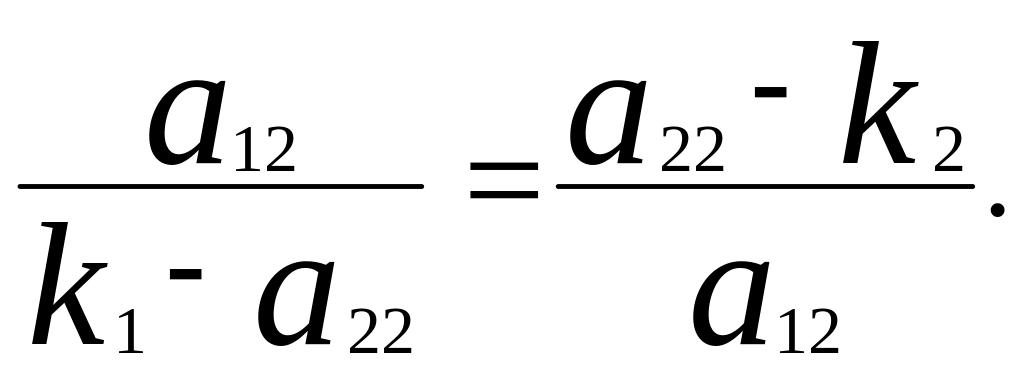
Осы теңдіктің дұрыс екендігін көрсетейік:

Сонымен, теңдеуі тепе-теңдік болады. Ендеше, екінші бас диаметрдің теңдеуі мынау:

(23)

Мысал. Мына екінші ретті сызықтың бас диаметрін табайық.

Шешуі. әуелі екінші ретті сызықтың центрін табамыз:

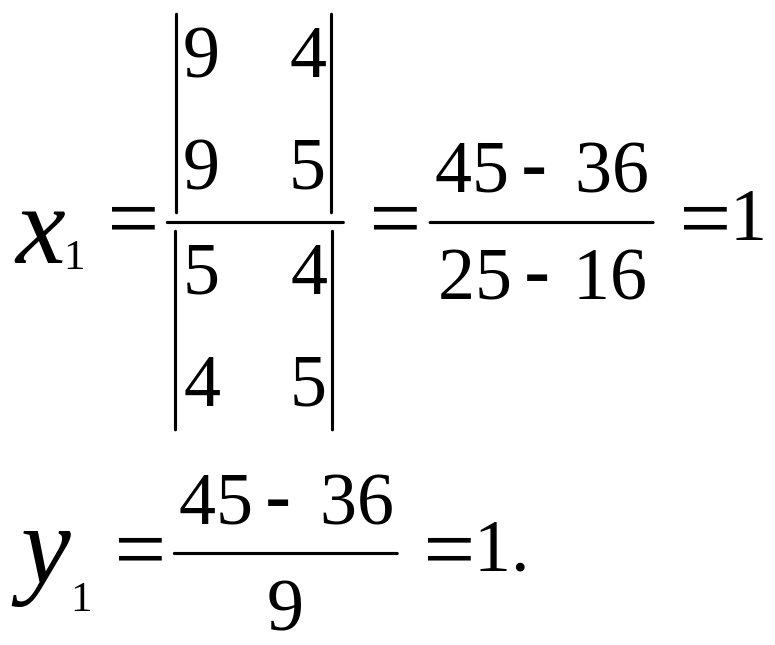Сонымен,

Бұрыштық коэффиценттерді табайық:

Енді (22), (23) формулаларға центрдің координаталары мен коэффиценттерінің мәндерін қоцып, іздеген бас диаметрлердің теңдеулер-ін табамыз:

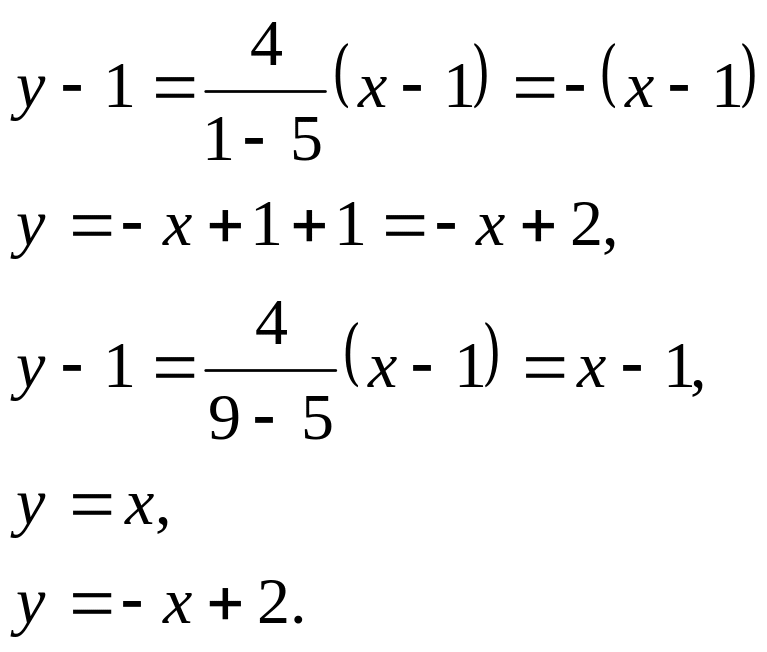
§ 8. Екінші ретті центрлік сызықтың графигін салу. Алдыңғы параграфтарда дәлелденген формулаларды қолданып, неді екінші ретті центрлік сызықтың графигі ескі координаталар системасында әр түрлі орналасуы мүмкін. Бұлардың графиктерінің ескі координаталар системасында орналасуына байланысты олардың қалай салынатынын көр-сетейік. Екінші ретті центрлік сызықтың графигін құру үшін:

1). жалпы теңдеуді жабайы түрге келтіреміз:

2) екінші ретті сызықтың центрін тауып, оның бас диаметрлерінің теңдеулерін анықтаймыз:

3) бұрыштық коэффицентті табамыз:

4) екінші ретті сызықтың табылған центрінен бас диаметрлерді жүргізіп, табылған жабайы теңдеудің мәніне қарай екінші ретті центрлік сызықтың графигін саламыз.

1-мысал. Мына екінші ретті сызықтың графигін салайық.

Шешуі. 1). Берілген теңдеуді ( ) формуласы бойынша жабайы түрге келтірейік:

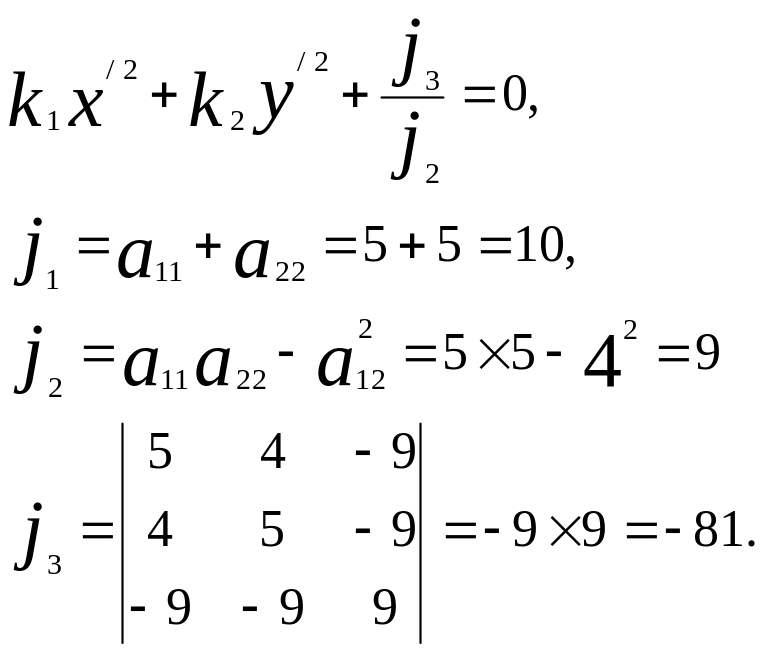
Енді характеристикалық теңдеуді шешіп, жабайы теңдеуді табайық:

Эллипстің жарты осьтері:

2). Бас диаметрдің теңдеулерін табу үшін, екінші ретті қисықтың центрін табайық:

Бірінші теңдеуді 5-ке, ал екіншісін 4-ке көбейтіп, біріншіден екінші теңдіктің сол жағын алып, мынаны табамыз:

Сонымен, екінші ретті қисықтың центрі БОЛАДЫ.

Енді бас диаметрлердің теңдеулерін табайық:

Сонымен, бас диаметрлер:

3). Абсцисса осінің қандай бұрышқа бұрылғанын мына формула арқылы білеміз:

4). Эллипстің центрін(1,1) анықтап, одан бас диаметрлерді жүргіземіз. Онан кейін эллипстің жарты осьтерін центрден бастап, бас диаметрлердің бойына салып, оның ескі осьтердегі графигін саламыз.(71-сызба).

2-мысал. Екінші ретті сызықтың теңдеуі берілген. Оның графигін саламыз.

Шешуі. Мұның жабайы теңдеуін шығару және оның графигін салу жолы 1-мысалдағыға ұқсас. Бірақ онан айырмашылығы мұнда қисық эллипс емес гипербола болады.

1).

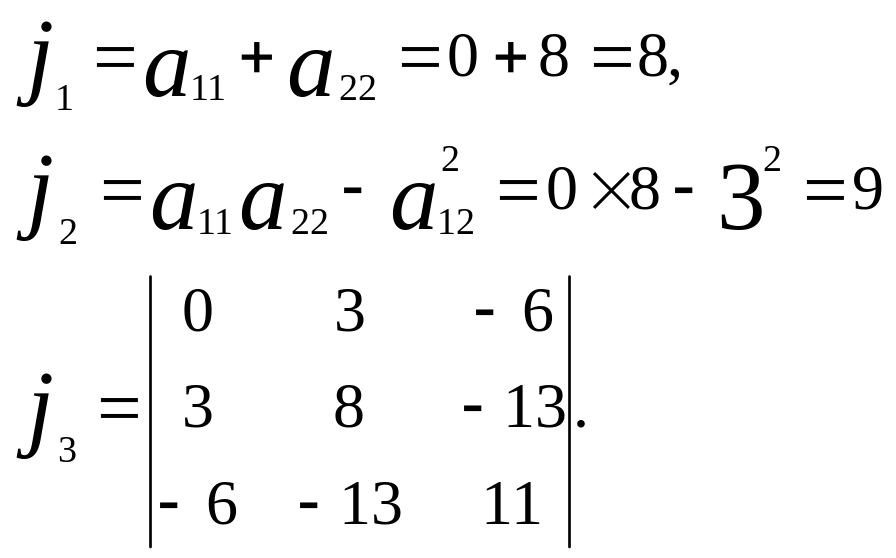
71-сызба.

және болғандықтан, бұл гипербола болады. Ендеше, гиперболаның жабайы теңдеуін іздейміз.

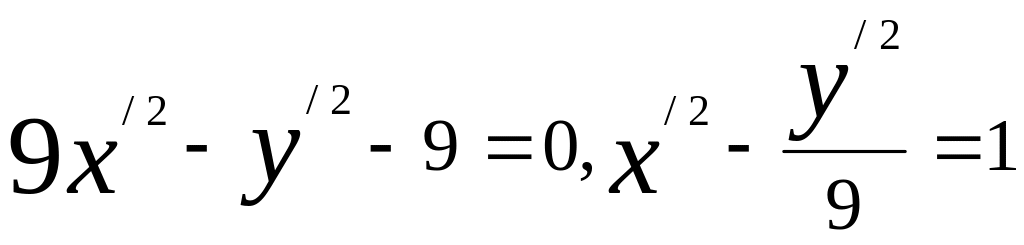
2). Енді осы гиперболаның центрін анықтаймыз.

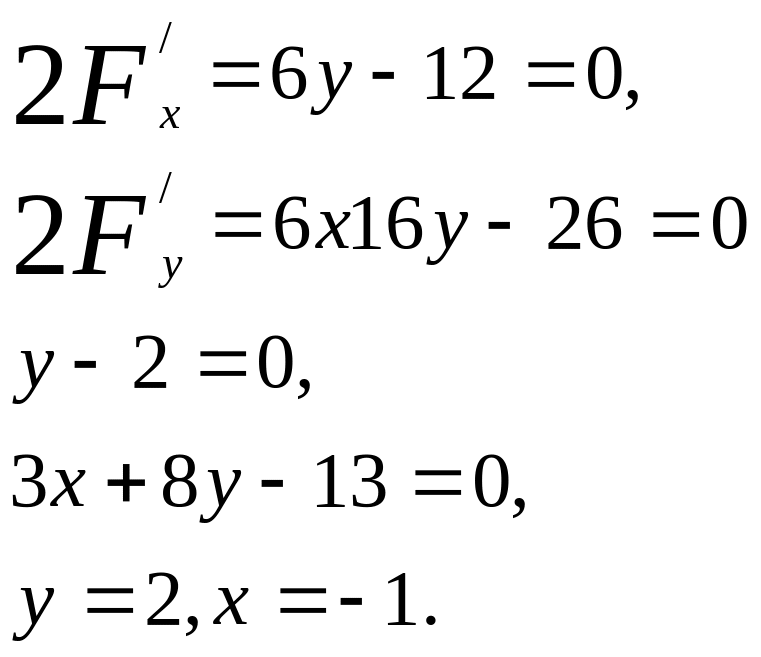
- гиперболаның центрі.

Осы формулаларды қолданып, гиперболаның бас осьтерінің теңдеулерін іздейік. Ол үшін мына анықталған мәндерін: жоғарғы екі теңдеуге қоямыз.