Лекция.
Таќырыбы: Эллипстің, гиперболаның және параболаның канондық теңдеуі. Эллипс пен гиперболаның директрисасы. Эллипстің, гиперболаның және параболанның полярлық теңдеуі.
Эллипс.
Анықтама. Фокустар деп аталатын берілген екі нүктеден қашықтықтардың қосындысы әрқашан тұрақты шама болатын нүктелердің геометриялық орындарын элипис дейді.
Енді элипистің жабайы теңдеуін қорытып шығарайық. Ол үшін анықтамаға сәйкес сызба сызамыз.
Анықтама бойынша:
.
Мұндағы
және
-фокус
деп аталатын берілген нуктелер, М(х,у)-
элипстің бойындағы кез келген нукте,
-тұрақты
шама.
Егер және нуктелерінің ара қашықтығы =2c десек, онда осы екі нүктенің координаталары былай аныкталады:
және
қашықтықтарын
деп белгілесек, онда (1) теңдік мынадай түрде жазылады:
Екі нүтенің ара қашықтығының формуласы бойынша:
Осы
мәндерді
теңдікке қояйық:
Бұл теңдікті түрлендіріп, элипистің жабайы теңдеуін табайық:
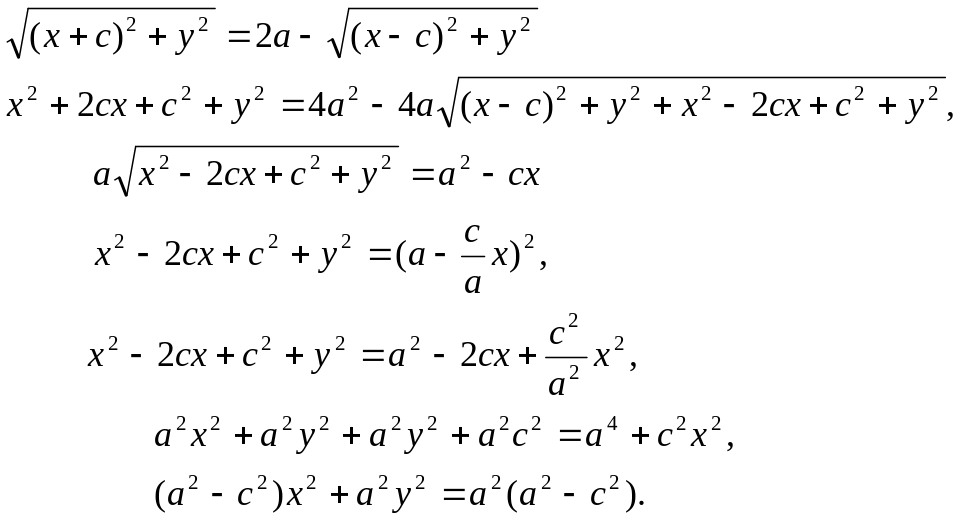
егер
болса,
болады, сондықтан
деп
белгілейік, олай болса
осыдан
Мұндағы
х пен у-элипстің бойындағы кез келген
нүтелердің координаталары, а-элипстің
үлкен жарты осі, b-оның кіші жарты осі.
Бұл теңдеу элипстің жабайы теңдеуі деп
аталады. (3) теңдеудің дәрежесі жұп
болғандықтан, элипстің бойындағы M
нүктесінің координаталары. Әрқашан да
мынадай болады:
. Сондықтан координаталар осьтері
элипске семметриялы, ал семметриялы
осьтердің қиылысқан нүктесі элипстің
центрі болады.
Элипистің түрін оның жабайы теңдеуі бойынша зерттеу
Элипистің
жабайы теңдеуін у арқылы шешейік:
Мұндағы
х пен у-айнымалы шамалар. х-тің мәндеріне
сәйкес у-тің әртүрлі мәндері шығады.
Енді
теңдеуін зерттейік:
1.Егер
х=0 болса, онда
,
яғни
болады. Бұлар кордината осінде жатқан
элипстің бойындағы нүктелер.
2.Егер
болса, онда у=0, яғни
болады. Бұлар абсцисса осінде жатқан
элипстің бойындағы нүктелер.
3.
теңдеуі х-тің барлық нақты мәндерінде
қанағаттанады. Егер х-тің шамасы а-дан
артық болса, онда у жорамал сан болады.
Сондықтан элипстің бойында жатқан
нақты нүктелердің координаталары a мен
b-нің сәйкес шамаларынан артық болмау
керек. Элипстің барлық нүктелері
қабырғалары
және
болатын тік төртбұрышпен шектелген
яғни
және
.
4.
теңңдігінен: a>b, a>c немесе 2a>2b, 2a>2c.
Мұндағы 2a-элипстің үлкен осіне; 2b-элипстің
кіші осі, 2c-элипстің фокустарының ара
қашықтығы.
Элипстің
жабайы теңдеуін зерттегеннен мынадай
қорытынды шығады. Элипс координаталар
системасында өзінің центріне симметриялы
болып орналасатын тұйық қисық сызық
болады. Элипстің центрі координаталар
системасының центрінде жатады.
немесе
.
Егер
мен
нүктелерін қоссақ, онда
тік бұрышты үшбұрыш шығады. Осыдан
Пифогор теоремасы бойынша :
,
осыдан
. Бұл теңдік a,b,c шамаларының өз ара
байланысын көрсетеді.
теңдігінен
екенін көреміз, яғни үлкен жарты ось
әрқашан да фокустың нүктесінен ордината
осінің бойындағы
немесе
нүтесіне дейінгі қашықтыққа тең болады.
нүктелері элипстің төбелері деп аталады.
Радиус-вектор және эксцентриситет.
1-параграфта элипстің жабайы теңдеуін шығарумен байланысты мынадай теңдік шықты:
.
Бұл теңдіктің сол жағы
,
сонда
.
Анықтама бойынша
.
-нің
мәнін осы анықтамаға қойып,
-ді
табайық:
,
.
Сонымен, мынадай екі теңдік шықты:
мұндағы
және
элипстің радиус –векторлары деп
аталады. (4) теңдік осы элипстің
радиус-векторларының формуласы.
қатынасы элипстің эксцентриситеті деп
аталады. Эксцентриситет e әрпімен
белгіленеді.
2-параграфтағы
формуласынан a>c
дегенбіз. Ендеше, элипстің эксцентриситеті
әрқашанда дұрыс бөлшек болады, яғни
e<1 немесе
.
Енді (4) теңдіктегі қатынасының орнына e–ні қойсақ, мынадай теңдіктер шығады:
Егер
абсцисси осіне перпендикуляр болса,
онда
формуласындағы x=c болады.
деп белгілесек, онда
яғни
,
(6) мұндағы p фокальдық параметр деп
аталады.