23. Какие задачи решает графический метод в корреляционном анализе

Графический метод применяют для наглядного изображения формы связи между изучаемыми экономическими показателями. Для этого в прямоугольной системе координат строят график, по оси ординат откладывают индивидуальные значения результативного признака Y, а по оси абсцисс - индивидуальные значения факторного признака X.  Пример: корреляционное поле.

24. Основные требование, предъявляемые к формированию парной корреляционной модели, пояснить их сущность Парная корреляционная модель-это корреляционная зависимость между двумя признаками(результативными и факторными или между двумя факторными). Линейный коэффициент парной корреляции (р) определяется по формуле: где х, у — значения факторного и результативного показателей соответственно; х, у — средние значения соответствующих показателей; σX, σY - средние квадратические отклонения (стандартные отклонения показателей х и у); n — количество наблюдений в совокупности. Значение коэффициента парной корреляции изменяется в пре¬делах от -1 до +1. Знак «+» означает наличие прямой связи между пока¬зателями. Знак «-» — наличие обратной связи. Значение коэффициента от 0 до 1 характеризует степень приближения корреляционной зависи¬мости между показателями и к функциональной. При р = 1 между пока¬зателями существует функциональная связь. При р = 0 линейная связь отсутствует. В целях упрощения расчетов на практике применяются и другие формулы коэффициента парной корреляции, представляющие собой некоторые преобразования исходной формулы.

25. Логический порядок проведения парного корреляционного анализа

Корреляция - это статистическая зависимость между случайными величинами, не имеющая строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой. В статистике принято различать следующие виды корреляции:

парная корреляция - связь между двумя признаками (результативным и факторным, или двумя факторными);

частная корреляция - зависимость между результативным и одним факторным признаками при фиксированном значении других факторных признаков;

множественная корреляция - зависимость результативного и двух или более факторных признаков, включенных в исследование.

1) Построить ранжированный ряд

2)Рассчитать шаг интервала

3) Провести аналитическую группировку 4) Оценить совокупность на однородность

5) Построить корреляционное поле

6) Составить уравнение регрессии, найти неизвестные параметры, с помощью полученного коэффициента регрессии рассчитать теоретические уровни и занести данные в таблицу 7) Рассчитать коэффициент корреляции, детерминации, эластичности.

26. Парная регрессия представляет собой регрессию между двумя переменным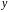и – и .

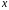Уравнение

Общее y=f(x)

Прямая y=a0+a1

Парабола y= a0+а1х+а2x2

Гипербола y=a0+а1/x

Коэффициенты a0- начало отсчета, значения не имеет

а1-коэффициент регрессии, показывает на сколько в среднем изменяется результативный признак

а2-коэффициент регулирующий регрессию.