3. Элементы теории графов

Теоретические сведения

Граф есть совокупность точек и линий, соединяющих эти точки. Эти соединения могут обладать различными характеристиками, и теория графов занимается изучением этих характеристик.

Пусть задано некоторое конечное множество X, элементы которого будем называть вершинами, и множество V, состоящее из пар элементов (x_i, x_j) множества X. Упорядоченная пара множеств G=(X,V) называется графом. Вершины изображаются точками, а пары элементов – линиями, соединяющими точки, соответствующие образующим пары вершинам [3, 4, 5, 6].

Если в определении графа существенно в каком порядке выбираются вершины (то есть пара (x_i, x_j) отлична от пары (x_j,x_i)), то такой граф называют ориентированным или орграфом, а пару (x_i, x_j) - дугой, при этом считается, что х_i - начальная вершина, a x_j - конечная. В геометрической интерпретации дуге соответствует направленный отрезок. Часто орграф задают парой G=(X, Г), где Х - множество вершин, а Г - неоднозначное отображение, ставящее в соответствие каждой вершине подмножество в X. Г(х_i) - множество вершин х_j Х, для которых в графе G существует дуга (х_i, х_j). Г^l(х_i) - множество вершин х_j X, для которых в графе G существует дуга (x_j, х_i).

Если в определении графа не существенен порядок вершин при образовании пары (х_i, x_j), то граф называют неориентированным или неорграфом, а пару (x_i , x_j) - ребром.

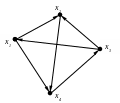
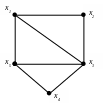
П ример. На рис. 2 изображен ориентированный граф, а на рис. 3 – неориентированный граф.

Рис. 2. Рис. 3.

Путем в графе G называется такая последовательность дуг, в которой конец каждой предыдущей дуги совпадает с началом следующей [5]. Для неорграфа такая последовательность ребер называется цепью. Если путь (цепь) проходит через вершины х₁, ..., х_k то будем обозначать его (ее) символом [x₁, …, x_k].

Для графа на рис. 2 последовательность дуг (x₁, x₂), (x₂, x₄), (x₄, x₃) является путем и может быть обозначена следующим образом [x₁, x₂, x₄, x₃]. Для графа на рис. 3 цепью является, например, следующая последовательность ребер (x₂, x₃), (x₃, x₅), (x₅, x₄), которую обозначим через [x₂, x₃, x₅, x₄].

Маршрут есть неориентированный "двойник" пути, и это понятие рассматривается в тех случаях, когда можно пренебречь направленностью дуг в графе.

Путь (цепь), у которого(-ой) начальная и конечная вершина совпадают, называется контуром (циклом). Для графа на рис. 3 циклом является, например, следующая цепь [x₂, x₃, x₅, x₁, x₂].

Простым циклом графа называется цикл, в котором все вершины различны за исключением начальной и конечной вершины, которые совпадают. Например, для графа на рис. 3 цикл [x₂, x₃, x₅, x₁, x₂] является простым, а цикл [x₂, x₃, x₄, x₅, x₃, x₁, x₂] не является простым.

Петлей называется дуга, начальная и конечная вершины которой совпадают.

Две вершины х_i и х_j называются смежными, если существует соединяющее их ребро (дуга), при этом вершины называются инцидентными этому ребру (дуге), а ребро (дуга) – инцидентным(-ой) этим вершинам. Аналогично, два различных ребра (дуги) называются смежными, если они имеют по крайней мере одну общую вершину [3, 4, 5].

Вершины х₁ и х₄ смежны (рис. 2.), дуга (х₁, х₄) инцидентна вершинам х₁ и х₄, а вершины х₁ и х₄ инцидентны дуге (х₁, х₄). Ребра (х₁, х₃) и (х₃, х₄) смежны (рис. 3).

Число дуг, исходящих из вершины х_i ориентированного графа, называется полустепенью исхода вершины х_i и обозначается . Число дуг, заходящих в вершину х_i ориентированного графа, называется полустепенью захода вершины х_i и обозначается . Так, для орграфа, представленного на рис.2 , .

В неориентированном графе число ребер, инцидентных данной вершине х_i, называют степенью вершины х_i и обозначают d(х_i). Вершина графа, имеющая степень 0, называется изолированной, а вершина, имеющая степень 1 – висячей. Для неорграфа на рис. 3 d(х₁)=3, d(х₃)=4.

Информация о структуре графа может быть задана матрицей смежности. Матрицей смежности графа G=(X,V), |X|=n называется квадратная матрица , элементы которой определяются следующим образом:

Замечание. Матрица смежности неориентированного графа симметрична. В случае кратных ребер a_ij есть количество ребер, соединяющих вершины x_i и x_j. Для орграфа а_ij определяется как количество дуг, направленных от вершины x_i к вершине x_j.

Матрицей инцидентности графа G=(X,V), |Х|=п ,|V|=m называется матрица , элементы которой определяются следующим образом:

е сли G – ориентированный граф, то

если G - неориентированный граф, то

Замечание. Для ориентированного графа петлю, т. е. дугу вида (х_i, х_i) удобно представлять иным значением в строке х_i, например, 2.

Пример. Матричные представления графов проиллюстрированы на рис. 6, 7.

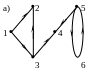
			(1,2)	(1,3)	(3,2)	(3,4)	(5,4)	(5,6)	(6,5)
	1		1	1	0	0	0	0	0
	2		-1	0	-1	0	0	0	0
В=	3		0	-1	1	1	0	0	0
	4		0	0	0	-1	-1	0	0
	5		0	0	0	0	1	1	-1
	6		0	0	0	0	0	-1	1

			(1,2)	(1,3)	(1,5)	(2,3)	(2,5)	(3,4)	(4,5)	(4,6)	(5,6)
	1		1	1	1	0	0	0	0	0	0
	2		1	0	0	1	1	0	0	0	0
В=	3		0	1	0	1	0	1	0	0	0
	4		0	0	0	0	0	1	1	1	0
	5		0	0	1	0	1	0	1	0	1
	6		0	0	0	0	0	0	0	1	1

Рис. 6

а) ориентированный граф и его матрица инцидентности,

б) неориентированный граф и его матрица инцидентности

Рис. 7. Матрицы смежности для графов на рис. 6

Понятия связности и достижимости. Если в графе существует путь, идущий от вершины x_i к вершине х_j, то говорят, что вершина x_j достижима из вершины х_i.

Если для любой пары вершин неориентированного графа существует цепь их соединяющая, то такой граф называется связным. Иначе неориентированный граф называется несвязным.

Ориентированный граф называется сильно связным или сильным, если для любых двух различных вершин x_i и x_j существует по крайней мере один путь, соединяющий x_i с x_j. Это определение означает также, что любые две вершины такого графа взаимно достижимы.

Ориентированный граф называется односторонне связным или односторонним, если для любых двух различных вершин x_i и x_j существует по крайней мере один путь из x_i в x_j или из x_j в x_i (или оба одновременно).

Ориентированный граф называют слабо связным или слабым, если для любых двух различных вершин графа существует по крайней мере один маршрут, соединяющий их.

Если для некоторой пары вершин орграфа не существует маршрута, соединяющего их, то такой орграф называется несвязным.

Пример. Граф, приведенный на рис. 8(а) является сильно связный. Граф, показанный на рис. 8(б), не является сильным, так как в нем нет пути из x₅ в x₂, но односторонне связный. Граф, изображенный на рис. 8(в), не является ни сильным, ни односторонним, поскольку в нем не существует путей от x₅ к x₂ и от x₂ к x₅. Он – слабо связный. Наконец, граф, приведен­ный на рис. 8(г), является несвязным.

Максимальный по включению сильно связный подграф данного графа называется его сильной компонентой связности. Аналогично, односторонняя компонента представляет собой односторонний максимальный подграф, а слабая компонента  максимальный слабый подграф.

Рис. 8. Сильно связный граф (а), односторонне связный граф (б), слабо связный граф (в), несвязный граф (г)

Например, в графе G, приведенном на рис. 8(6), подграф ({х₁, x₄, х₅, х₆}) является сильной компонентой графа G. С другой стороны, подграфы ({х₁, х₆}) и ({х₁, х₅, х₆}) не являются сильными компонентами, хотя и являются сильными подграфами, поскольку они содержатся в графе ({х₁, x₄, x₅, х₆}) и, следова­тельно, не максимальные. В графе, показанном на рис. 4.23(в), подграф ({x₁, x₄, х₅}) является односторонней компонентой. В графе, приведенном на рис. 8(г), оба подграфа ({х₁, х₅, х₆}) и ({х₂, х₃, x₄}) являются слабыми компонентами, и у этого графа только две такие компоненты.

Максимальный связный подграф неориентированного графа G называется компонентой связности.

Максимальный сильно связный подграф ориентированного графа G называется сильной компонентой связности (СК).

М атрица достижимостей графа G=(X,V) , определяется следующим образом:

Множество вершин R(x_i) графа G, достижимых из заданной вершины x_i, состоит из таких элементов x_j, для которых (i, j)-й элемент в матрице достижимостей равен 1. Очевидно, что все диагональные элементы в матрице R равны 1, поскольку каждая вершина достижима из себя самой с помощью, пути длины 0.

Поскольку Г(x_i) является множеством таких вершин x_j, которые достижимы из x_i c использованием путей длины 1 (т. е. Г(x_i) – такое множество вершин, для которых в графе суще­ствуют дуги (x_i, x_j)) и поскольку Г(x_j) является множеством вершин, достижимых из x_j с помощью путей длины 1, то множество Г(Г(x_i))=Г²(x_i) состоит из вершин, достижимых из x_i c использованием путей длины 2. Аналогично Г^p(x_i) является множеством вершин, которые достижимы из x_i с помощью путей длины р.

Так как любая вершина графа G, которая достижима из x_i, должна быть достижима с использованием пути (или путей) дли­ны 0, или 1, или 2, ..., или р (с некоторым конечным р≤n), то множество вершин, достижимых из x_i , можно представить в виде

R(x_i) = { x_i }ÈГ(x_i)È Г² (x_i )È…È Г^p (x_i ) (4.3)

Таким образом, множество R(x_i) может быть получено последова­тельным выполнением (слева направо) операций объединения в соотношении (4.3), до тех пор, пока «текущее» множество не перестанет изменяться при очередной операции объединения. С этого момента последующие операции не будут давать новых элементов множеству и, таким образом, будет получено, достижимое множество R(x_i). Число объединений, которое нужно выполнить, зависит от графа, но, очевидно, что число р меньше числа вершин в графе.

Матрицу достижимостей можно построить так. Находим достижимые множества R(x_i) для всех вершин x_iÎХ способом, приведенным выше. Положим r_ij=1, если x_jÎR(x_i), и r_ij=0 в противном случае. Полученная таким образом матрица R является матрицей достижимостей.

М атрица контрдостижимостей (матрица обратных достижимостей) , определяется следующим образом:

Контрдостижимым множеством Q(x_i) графа G является множество таких вершин, что из любой вершины этого множества можно достигнуть вершину x_i.

Из определений очевидно, что столбец x_i матрицы Q (в котором q_ij=1, если x_iÎQ(x_i), и q_ij=0 в противном случае) совпадает со строкой x_i матрицы R, т. е. Q=R^T, где R^T – матрица, транспонированная к матрице достижимостей R.

Пример. Для графа G, приведенного на рис. 9, найти сильные ком­поненты и построить конденсацию G*.

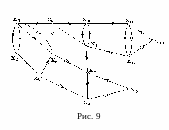
Найдем СК в G, содержащую вершину x₁.

Из соотношений (4.3) и (4.4) получаем

R(x₁) = { x₁ , x₂ , x₄ , x₅ , x₆ , x₇ , x₈ , x₉ , x₁₀ }

Q(x₁) = { x₁ , x₂ , x₃ , x₅ , x₆ }

Следовательно, СК, содержащая вершину x₁, является порожденным подграфом

R(x₁) Q(x₁) = ({ x₁ , x₂ , x₅ , x₆ })

Аналогично, СК, содержащая вершину x₈, есть порожденный подграф ({x₈, x₁₀}), СК содержащая x₇ – подграф ({x₄, x₇, x₉}), СК, содержащая x₁₁, – подграф ({x₁₁, x₁₂, x₁₃ }) и СК, содержащая x₃, – подграф ({x₃}). Следует отметить, что последняя СК со­стоит из единственной вершины графа G. Конденсация G* приведена на рис. 10.

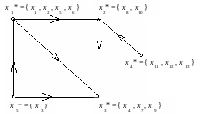
Рис. 10. G* - конденсация графа G

Процедуру, описанную выше и связанную с нахождением СК графа, можно сделать более удобной, если непосредственно исполь­зовать матрицы R и Q. Пусть запись RÄQ означает поэлементное умножение этих матриц. Тогда сразу видно, что строка x_i, матрицы RÄQ содержит единицы только в тех столбцах x_j, для которых выполняется усло­вие: вершины x_i и x_j взаимно достижимы; в других местах строки x_i стоят нули. Таким образом, две вершины находятся в одной и той же СК тогда и только тогда, когда соответствующие им стро­ки (или столбцы) в матрице RÄQ идентичны. Вершины, кото­рым соответствуют строки, содержащие 1 в столбце x_j, образуют множество вершин СК, содержащей x_j. Отсюда мгновенно сле­дует, что матрицу RÄQ можно преобразовать путем транспони­рования строк и столбцов в блочно-диагональную. Каждая из диа­гональных подматриц этой матрицы соответствует СК графа G и содержит только единичные элементы, все остальные элементы блочно-диагональной матрицы равны нулю. Для приведенного ранее примера матрица RÄQ, преобразованная соответствую­щим образом, имеет вид

	x1 x2 x5 x6	x8 x10	x4 x7 x9	x11 x12 x13	x3
x1 x2 x5 x6	1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1	0	0	0	0
x8 R Ä Q = x10		1 1 1	0	0	0
x4 x7 x9	0	0	1 1 1 1 1 1 1 1 1	0	0
x11 x12 x13	0	0	0	1 1 1 1 1 1 1 1 1	0
x3	0	0	0	0	1