7 Силы, действующие на головку балансира ск и их расчет. Формулы а.С.Вирновского и а.Н.Адонина.

В процессе работы штанговой скважинной насосной установки в точке подвеса штанг действуют нагрузки, которые можно раз­делить на

I.Постоянные нагрузки: вес колонны штанг в жидкости Р'_ш;гидростатическая нагрузка Р_ж, обусловленная разницей дав­лений жидкости над и под плунжером скважинного насоса.

II. Переменные нагрузки:

инерционная нагрузка Р_и, обусловленная переменной по ве­личине и направлению скоростью движения колонны штанг;

вибрационная нагрузка Р_виб, обусловленная колебательными процессами в колонне штанг под действием ударного прило­жения и снятия гидростатической нагрузки Р_ж на плунжер;

силы трения, возникающие в результате взаимодействия ко­лонны штанг и насосно-компрессорных труб Р_трм, обтекания пластовой жидкостью колонны штанг Р_трг, взаимодействия плунжера и цилиндра скважинного насоса Р_трпл, перепада дав­ления в клапанах насоса Р_кл, обусловленного их гидравличе­ским сопротивлением.

В общем виде усилия в точке подвеса штанг при ее ходе вверх Р_в и вниз Р_н будут:

Р_в=Р^/_ш+Р_ж+Р_ив+Р_вибв+Р_трм+Р_трг+Р_трпл+Р_клв ,

Р_н=Р^/_ш- (Р_ин+Р_вибн+Р_трм+Р_трг+Р_трпл+Р_клн) .

Р исунок 10.31, а – Идеальная динамограмма работы ШСНУ

Рисунок 10.31, б – Динамограмма работы ШСНУ с учетом упругих

деформаций штанг и труб

Однако работа скважинной насосной установки сопровож­дается значительными периодическими удлинениями колонны штанг λ_ш и труб λ_т (рисунок 10.31, б).

Усилия, действующие в описанном цикле работы, состав­ляют:

вес колонны штанг, погруженной жидкость:

где q_ш - масса 1 м штанг в откачиваемой жидкости, L — глу­бина подвески насоса, λ_ш, λ_ж - удельный вес материала штанг и пластовой жидкости, f_ш - средняя площадь поперечного се­чения колонны штанг.

Вес столба жидкости над плунжером скважинного насоса

Р_ж = F_пл · γ_ж · (L – h) = F_пл· γ_ж ·H =q_ж·Н·g ,

где F_пл - площадь поперечного сечения плунжера, γ_ж - удель­ный вес откачиваемой жидкости, h - погружение насоса под ди­намический уровень, Н - высота подъема жидкости, q_ж - масса 1 м столба жидкости над полной площадью поперечного сечения плунжера.

Для определения сил трения штанг может быть использо­вана приближенная формула

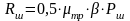,где μ_тр - коэффициент трения между штангами и трубами, мак­симальное значение которого принимают 0,25 - 0,3; β - угол отклонения оси скважины от вертикали, рад.

Сила трения плунжера о цилиндр может быть найдена с по­мощью эмпирической формулы. Р_н = ,

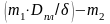где D_пл - диаметр плунжера, м; δ - зазор, мм; коэффициенты т₁ и т₂ принимают значения для обводненных скважин 1,84 и 137, для безводных— 1,65 и 127 соответственно.

Длина хода плунжера относительно цилиндра скважинного насоса представляет собой разность хода точки подвеса штанг и упругих удлинений колонны штанг и труб под действием столба жидкости Р_ж.

А бсолютные упругие удлинения штанг и труб соответственно

, ,

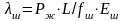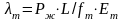где f_ш, f_т - площадь поперечного сечения тела штанг и труб соответственно, Е_ш, Е_т - модуль упругости материала штанг и труб соответственно.

Тогда длина хода плунжера S_пл будет определяться по фор­муле

S_пл = S₀ – (λ_ш – λ_т), где S₀ - длина хода точки подвеса штанг.

Окончательно максимальная нагрузка в точке подвеса мо­жет быть определена по формуле

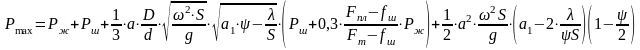
Для расчетов усилий, действующих в колонне штанг, а также в элементах привода имеют значения прежде всего максималь­ное и минимальное усилия, действующие в течение двойного хода штанг, поэтому математическое описание усилий мы огра­ничим приведенной выше формулой А.С. Вирновского.

В результате опытной проверки формул для определения максимального и минимального усилий А. Н. Адониным было установлено, что они с достаточной степенью точности позво­ляют определить эти усилия, и в настоящее время их исполь­зуют как эталонные при проверке результатов, получаемых с помощью других формул.

Работу штанговой скважинной насосной установки А.Н. Адонин предложил разделить на два режима: статический и динамический, и для каждого режима была предложена своя упрощенная формула А.С. Вирновского. Различать режимы он предложил по параметру Коши – отношению частоты вынужденных колебаний штанги к частоте собственных.

Для статического режима работы установки μ = ω∙L/a ≤ 0,35, где а — скорость звука в металле, ω – угловая скорость кривошипа, L – длина колонны

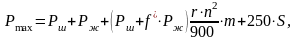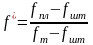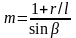где , , β – значение угла φ в момент начала хода штанг вверх; динамический режим при μ > 0,35

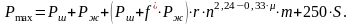
Формула Адонина менее точна, чем Вирновского. Их различие +-100кг.