1.6. Поток вектора напряженности. Электростатическая теорема Гаусса. Теорема Ирншоу.

Э лементарным потоком напряженности электрического поля через малый участок площадью dS поверхности, проведенной в поле, называется физическая величина , где — вектор напряженности электрического поля в точках площадки dS, — единичный вектор, нормальный к площадке dS, — проекция вектора на направление вектора . Поток вектора измеряется в В·м.

Поток вектора напряженности электрического поля через поверхность S равен: .

При этом все векторы нормалей к площадкам dS должны быть направлены в одну и ту же сторону относительно поверхности S. Например, в случае замкнутой поверхности S все векторы нормалей должны быть либо внешними, либо внутренними.

Теорема Гаусса. Поток вектора напряженности электростатического поля в вакууме через произвольную замкнутую поверхность, проведенную в поле, равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на : .

Поверхность интегрирования S называют гауссовой поверхностью.

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью , теорема Гаусса должна быть записана следующим образом: , где интеграл справа берется по объему V, охватываемому поверхностью S.

Теорема Ирншоу: система неподвижных точечных электрических зарядов, находящихся на конечных расстояниях друг от друга, не может быть устойчивой. Теорема Ирншоу показала, что атомы и молекулы представляют собой не статистические, а динамические системы заряженных частиц.

1.7. Применение теоремы Гаусса к расчету электростатических полей.

Напряженность поля бесконечной равномерно заряженной плоскости .

Н апряженность поля внутри двух параллельных бесконечных плоскостей (плоского конденсатора), заряженных разноименно с одинаковой по величине постоянной поверхностной плотностью: .

Напряженность поля бесконечной равномерно заряженной нити , где — расстояние от нити до точки, в которой измеряется напряженность.

Напряженность поля полого равномерно заряженного по поверхности цилиндра: 1) если , то ; 2) если , то , где R — радиус цилиндра.

Н апряженность поля заряженной сферы: 1) если , то ; 2) если , то , где R — радиус сферы, - полный заряд сферы.

Напряженность поля внутри шара, равномерно заряженного по объему: . Вне шара напряженность убывает по такому же закону, как и у поля точечного заряда.

1.8. Работа электростатических сил.

Работа , совершаемая кулоновскими силами при малом перемещении точечного заряда в электростатическом поле, равна , где Е — напряженность поля в точке нахождения заряда q.

Работа кулоновских сил при конечном перемещении заряда q из точки 1 в точку 2 равна: .

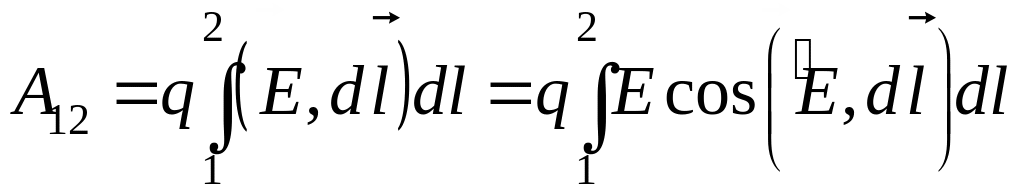Для точечного заряда q в вакууме работа по его перемещению из точки 1 в точку 2 в поле другого точечного заряда равна: 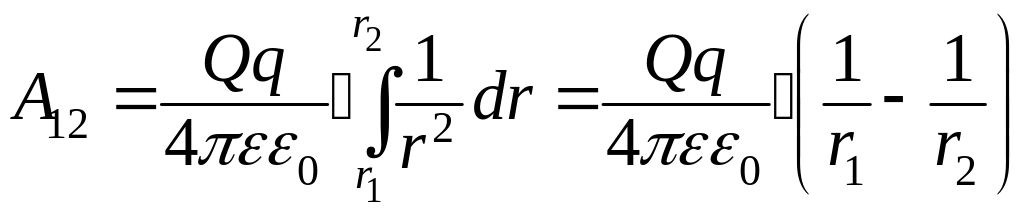,где - расстояния соответственно от точек 1 и 2 до заряда Q.

Для одноименных зарядов Q и q работа кулоновских сил отталкивания положительна, если заряды удаляются друг от друга, и отрицательна, если заряды сближаются.

Работа сил электростатического поля при перемещении заряда из точки 1 в точку 2 не зависит от формы траектории заряда .

Работа сил электростатического поля при перемещении заряда вдоль любого замкнутого контура равна нулю, так как в этом случае .

Таким образом, электростатическое поле является потенциальным полем.

Потенциалом электростатического поля в данной точке называется отношение потенциальной энергии пробного заряда , находящегося в некоторой точке поля, к величине этого заряда: .

Потенциалом электрического поля точечного заряда называется величина, равная работе по переносу единичного поло­жительного заряда из данной точки пространства на бесконечность: .

Потенциал электрического поля заряженной сферы радиусом R равен: 1) при ; 2) при , где - заряд сферы.

Работа по перемещению единичного заряда в поле точечного заряда равна разности потенциалов заряда в данном поле: .
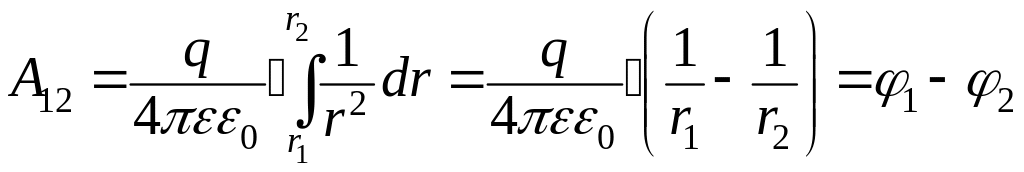