Глава 6

Изгиб

§1 Понятие изгиба. Нейтральная линия.

О пределение: Изгибом называется вид деформации, при котором происходит искривление оси бруса. В дальнейшем будем рассматривать деформацию плоского прямого изгиба, при котором силовая плоскость проходит через одну из главных центральных осей сечения.

К роме прямого, может возникать косой изгиб, при котором силовая плоскость совпадает только с одной центральной осью, т.е. происходит под некоторым углом к главным центральным осям.

В зависимости от возникающих в балке внутренних силовых факторов (ВСФ) различают чистый и поперечный изгиб (рис. 6.3).

Чистым изгибом называется изгиб, при котором в сечении балки возникает только изгибающий момент, а поперечным называется изгиб, при котором действуют как изгибающий момент, так и поперечная сила.

В общем случае при изгибе часть слоев (волокон) бруса удлиняется, а другая часть укорачивается, т.е. в этих волокнах возникает деформация растяжения или сжатия соответственно (рис. 6.4). При этом существует такой слой, называемый нейтральным, длина которого не изменяется, хотя слой искривляется. В поперечном сечении бруса этот слой характеризуется нейтральной линией.

К ак показывают расчеты нейтральная линия проходит через главную центральную ось сечения, расположенную перпендикулярно к силовой линии.

Нейтральную линию иногда называют нулевой линией, т.к. в ее точках нормальные напряжения и продольные деформации отсутствуют (σ = 0; ε = 0).

§2 Напряжения при чистом и поперечном изгибе.

Основное условие прочности.

В теории изгиба принимаются такие допущения:

1) Справедлива гипотеза плоских сечений.

2) По высоте сечения бруса волокна не имеют веса, т.е. не давят друг на друга. Принимается упрощенная схема напряженного состояния.

3 ) по ширине сечения бруса напряжения являются постоянными.

С учетом принятых допущений и рассматривая четыре стороны задачи для чистого изгиба, при котором возникают только нормальные напряжения можно использовать следующую расчетную зависимость.

г де σ(y) – нормальные напряжения в точке

сечения бруса, находящейся на

расстоянии y под нейтральной

линией.

M_изг – изгибающий момент в данном

сечении

I_x – осевой момент инерции сечения

относительно

y – ордината последней точки.

Анализируя зависимость (15.1) можно заключить, что нормальное напряжение изменяется по линейному закону, увеличиваясь от центра сечения к его краям. Причем максимальные напряжения, возникающие в крайних волокнах можно определить по известной формуле:

где – осевой момент сопротивления [м³].

Зависимость (15.1) и (15.2) графически можно представить в виде следующей эпюры напряжений (рис. 6.8).

П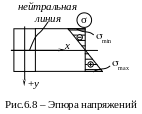 ри проектировании балочных конструкций целесообразно применять профили, имеющие рациональную форму с точки зрения полученной эпюры напряжений. Считается, что профиль (или сечение), у которого большая часть материала располагается в крайних волокнах является рациональным. Например, двутавр, швеллер, пустотелый прямоугольник, сдвоенный уголок.

Расчет на прочность при чистом изгибе производится по следующему условию прочности

Условие (15.3) является основным условием прочности при изгибе. При помощи этого условия можно выполнить известные виды расчетов: проверочный, проектировочный и максимальной нагрузки.

– проверочный по (15.3)

– проектировочный

– расчет грузоподъемности

При расчете на прочность балок из разных материалов необходимо учитывать их способность сопротивляться растягивающим и сжимающим напряжениям. При этом следует придерживаться следующих рекомендаций:

1. Если балка изготовлена из пластичного материала, одинаково работающего на растяжение-сжатие, т.е. ([σ_р] = [σ_c]), то целесообразно использовать сечения, симметричные относительно нейтральной линии. В этом случае на прочность проверяются крайние точки сечения балки σ_max = |σ_min| (рис.6.9).

2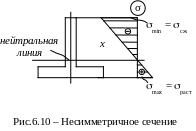 . Если материал балки хрупкий, лучше работающий на сжатие, чем на растяжение ([σ_р] < [σ_c]), то целесообразно выбрать сечение несимметричное относительно нейтральной линии, причем его необходимо располагать так, чтобы в растянутых волокнах напряжения были бы меньше по абсолютному значению, чем в сжатых волокнах (рис. 6.10).

Напряжения при поперечном изгибе

Р ассмотрим напряжения, возникающие при поперечном изгибе. В этом случае нарушаются ранее принятые допущения, названные гипотезой плоских сечений, т.е. при поперечном изгибе сечения балки плоскими не остаются, т.к. происходит смещение волокон балки по высоте.

Указанное смещение продольных волокон балки вызывается касательными напряжениями, которые возникают как в поперечных, так и в продольных сечениях балки (на основании закона парности касательных напряжений).

При поперечном изгибе нормальные напряжения произвольной точки балки можно определить по формуле чистого изгиба

Касательные напряжения при поперечном изгибе находятся по формуле Журавского Д.И. (1855 год):

г де τ_y – касательные напряжения в точке сечения балки, расположенной на расстоянии y от оси x (от нейтральной линии).

Q_y – поперечная нагрузка вертикальной плоскости, действующая в данном сечении (знак Q = знак τ, т.е. знак Q определяет знак касательных напряжений).

 – статический момент относительно оси x части сечения, отсекаемой заданным уравнением и ближайшим крайним волокном сечения.

I_x – осевой момент инерции всего сечения относительно оси x (нейтрального слоя).

b_(y) – ширина сечения на уровне рассматриваемой точки (с учетом имеющихся пустот).

А нализ зависимости (16.2) показывает, что при поперечном изгибе максимальные касательные напряжения будут возникать на уровне нейтрального слоя.

При поперечном изгибе касательные напряжения имеют заметную величину для коротких балок с большой высотой сечения h>>l, в противном случае этими напряжениями можно пренебрегать.