Федеральное агентство морского и речного транспорта

Федеральное бюджетное образовательное учреждение высшего

профессионального образования

« Волжская государственная академия водного транспорта»

«Утверждаю»

Зав. Кафедрой

____________/Г.Е.Онянов/

« » _______________ 20011г.

Ст. пр. В.П. Абраменкова

Математика

Краткий курс лекций

Пермь, 2011г.

1. Цель, предмет и задачи дисциплины

«Математика» является основной дисциплиной цикла математических и естественнонаучных дисциплин.

Цели изучения дисциплины состоят в овладении студентами:

• базовыми знаниями в области математики как основы фундаментальных знаний;

• навыками решения задач;

• навыками самостоятельной работы с математической литературой.

Целью изучения также является формирование научного мировоззрения студентов.

Предмет дисциплины составляют основные понятия, определения, теоремы разделов математики и методы решения задач.

Задачи дисциплины состоят в обучении студентов:

• основным понятиям, определениям и теоремам разделов математики;

• умениям использовать полученные знания при решении задач и изучении общенаучных дисциплин и дисциплин специальности;

• умениям использовать систему знаний дисциплины для адекватного математического моделирования различных, в том числе экономических, процессов.

2. Требования к уровню освоения дисциплины

В результате изучения дисциплины «Математика» студент должен:

а) иметь представление об основах: линейной алгебры; аналитической геометрии на плоскости и в пространстве; анализа бесконечно малых величин; дифференциального исчисления функций одной переменной; дифференциального исчисления функции нескольких переменных; интегрального исчисления функции одной и нескольких переменных; дифференциальных уравнений; теории рядов; теории вероятностей и математической статистики.

б) знать: основные понятия, теоремы, методы и правила решения типовых задач изучаемых разделов математики.

в) уметь: применять математические методы к решению теоретических и практических задач; применять полученные знания для решения задач общенаучных и специальных дисциплин.

г) приобрести навыки в решении задач и оценки полученных результатов.

д) владеть, иметь опыт использования необходимых вычислительных средств, таблиц и справочников при производстве расчётов.

Тезисы лекций элементы линейной алгебры

1. Матрицы

Прямоугольная таблица чисел, содержащая т строк и п столбцов, называется матрицей размера тх п: .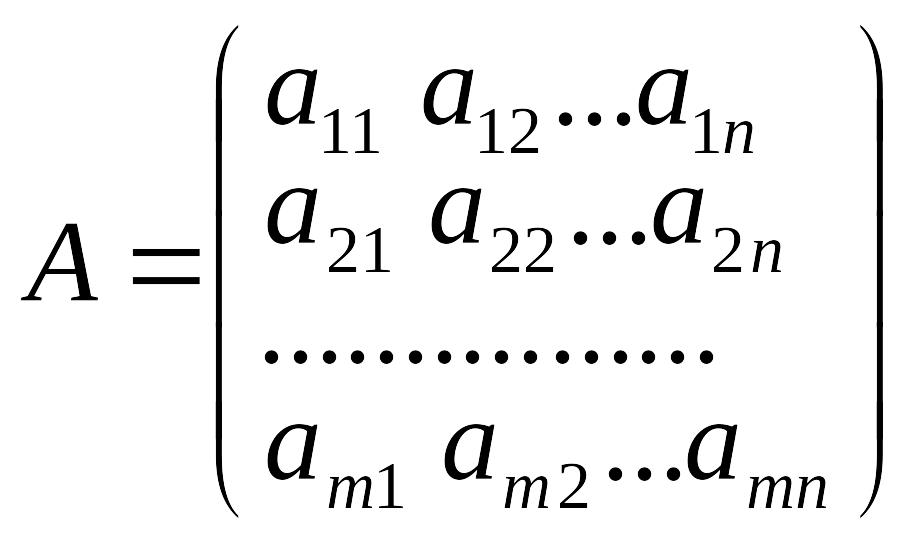

Каждый элемент матрицы снабжается двумя индексами: первый указывает номер строки, а второй – номер столбца, в которых расположен этот элемент.

Две матрицы называются равными, если числа их строк и столбцов совпадают и если равны элементы, расположенные на соответствующих местах этих матриц.

Если число столбцов матрицы п равно числу ее строк, то матрицу называют квадратной матрицей порядка п. Элементы квадратной матрицы порядка п образуют ее главную диагональ.

Квадратная матрица называется диагональной, если все ее элементы, расположенные вне главной диагонали, равны нулю. Диагональная мат­ица называется единичной, если все ее элементы, расположенные на главной диагонали, равны единице.

Матрица называется транспонированной для матрицы А если она получена из матрицы А путем перестановки местами строк и столбцов.

Действие над матрицами:

1) Умножение матрицы на число. Чтобы умножить матрицу на число, надо каждый элемент матрицы умножить на это число.

2) Сложение матриц. Суммой матриц А и В одинаковых размеров называется матрица, элементы которой равны суммам элементов матриц А и В, расположенных на соответствующих местах.

3) Умножение матриц. Матрицу А можно умножить на матрицу В только в том случае, когда число столбцов матрицы А равно числу строк матрицы В. В результате умножения получится матрица С, у которой столько же строк, сколько их матрице А, и столько же столбцов, сколько их в матрице В, а элементы матрицы С вычисляются по формуле:

,

т.е. для получения элемента , расположенного в i-строке и j-ом столбце матрицы С, надо элементы i-ой строки матрицы А умножить на соответ­ствующие элементы j-го столбца матрицы В и полученные произведения сложить.