Міністерство освіти і науки України

Ковельський промислово-економічний коледж Луцького НТУ

Основи технічної механіки

Методичні вказівки

Опорний конспект лекції для студентів

спеціальності 5.07010102«Організація перевезень і управління на автотранспорті»

Ковель 2014

Основи технічної механіки. Методичні вказівки. Опорний конспект лекції для студентів спеціальності 5.07010102 «Організація перевезень і управління на автотранспорті». Шовкович О.В., Селівончик Т.В., Ковель: КПЕК Луцького НТУ, 2014 рік. –

Методичні вказівки. Опорний конспект лекції містять матеріал для поглибленого вивчення, самоконтролю та контролю знань студентів спеціальності 5.07010102 «Організація перевезень і управління на автотранспорті».

Укладачі: Селівончик Т.В. к.т.н., Шовкович О.В.

Рецензент: Бабарика С.Ф. к.т.н.

Відповідальний за випуск: Борисюк Л. В., методист.

Затверджено науково-методичною радою КПЕК Луцького НТУ, протокол

№ ___ від _____________ 2014 року.

Затверджено до друку науково-методичною радою

Л уцького НТУ, протокол № від_____________2014року

Тема: Просторова система сил.

1.Паралепіпед сил.

2.Рівнодіюча просторової системи збіжних сил. Момент сили відносно осі.

3 Головний Вектор і головний момент .

4. П’ять рівнянь рівноваги просторової системи сил.

5. три рівняння рівноваги просторової системи паралельних сил.

6. Застосування рівнянь рівноваги.

1

В статики приходиться вивчати приведення і рівновагу системи , нерозміщених в одній площині, так званих просторових систем сил.

1. Система декількох сил, лінії дії, які лежать в одній площині , але але перетинаються в одній точці наз. Просторовою системою збіжних сил.

Так само як і у плоску систему збіжних сил, таку систему можна звести до систем сил прикладених в одній точці . Нехай в точці О (мал. 93) прикладено декілька сил, які не лежать в одній площині наприклад сили

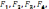ці сили не лежать в одній площині , але попарно кожні 2 із них лежать в якій-небудь одній площині , так як через 2 любі перетинаючи прямі завжди можна провести площину , і при тому тільки одну. Таким чином для складання 2-ох яких-небудь сил такої системи , наприклад для складання сил 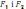ми можемо застосувати правило складання збіжних сил на площині і знайти рівнодіючу 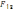прикладену в тій самій т. провівши площину через цю рівнодіючу і яку-небудь 3-тю силу 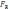, ми можемо знайти по тому правилу трикутника рівнодіючу 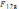трьох сил ітд.

Як видно з мал. 1 рівнодіюча просторової системи збіжних сил зображається по модулю і по напрямку замкнутої сторони многокутника ( OABC) побудованого на складених силах , т.е. являється їх геометричною сумою = 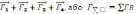(35)

Момент сили відносно якої-небудь осі наз. величина ,характеризуюча обертовий ефект даної сили відносно однієї осі .

Почнемо з конкретного приклада

Представимо що сила F прикладена до тіла , яке може обертатися кругом нерухомої осі , наприклад двері , обертаються на петлях кругом осі z ( мал. 102) , не лежать в площині перпендикулярної до цієї осі.

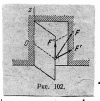
Ясно що F даної сили паралельна осі обертання тіла , не може відповісти йому обертовим рухом Ця вила прагне тільки зрушити тіло по осі z обертовий ефект визиває лежачу в площині перпендикулярну до осі обертання тіла F являється проекцією сили F на площину , перпендикулярну до осі обертання тіла . Послідовно обертовий ефект діючої сили F відносно осі z , відносно точки січення О осі з вказаною площиною. Цей момент називається моментом сили F відносно осі.

2. Так , момент сили відносно осі рівний моменту проекції цієї сили на площину , перпендикулярну до даної осі , відносно точки січення осі з площиною.

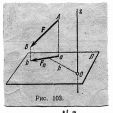
Визначимо момент сили F відносно вісі силам 1 z(F ) . Модуль проекції сили F на перпендикулярну вісь z площина - символ . Плече цієї проекції відносно точки січення осі з площиною – символом h будемо мати :

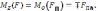(40).

Цей чи інший знак в цієї формулі обчислюється по слідую чому правилу : якщо для спостерігача, який дивиться на площину П із додатньо х сторони осі z (вказаною стрімкою ).

Проекція сили F на площину П представлена обертатися кругом осі z поти годиникової стрілки , то момент буде додатнім , якщо навпаки – відємним.

Момент сили відносно осі обчислюється своїм числовим значенням і знаком являється , послідовно скашеркою алгебраїчною величиною .

Замітимо що : момент сили відносно даної осі не зміниться , якщо перенести сили повздовж , так як при цьому не зміниться ні проекція сили на дану площину , не на її плече . Момент сили відносно осі рівний нулю , якщо лінія дії сили і вісь лежать в одні площині . При цьому можливі 2 випадки : 1) сила паралельна осі . В цьому випадку рівна нулю проекції сили на площину перпендикулярну до осі. 2) лінія дії сили пересікає вісь . тоді проекція сили на площину проходить через точку січення осі з площиною і її плече відносно цієї точки рівне нулю .

Так як пара ні при яких умовах не може бути врівноважена однією силою , то для рівноваги довільної просторової системи сил необхідно тихже двох загальних умов , що і для рівноваги довільної плоскої системи сил.

3. Для рівноваги системи сил , розміщені як не будь в просторі , необхідно щоб рівнялися нулю головний вектор 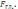і головного моменту МГА . довільно обратного центра зведення .

Цими умовами можна подати і більш кращу для практичних цілей аналітичну форму. Із формул для модулів головного вектора і головного моменту МГА. Просторової системи сил , що вони перетворюються в нуль в тому випадку , коли мають місце слідуюче рівняння:

∑

∑

∑

∑

∑

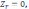
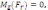∑ (41).

Для рівноваги системи сил , розміщені де – не будь в просторі необхідно , щоб окремо рівнявся нулю суми проекцій всіх сил на кожну із трьох довільно вибраних але щоб не лежали в одній площині координатних осей і суми моментів всіх сил відносно кожної із трьох таких осей.

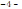
Користуючись рівняннями рівноваги сил розміщених де-небудь в просторі , можна знайти рівняння рівноваги просторової системи паралельних сил .

Нехай ми маємо систему паралельних сил .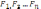

Так як вибір координатних осей довільний то візьмемо вісь z , яка паралельна данаї системи сили. Складемо 6 рівнянь довільної просторової системи сил . так так як осі x та y перпендикулярні до даним паралельним силам , то проекції у перпендикулярів до даним паралельним силам то проекції на ці осі кожної із сил даної системи будуть рівні нулю.

Послідовно при такому виборі координатних осей рівняння задовільняють незалежно від того , чи знаходиться система в рівновазі чи ні , а тому перестають бути умовами рівноваги. Ак як всі дані сили паралельні осі z , то їх проекції на цю вісь рівні модулям цих сил, взявши зі знаком мінус чи плюс в залежності від того , в яку сторону вони напрямлені. Послідовно рівняння 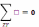, можна замінити рівнянням ∑( ) =0. Відпадає також рівняння ∑ 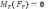так як моменти всіх сил відносно паралельної осі z будуть завжди окремо рівні нулю при різному значенні сил і різної їх відстані від осіz.

Таким чином , для системи паралельних сил залишаються тільки 3 рівняння рівноваги .

∑( ) =0 , ∑ 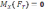, ∑ . (42)

Для рівноваги просторової системи паралельних сил , необхідно щоб рівнялися нулю алгебраїчна сума всіх сил відносно кожної із двох осей , які належать в площині перпендикулярної до даними паралельними силами.

Е.М. Никитин « Теоретическая механика» 1986 г.

Параграфы: 39-41, стр. 126-137.

Не тільки своїм численним значенням а й своїм правленням прямком на площину проекції. По Модулю проекції вектора на площину ( мал. 97)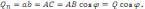

де - кут між напрямком вектора Q напрямком його проекції на площину .

Напрямком цієї сили обчислюється із формул ,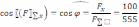

,

,

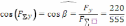В результаті отримаємо 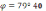, , і .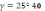

Задача 39.

Стержень СД одним кінцем шарнірно закріплений до вертикальної стіни . Другий його кінець підтримується двума горизонтальними ланцюгами однакової довжини .

АД і ВД , прикріпленими до тої ж стіни. На кінці кінці Д підвішений вантаж G=1 кH.

Знайти силу зжимаючу стержень і натяг ланцюгів , якщо 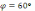і .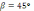

Рішення .

Сила G тяжіння вантажа діє на т.д . Ця точка не вільна ,зв’язками служить стержень СД і ланцюг АД і ВД.

Звільняємося від цих зв’язків , замітивши їх реакціями N ( стержня ) і 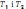(ланцюгів АД і ВД).

Для того щоб знайти момент деякої сили F відносно на площину ( П) , перпендикулярну до вісі z, і взяти момент цієї проекції відносно точки січення вісі з площиною.

Плоска система довільно розміщених тіл

1. Види опор балочних систем :

а) вільне опирання ,

б) шарнірно - рухома опора,

в) шарнірно - нерухома опора,

г) жорстке защемлення

2. Класифікація навантажень.

3. Зауваження до рішення задач на рівновагу

плоскої системи сил.

Раціональний вибір напрямку координатних

осей і центру моментів при рішенні задач.

В техніці часто використовують системи, які можна представити у

вигляді балок.

Балками називають бруси з прямолінійною віссю, покладені на опори.

Балки служать для передачі діючих навантажень на опори.

Розрізняють такі опори :

Шарнірно - рухома опора.

Така опора накладає на балку тільки один зв’язок, залишаючи їй лише одну

вертикальну реакцію ( можливість рухатись за напрямком осі y ).

Переміщенню вздовж осі x і обертанню навколо шарніра така опора не

перешкоджає.

Рухомий шарнір замінюється лише однією реакцією y, невідомою по величині.

Реакція y може бути направлена до опори і від опори.

Вільне опирання.

Ця опора залишає балку з однією реакцією зв’язку—можливість переміщуватися відносно осі y.

Активні сили завжди повинні прижимити балку до опори. Реакції y при вільному опиранні повинна бути напрямлена завжди тільки від опори.

Шарнірно-нерухома упора.

Така опора накладає на балку два зв’язки, не даючи їй можливості рухатись ні по осі x, а по осі y, але залишає їй одну степінь свободи обертання навколо шарніру. Реакція шарнірно-нерухомої опори заміняється двома змістовними, невідомими по величині x та y.

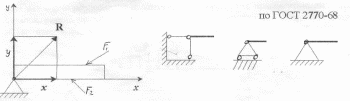
Жорстке защемлення.

Ця опора обмежує балку всіх трьох степенів свободи: лінійних переміщень вздовж осей x та y і можливості обертання . В зарубці з’являються три невідомих реактивних зусилля: вертикальна реакція y, горизонтальна реакція x і реактивний момент заробки М₃.

(Вільне тіло на плоскій поверхні має 3 незалежних рухи: переміщення вздовж осей xта yта обертання навколо якоїсь точки, тобто на плоскій перхні воно має 3 степені свободи).

Балки, які мають опори, в яких загальне число невідомих реакцій дорівнює числу рівняння рівноваги, являються статистично визначними.

2.Навантаження.

Розрізняють 3 степені навантажень: зосереджені, розподілені і моментні.

Зосередженим навантаженням називають силу, прикладену до будь-якої точки твердого тіла.

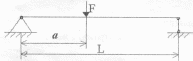
Розподіленим навантаженням називають сукупність сил, розподілених згідно будь-якого закону по довжині (площі, об’єму тіла).

Навантаження на одиницю довжини називають інтенсивністю та позначають /L (н/м).

Рівномірно розподілене навантаження зображають прямокутником з сіткою стрілок, висота прямокутника відповідає інтенсивності q, а ширина l- довжині навантаженої частини.

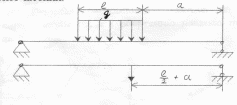
При рішенні задач таке навантаження замінюють зосередженою силою Qчисельно рівною площі заштрихованого прямокутника Q=q∙ɭі прикладеної всередині навантаженої частини.

Моментним навантаженням називають пару сил, момент якої задається модулем М, а напрям – стрілкою. На схемі таке навантаження позначають або парою сил, або дугою зі стрілкою, що вказує напрямок дії моменту.

Тема 1004.Плоска система довільно розміщених сил.

Заняття 3.

План.

1. Зв’язки з тертям

2. Сила тертя, кут тертя, коефіцієнт тертя .

3. Умова самогальмування , конус тертя

1. Тертям називають опір,що виникає при переміщенні одного тіла по поверхні другого .

В залежності від характеру переміщення ( від того ковзає тіло чи котиться ) розрізняють два вида тертя:

1. тертя ковзання , чи тертя 1-шого роду;

2. тертя кочення , чи тертя другого роду

Прикладами тертя ковзання можуть бути: тертя пилки по дереву , підошви взуття по землі , втулки колеса по вісі і т.д. Прикладами тертя кочення є тертя при перекочуванні коліс автомобіля по землі чи вагона по рельсам, тертя при перекочуванні круглих полін, тертя при перекочуванні коліс автомобіля по землі чи вагона по рельсам , тертя при перекочуванні круглих полін , тертя в кулькових і роликових підшипниках і т.д.

Тертя ковзання – це опір ковзанню одного тіла по поверхні іншого .

Тертя кочення – це опір перекочуванню одного тіла по поверхні іншого .

2.Головною причиною тертя ковзання є те , що поверхні тіл , що контактують не є абсолютно гладкими , а більше чи менше жорсткі , в результаті силу для подолання опору мікроскопічних нерівностей цих поверхонь. Прикладання сили потрібне і для подолання молекулярної взаємодії між частинками поверхневих шарів тіл , що торкаються . Сила тертя в тій чи іншій мірі горизонтальною силою F , для чого прив’яжемо до нього нитку та , перекинувши її кінця чашку з гирям (рис.1) Брусок лишиться нерухомим до тих пір поки модуль сили Fне досягне деякого значення. Це показує , що на тіло крім ваги Gта нормальної реакції Rf , рівна по модулю і протилежна силою тертя , що виникає між поверхнями бруска і опорною площиною. З збільшенням вантажу брусок буде лишатись в стані спокою до тих пір , поки сила Fне стане рівною чи більшоюRf , тобто FRF.

Сила тертя що виникає при відносному спокою тіла називається тертям спокою,сила тертя,що діє при ковзані тіл , називається тертям руху .

На основі багато чисельних дослідів Кулон встановив наступні закони :

1. Сила тертя не залежить від розмірів поверхонь тертя.

2. Максимальна сила тертя прямо пропорційна нормальній складовій зовнішніх сил, що діють на поверхні тіла.

3. Сила тертя залежить від матеріалу тіл, стану поверхонь тертя, наявності і виду мастила.

4. Сила тертя при русі менша за силу тертя спокую.

Якщо Rf-максимальне значення тертя спокою, а Rn- нормальна реакція опорної поверхні, то на основі даного закону будемо мати:

Rf=fRn

Де f- коефіцієнт пропорційності, який називається коефіцієнтом тертя спокою.

Досліди показали, що при збільшенні швидкості ковзання до певної межі, сила тертя зменшується. Значить сила тертя при русі можна визначити по формулі Rf=f*Rn

Де f- коефіцієнт тертя при русі.

Коефіцієнти тертя для різних матеріалів різні. В грубих розрахунках часто не роблять різниці між коефіцієнтами руху спокою та беруть коефіцієнт тертя руху.

Найбільший кут, на який за рахунок тертя від нормалі реакції Rшорсткий поверхні, називається кутом тертя tg=Rf/Rn=f.

Отже тангенс кута тертя рівний коефіцієнту тертя ковзання.

3. Якщо ми розглянемо тіло, що має можливість переміщуватись по шершавій поверхні в любому напрямку, то лінії дії можливих реакцій R цієї поверхні утворять конічну поверхню (рис. 4 ). Конус твірні якого нахилені під кутом тертя до поверхні ковзання в даній точці називається конусом тертя.

Якщо сила тертя спокою неповна, то відношення f=Rf/Rn=Fт/n називають коефіцієнтом зчеплення, де Fт- сила тертя, N- нормальна реакція.

Якщо для різних напрямків руху тіла по поверхні (дерево) коефіцієнт тертя неоднаковий, то конус тертя буде овальний. Властивість конуса полягає в тому, що для рівноваги тіла,яке лежить на жорсткій поверхні, рівнодіюча прикладених до нього активних сил має проходити в середині конуса тертя. Для того щоб тіло знаходилось в стані спокою на похилій поверхні необхідно щоб нахилу поверхні тіла був менший за кут тертя.