Примеры решения задач

1. Молекулярно-кинетическая теория идеальных газов

Задача 1. Определить, сколько киломолей и молекул водорода содержится в объеме 50 м³ под давлением 767 мм рт. ст. при температуре 18°С. Какова плотность и удельный объем газа?

Дано: V = 50 м3 Ρ = 767 мм. рт. ст.  767·133 Па Т = 291 К М = 2 кг/моль	Решение: На основании уравнения Менделеева – Клайперона: устанавливаем число киломолей ν, содержащихся в заданном объеме V. Зная р - давление, V – объем, Т – температуру газа, R – молярную газовую постоянную
ν – ? N – ? ρ – ? d – ?

можно определить ν:

Число молекул N, содержащихся в данном объеме, находим, используя число Авогадро N_А (которое определяет какое количество молекул содержится в одном киломоле). Общее количество молекул, находящихся в массе m данного газа, может быть установлено, так как известно число молей ν.

Подставляя в формулу число киломолей, устанавливаем число молекул, содержащихся в объеме V: .

Плотность газа ρ = m/V определяем из уравнения Менделеева - Клайперона:

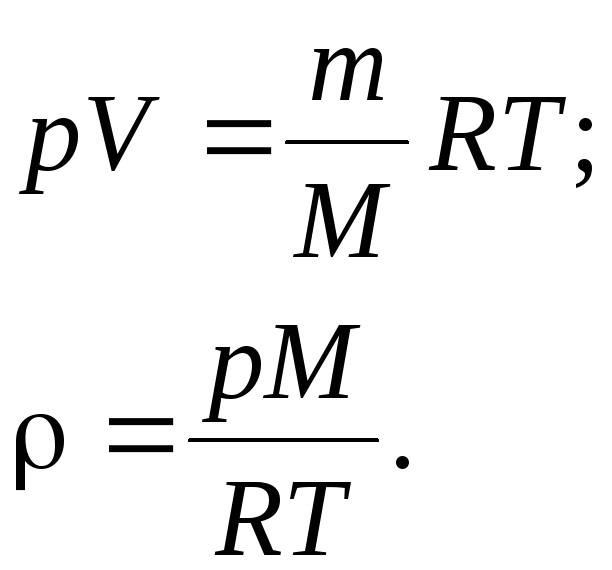
Подставляя числовые значения в единицах СИ в формулу, определим плотность газа:

Удельный объем газа d определяем из уравнения Менделеева - Клайперона:

(м³/кг).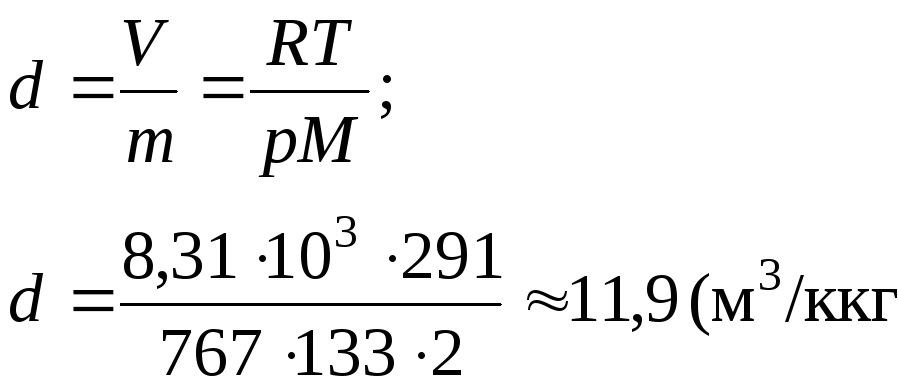

Ответ: 11,9 м³/кг.

Задача 2. В сосуде объемом 2 м³ находится смесь 4 кг гелия и 2 кг водорода при температуре 27°С. Определить давление и молярную массу смеси газов.

Дано: V = 2 м3 m1= 4 кг М1= 4·10-3 кг/кмоль m2= 2 кг М2= 2·10-3 кг/кмоль Т1= 300 К	Решение: Воспользуемся уравнением Менделеева - Клайперона, применив его к гелию и водороду: (1) (2) где р1 – парциальное давление гелия; m1 – масса гелия;
р - ? М - ?

М₁ – его молярная масса; V – объем сосуда; Т – температура газа; R = 8,31 Дж/(моль·К) –молярная газовая постоянная; р₂ – парциальное давление водорода; m₂ – масса водорода; М₂ – его молярная масса.

По закону Дальтона: (3)

Из уравнений (1) и (2) выразим р₁ и р₂ и подставим в уравнение (3):

(4)

С другой стороны, уравнение Менделеева - Клайперона для смеси газов имеет вид:

(5)

Сравнивая (4) и (5) найдем молярную массу смеси газов по формуле:

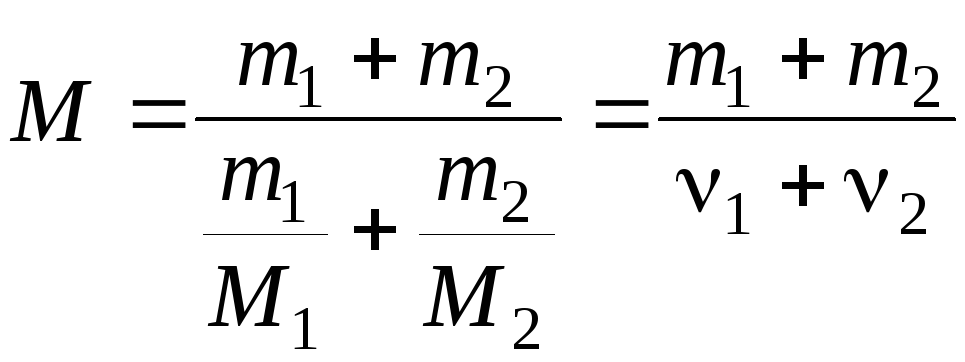, (6)

где ν₁ и ν₂ – число молей гелия и водорода соответственно.

(кг/моль).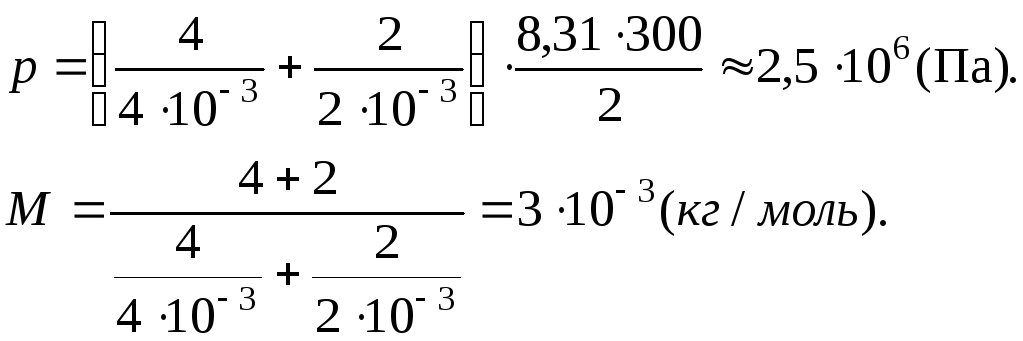

Ответ: 3·10^-3 кг/моль.

Задача 3. При каком давлении средняя длина свободного пробега молекул водорода <λ> = 2,5 см при температуре 68°С? Диаметр молекул водорода принять равным d = 2,3·10 ^–10 м.

Дано: <λ>= 2,5·10-2 м Т= 341 К d= 2,3·10-10 м NA = 6,02·1026 кмоль-1	Решение: Давление водорода при температуре Т можно найти по уравнению Менделеева- Клайперона, в котором удобно ввести число молекул n0 в 1 м3.
р – ?

Это проводится следующим образом:

; ; ;

где N_A – число Авогадро и k – постоянная Больцмана.

Следовательно, Так как, имеем.

Число молекул в 1 м³ выразим через среднюю длину свободного пробега. Из формулы , находим 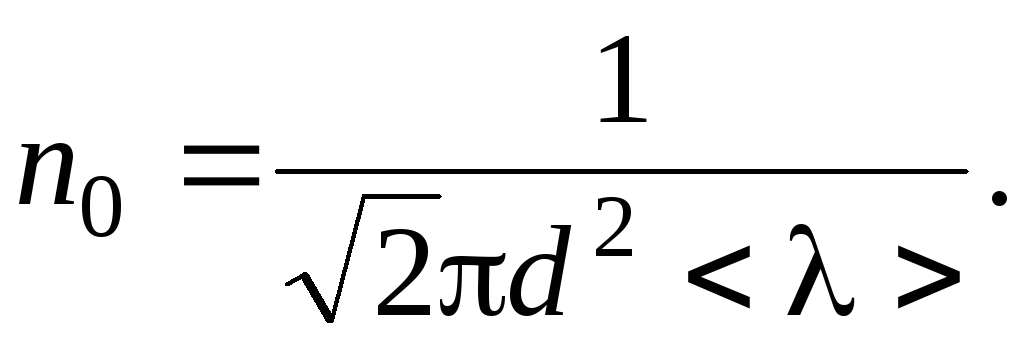Таким образом:

(Па).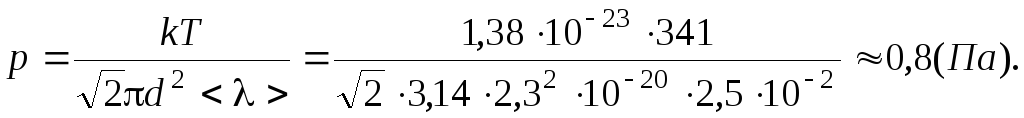

Ответ: 0,8 Па.

Задача 4. Определить плотность разреженного азота, если средняя длина свободного пробега молекул 10 см. Какова концентрация молекул?

Дано: < λ > = 10 см = 0,1 м	Решение: Средняя длина пробега молекулы определяется формулой:
р - ? n0 - ?

, (1)

где d – эффективный диаметр молекул (для азота d = 0,31·10 ^–9 м).

Концентрацию молекул найдем из равенства:

, (2)

где N_A – число Авогадро; М = 28·10 ^–3 кг/моль – молярная масса азота.

Решая совместно уравнения (1) и (2), находим: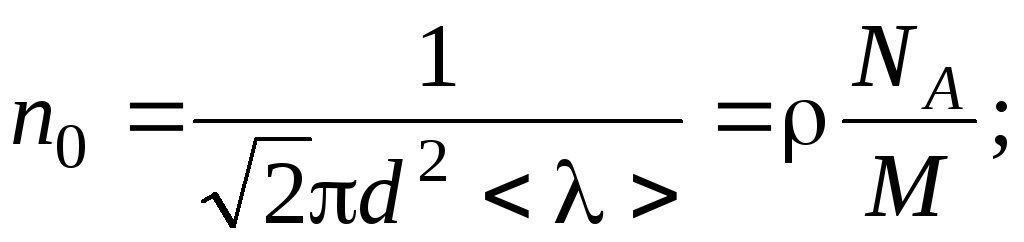

(кг/м³).

Ответ: 1,09·10^-6 кг/м³.

Задача 5. Вычислить коэффициент внутреннего трения и коэффициент диффузии кислорода, находящегося при давлении 0,2 МПа и температуре 280 К.

Дано: p = 2·105 Па d = 2,9·10-10 м М = 32·10-3 кг/моль Т = 280 К	Решение: На основании представлений молекулярно – кинетической теории газов коэффициент внутреннего трения идеального газа (динамическая вязкость) и коэффициент диффузии определяются по формулам:
η - ? D - ?

(1); (2),

где ρ – плотность газа; < λ > – средняя длина свободного пробега молекул; <υ_ар> – средняя арифметическая скорость молекул.

Из (1) и (2) следует (3)

Среднюю арифметическую скорость и среднюю длину свободного пробега молекул находим по формулам:

(4) , (5)

где R = 8,31 Дж/(моль·К) – молярная газовая постоянная; Т – термодинамическая температура; d = 2,9·10 ^–10 м – эффективный диаметр молекулы кислорода; n₀ – число молекул в 1 м³ (концентрация).

Из уравнения Менделеева - Клайперона определяем n₀

(см. задачу 3): (6)

где р – давление; k = 1,38·10 ^–23 Дж/К – постоянная Больцмана.

Подставляя (6) в уравнение (5), получаем:. (7)

Окончательный вид расчетной формулы для коэффициента диффузии найдем, подставляя выражения (4) и (7) в уравнение (2):

. (8)

Плотность кислорода определяется по формуле:. С учетом (6) имеем:. (9)

Подставляя (9) и (8) в (3), получаем расчетную формулу для коэффициента внутреннего трения: .

Вычисляем:

Ответ: .

Задача 6. Наружная поверхность кирпичной стены площадью 25 м² и толщиной 37 см имеет температуру 259 К, а внутренняя поверхность–293 К. Помещение отапливается электроплитой. Определить ее мощность, если температура в помещении поддерживается постоянной. Теплопроводность кирпича 0,4 Вт/(м·К).

Дано: S = 25 м2 D = 37 см = 0,37 м T1 = 259 K T2 = 293R χ = 0,4 Вт/(м·К)	Решение: Количество теплоты, прошедшее через наружную стену, определим по закону Фурье: (1) где t – время протекания теплоты.
N - ?

За время t – электроплита должна выделить такое же количество теплоты: (2)

Приравнивая правые части уравнений (1) и (2), получаем:

,

откуда ,

Ответ: 0,92 кВт.