28. Общее уравнение плоскости в пространстве и его частные случаи. Нормальный вектор плоскости. Условия параллельности и перпендикулярности двух плоскостей.

Определение 1.Уравнение с тремя переменными Ax + By + Cz + D = 0, где A, B и C не равны 0 одновременно, называется общим уравнением плоскости.

Основные виды уравнений плоскости в трехмерном пространстве:

1) z = 0 - уравнение плоскости Oxy;

2) y = 0 - уравнение плоскости Oxz;

3) x = 0 - уравнение плоскости Oyz;

4) Cz + D = 0 - уравнение плоскости, параллельной плоскости Oxy;

5) By + D = 0 - уравнение плоскости, параллельной плоскости Oxz;

6) Ax + D = 0 - уравнение плоскости, параллельной плоскости Oyz;

7) Ax + By + D = 0 - уравнение плоскости, параллельной оси координат Ox;

8) Ax + Cz + D = 0 - уравнение плоскости, параллельной оси координат Oy;

9) Ax + By + D = 0 - уравнение плоскости, параллельной оси координат Oz;

10) Ax + By + Cz = 0 - уравнение плоскости, проходящей через начало координат.

Теорема 1.Любая плоскость в трехмерном пространстве может быть задана общим уравнением.

Определение 2. Вектор (A, B, C) называется общим нормальным вектором плоскости Ax + By + Cz + D = 0.

Если две плоскости заданы общими уравнениями A₁x + B₁y + C₁z + D₁ = 0и A₂x + B₂y + C₂z + D₂ = 0, то:

- плоскости параллельны тогда и только тогда, когда их нормальные векторы коллинеарны:   ;

- плоскости перпендикулярны тогда и только тогда, когда скалярное произведение их нормальных векторов равно нулю: A₁A₂ + B₁B₂ + C₁C₂ = 0.

A(x-x₀) + B(y-y₀) + C(z-z₀) = 0 - уравнение прямой, проходящей через точку (x₀, y₀, z₀), перпендикулярно нормальному вектору.

29. Уравнения прямой линии в пространстве как линии пересечения двух плоскостей. Канонические уравнения прямой. Направляющий вектор прямой. Условия параллельности и перпендикулярности двух прямых в пространстве.

Уравнения прямой линии в пространстве как линии пересечения двух плоскостей. Канонические уравнения прямой. Направляющий вектор прямой. Условия параллельности и перпендикулярности двух прямых в пространстве

Существует несколько способов задания прямой в трехмерном пространстве:

1) 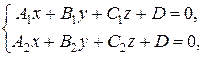  - прямая как линия пересечения двух плоскостей задается аналитически системой двух линейных уравнений;

2)   - канонические уравнения прямой, где (m, n, p) – направляющий вектор прямой (т.е. прямая параллельна этому вектору), M₁(x₁, y₁, z₁) – некоторая точка, лежащая на данной прямой.

Если две прямые заданы каноническими уравнениями 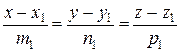  и   , то:

- прямые параллельны тогда и только тогда, когда их направляющие векторы коллинеарны:   ;

- прямые перпендикулярны тогда и только тогда, когда скалярное произведение их направляющих векторов равно нулю: m₁m₂ + n₁n₂ + p₁p₂ = 0;

Если две плоскости заданы общими уравнениями A₁x + B₁y + C₁z + D₁ = 0и A₂x + B₂y + C₂z + D₂ = 0, то угол j между плоскостями равен углу между нормальными векторами (A₁, B₁, C₁) и (A₂, B₂, C₂), следовательно,

 .

Если две прямые заданы каноническими уравнениями   и   , то угол j между прямыми равен углу между направляющими векторами (m₁, n₁, p₁) и (m₂, n₂, p₂), следовательно,

 .

Если плоскость задана общим уравнением Ax + By + Cz + D = 0, а прямая задана каноническими уравнениями   , то угол j между прямой и плоскостью равен дополнительному углу к углу между нормальным вектором (A, B, C) и направляющим вектором (m, n, p), следовательно,

 .

В последнем случае:

- плоскость и прямая параллельны тогда и только тогда, когда скалярное произведение их нормального и направляющего векторов равно нулю:

Am + Bn + Cp = 0.

- плоскость и прямая перпендикулярны тогда и только тогда, когда их нормальный и направляющий векторы коллинеарны:

 .