1.6.5. Закон сохранения энергии.

Складывая (1.6.13) и (1.6.16), получаем уравнение, выражающее общий закон сохранения энергии для контрольного объёма сплошной среды (6.6.4):

.

Как следует из полученного соотношения, работа внутренних сил не изменяет полную энергию системы жидких частиц: она уменьшает механическую энергию и увеличивает тепловую. Что является выражением второго закона термодинамики.

Для перехода к Эйлерову неподвижному объему используется теорема о дифференцировании по времени функции, как интеграла по подвижному объему (1.4.10).

, (1.4.10)

Окончательно для неподвижного контрольного объема законы сохранения примут вид:

Закон сохранения массы:

, (1.6.17)

Закон сохранения импульса:

, (1.6.18)

Закон сохранения энергии:

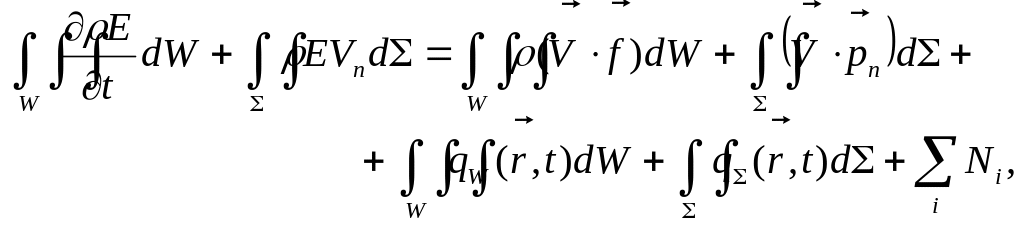(1.6.19)

. (1.6.20)

где: - удельная полная энергия среды.

1.8. Система дифференциальных уравнений гидромеханики.

В случае, если параметры потока не терпят разрыва, и могут быть описаны функциями непрерывными со своими производными, удобно использовать законы сохранения в виде дифференциальных уравнений в частных производных. Для перехода к такой форме записи от интегральной, используют теорему Остроградского – Гаусса (1.4.7). Подобный подход был подробно рассмотрен при выводе уравнения неразрывности:

. (1.4.13)

Привлекая формулы Коши (1.5.3) и применяя теорему Остроградского – Гаусса получим:

.

Подставляя их в интегральную форму записи закона сохранения импульса (1.6.18) имеем:

, (1.6.21)

Учитывая, что объем – произволен, получим векторное уравнение в частных производных – дифференциальную форму записи закона сохранения импульса, которую принято называть уравнениями движения сплошной среды в напряжениях:

, (1.6.22)

расписывая по координатам:

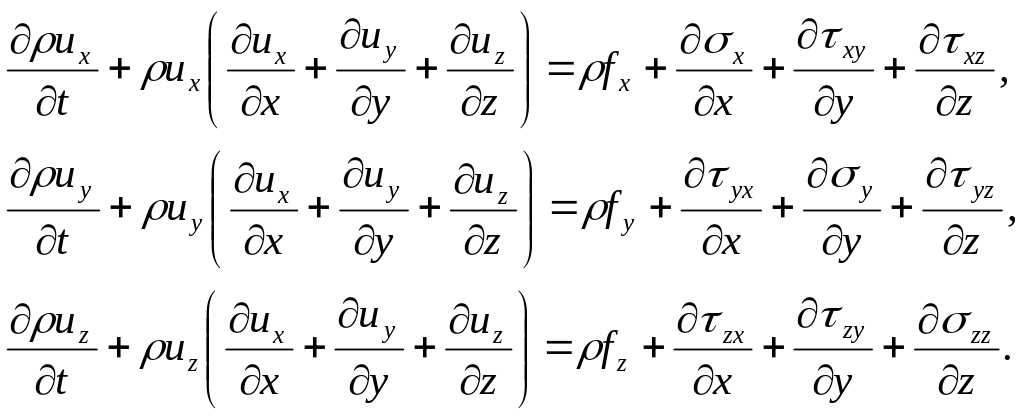(1.6.23)

Компоненты тензора напряжений для случая ньтоновской жидкости (1.5.23):

(1.6.24)

Подставляя (1.6.24) в (1.6.23) и используя уравнение неразрывности (1.4.13), получим систему уравнений движения для вязкой сжимаемой жидкости, которая носит название системы уравнений Навье-Стокса:

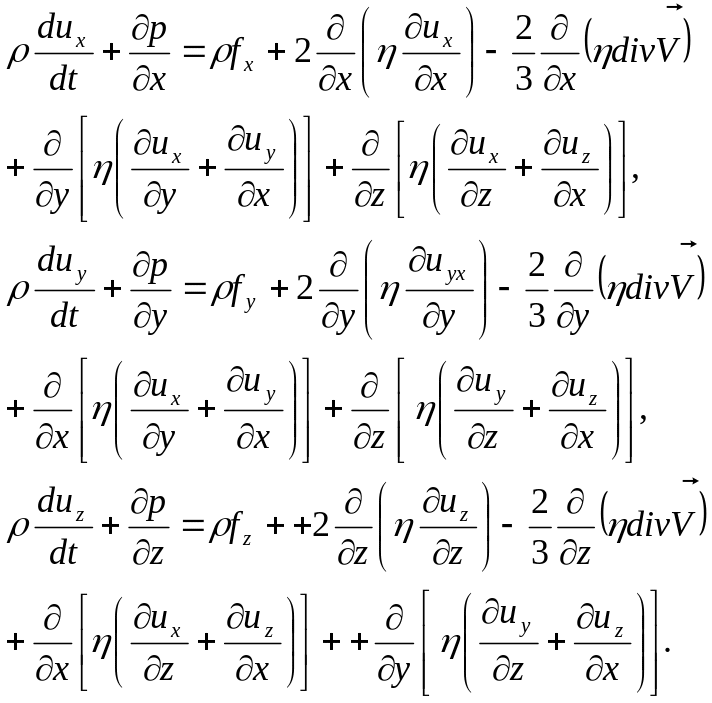(1.6.25)

Повторяя процедуру перехода к интегралу по объему для закона сохранения энергии имеем:

, ,

Используя эти соотношения, получим еще одну форму записи закона сохранения энергии:

Для перехода к дифференциальной форме записи, необходимо ввести понятие вектора теплового потока:

, (1.6.26)

где - коэффициент теплопроводности, ; - абсолютная температура. Знак минус показывает, что тепло передается от более нагретого тела к менее нагретому.

Соответственно:

,

,

(1.6.27)

Или в дифференциальной форме без учета устройств, изменяющих механическую энергию потока, уравнение энергии для вязкой теплопроводной сплошной среды:

. (1.6.28)

В итоге, для описания движения вязкой сплошной сжимаемой среды может быть использована система дифференциальных уравнений в частных производных, состоящая из уравнения неразрывности (1.4.13), уравнений Навье-Стокса (1.6.25), уравнения энергии (1.6.28) и уравнения состояния среды.

Для несжимаемой среды система имеет более простой вид. Уравнение неразрывности переходит в уравнение несжимаемости (1.4.4), уравнения Навье-Стокса и энергии существенно упрощаются, уравнение состояния становится не нужным:

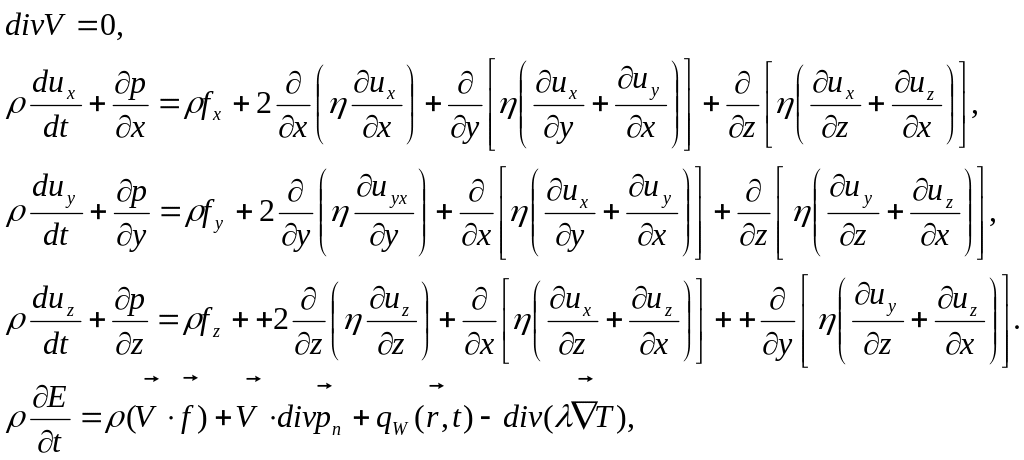(1.6.29)