3.2. Уравнение Бернулли для установившегося напорного потока вязкой жидкости

Рассмотрим установившееся движение в трубопроводе, для которого справедливы предположения об одномерности течения. Для этого выделим в трубопрово­де (рис. 3.2) сечениями 11 и 22, в которых движение равномерное, контрольный объем , ограниченный контрольной поверхностью , которая показана на рисунке штриховой линией. Запишем для выделен­ного объема закон изменения кинетической энергии (1.6.20):

. (3.2.1)

Рис.3.2. К выводу уравнения Бернулли для одномерных напорных потоков

Первое слагаемое равно нулю, так как движение жидкости установивше­еся . Второе слагаемое - второе слагаемое представляет собой поток кинетической энергии через контрольную поверхность . Следовательно:

Рассмотрим граничные условия на , учитывая одномерность потока во входном и выходном сечениях:

(3.2.2)

Тогда:

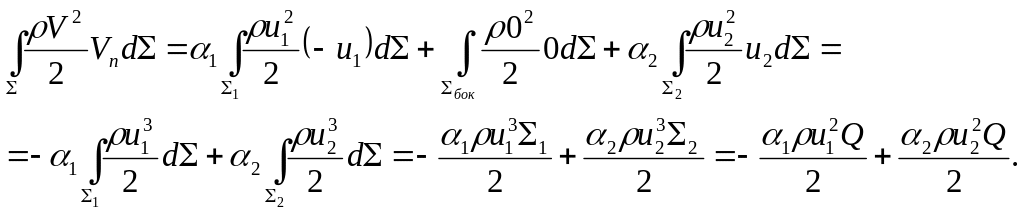
Здесь - объемный расход, а величина носит название коэффициента Кориолиса, физический смысл которого будет показан ниже.

Рассмотрим далее члены в правой части уравнения (3.2.1), начнем со слагаемого, выражающего мощность внешней массовой силы. Предположим, что внешняя массовая сила имеет потенциал, т.е. существует такая скалярная функция , для кото­рой . Ограничимся случаем, когда сила тяжести является единственной внешней массовой силой . Используя теорему Остроградского  Гаусса и граничные условия (3.2.2), получим:

. (3.2.3)

Полученное равенство позволяет выразить мощность внешней мас­совой силы через поток потенциальной энергии, обусловленной этой силой, сквозь живые сечения.

Второй интеграл, выражающий мощность внешней поверхно­стной силы:

. (3.2.4)

В сечении 1  1 скорость имеет только нормальную составляющую , так как движение здесь равномерное или плавноизменяющееся. Чтобы вы­числить скалярное произведение , зададим в произвольной точке живого сечения систему ортогональных координат (рис. 3.2), определяе­мую тремя единичными векторами , из которых  нормален к живому сечению, a и лежат в плоскости живого сечения. Проектируя на эти коор­динатные оси векторы u и р_n, находим:

,

Аналогичные вычисления выполним для живого сечения . На поверхности выполняется условие прилипания. Согласно полученным результатам, а также используя (3.2.2), на контрольной поверхности имеем условия:

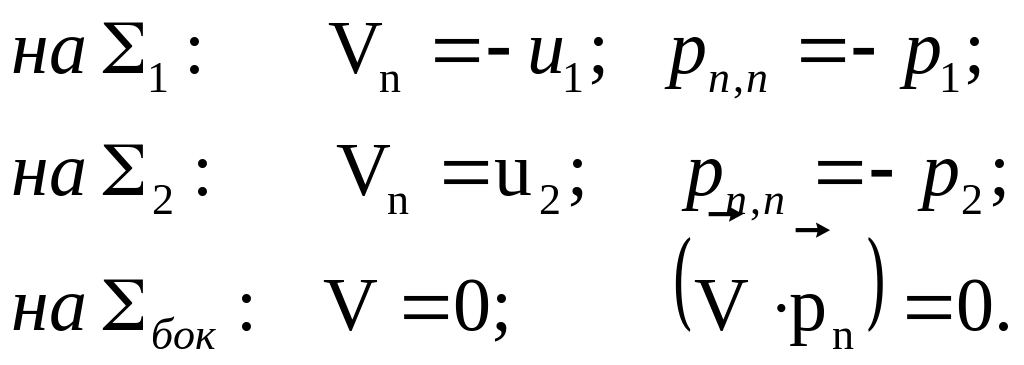(3.2.5)

Подставляя (3.2.5) в (3.2.4), получаем:

. (3.2.6)

Согласно равенству (3.2.6) мощность внешней поверхностной силы можно интерпретировать как поток, обусловленный этой силой потен­циальной энергии потока сквозь живое сечение; плот­ность распределения этой энергии равна давлению р.

Последнее слагаемое в (3.2.1), выражающее мощность внутренних сил в пределах контрольного объема (диссипацию энергии), оставляем без преобразования.

Подставив полученные выражения, в исходное уравнение (3.2.1) и разделив все слагаемые на весовой расход , получим искомое уравнение Бернулли:

, (3.2.7)

где  = g удельный вес, а слагаемое

, (3.2.8)

выражает отнесенную к весовому расходу мощность внутренних сил (дис­сипацию механической энергии в единицу времени) в пределах конт­рольного объема.

Если используется модель идеальной жидкости (трение между слоями жидкости отсутствует ), то уравнение Бернулли принимает вид:

В этом случае имеет место закон Бернулли, который гласит: При установившемся движении несжимаемой идеальной жидкости сумма геометрической, скоростной и пьезометрической высот вдоль линии тока остаётся постоянной.