101

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ИНСТИТУТ ПРИРОДНЫХ РЕСУРСОВ

КАФЕДРА ХРАНЕНИЯ И ТРАСПОРТИРОВКИ НЕФТИ И ГАЗА

Цимбалюк Александр Федорович

8-905-990-10-80

afctgu@yandex.гu

Гидравлика и нефтегазовая гидромеханика

Оглавление

Аннотация 3

1.Введение. Основы механики сплошной среды. 6

1.3. Физические свойства жидкостей, газов и твердых тел. 9

Молeкулярная масса – (ранее молекулярный вес) безразмерная величина равная средней массы молекулы природной смеси изотопов вещества к 1/12 массы атома изотопа ¹²С. 14

Массовое число – общее число нуклонов (протонов и нейтронов) в атомном ядре. Массовое число указывается слева вверху символа изотопа. ²³⁵U 14

1.5. Силы и напряжения в сплошной среде. Тензор напряжений. Деформации в сплошной среде. Тензор деформаций. Тензор скоростей деформаций. 24

1.6. Законы сохранения. 30

1.6.1. Закон сохранения импульса. 31

1.6.2. Закон сохранения момента количества движения. 31

1.6.3. Закон изменения кинетической энергии. 32

1.6.4. Закон изменения внутренней энергии. 34

1.6.5. Закон сохранения энергии. 34

1.8. Система дифференциальных уравнений гидромеханики. 35

1.9. Основы теории размерностей и подобия. - теорема. Подобие физических явлений, моделирование. 37

2.Гидростатика. 40

2.1. Равновесие жидкости. Уравнение равновесия. 40

2.2. Абсолютное, избыточное давление. Вакуум. 42

2.3. Сила давления жидкости на плоскую поверхность. Центр давления. Гидростатический парадокс. Давление жидкости на криволинейные поверхности. 44

2.4. Приборы для измерения давления. 48

2.5. Условия плавания тел. Закон Архимеда. 50

3. Гидромеханика. 51

3.1. Одномерные установившиеся течения вязкой жидкости. Основные понятия. 51

3.2. Уравнение Бернулли для установившегося напорного потока вязкой жидкости 53

3.3. Геометрическая и энергетическая интерпретация уравнения Бернулли. 55

3.4. Потенциальный и полный гидродинамические напоры. Пьезометрическая линия. 56

3.5. Течение жидкости в круглых трубах. 59

3.6. Безнапорные потоки. Струи. 66

3.7. Гидравлический удар в трубах. Формула Жуковского. 68

3.8. Уравнение Бернулли для газа. Одномерное течение газа. Критические параметры. Сопло Лаваля. 69

4. Основы реологии. 71

4.1. Реологические модели жидкостей. 71

4.2. Моделирование движения сложных сред 74

4.2.2. Неньютоновские жидкости. 75

4.2.3.Механические модели неньютоновских сред 76

5. Движение жидкостей и газов в пористой среде. 79

5.1.Основные понятия. 79

5.2.Определение эффективного диаметра. 83

5.3.Формулы фильтрации. 84

6.Кавитация. 86

6.Гетерогенные потоки. 86

6.1. Коэффициенты сопротивления и теплообмена частиц. 87

6.2. Основные уравнения для двухфазных монодисперсных течений 90

6.3. Система уравнений для полидисперсного течения 93

6.4. Равновесное и замороженное двухфазные течения 94

Приложение 1. Краткие сведения из математики. 96

Приложение.2 Программа Long_01 для расчета характеристик длинных трубопроводов. 99

Аннотация

Учебное пособие содержит основные сведения из курса гидравлики, адаптированного к течениям жидких и газообразных углеводородов. В частности особое внимание уделено расчету сложных и простых трубопроводов, неньютоновским жидкостям и основам фильтрации. Пособие используется при чтении лекций по курсу «Гидравлика. Нефтегазовая гидромеханика» на втором курсе ИПР ТПУ. Курс лекций дополнен сборником задач.

Список рекомендованной литературы:

1. Гусев А.А. Гидравлика: учебник для вузов. –М.: Изд-во Юрайт, 2013. -285с.

2. Гусев В.П., Гусева Ж.А. Основы гидравлики. Учебное пособие. Томск: Изд-во Томского политехнического университета, 2012.— 222 с.

3. Басниев К.С., Дмитриев Н.М., Розенберг Г.Д. Нефтегазовая гидромеханика.- М.- Ижевск: ИКС,2005.-544с.

4. Лурье М.В. Задачник по трубопроводному транспорту нефти, нефтепродуктов и газа: Учеб. пособие для вузов. – М.: ООО "Недра-Бизнесцентр", 2003. – 349 с.

5. Шестаков В.М. Гидрогеомеханика. Учеб. пособие для вузов. –М.: Изд-во МГУ, 1998. – 72с.

Основные обозначения.

- координаты точки в декартовой прямоугольной системе координат;

- радиус вектор точки;

- время, ; - температура в градусах Цельсия, ;

- плотность, ;

- газовая постоянная ;

- гидравлический радиус ;

- число Рейнольдса;

 = g - удельный вес, ;

- показатель адиабаты газа;

- абсолютная температура, ;

- вектор скорости, ;

- коэффициент динамический вязкости, ;

- коэффициент кинематический вязкости, ;

- коэффициент Пуассона;

- коэффициент теплопроводности, ;

- коэффициент гидравлического трения;

- модуль объемной упругости;

- объем Лагранжа, и окружающая его замкнутая поверхность;

- объем Эйлера, и окружающая его замкнутая поверхность;

- диссипативная функция;

- удельная внутренняя энергия;

- удельная полная энергия среды;

- радиус трубы;

- смоченный периметр;

- тензор напряжений;

- тензор деформаций;

- тензор скоростей деформаций;

- объемный расход;

- поток массы;

- поток кинетической энергии;

- весовой расход;

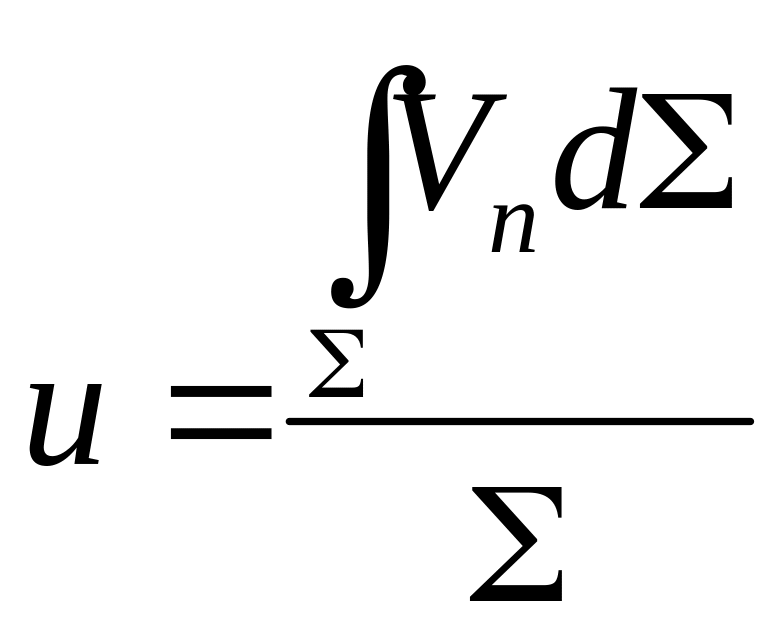- средняя скорость в живом сечении; 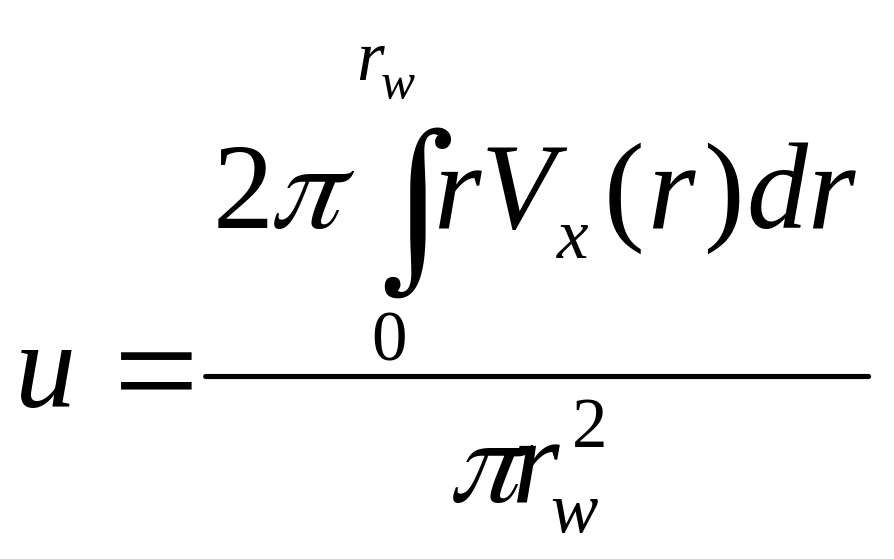- средняя скорость в живом сечении круглой трубы;

1.Введение. Основы механики сплошной среды.

1.1. Предмет и метод механики сплошной среды. Гипотезы механики сплошной среды. Свойства Скалярные и векторные поля. Силы и напряжения в сплошной среде. Тензор напряжений. Законы сохранения.

Механика сплошных сред (МСС)  раздел механики, в рамках которого исследуются движения и деформации газообразных, жидких и твердых тел.

В МСС полагают, что справедлива гипотеза сплошности: масса не сосредоточена в молекулах и атомах, а непрерывно распределена в пространстве, занятом физическим телом. Это позволяет не учитывать непосредственно детали молекулярной структуры среды, а использовать математическую модель непрерывного континуума¹, и применять аппарат дифференциального и интегрального исчисления. Такая модель называется моделью сплошной среды.

В МСС используется понятие геометрического пространства, обычно используется евклидово пространство, для которого можно ввести единую декартову систему координат, а расстояние между любыми точками М_i и М_j определяется по формуле:

, (1.1.1)

где x_i , y_i , z _i и x _j , y_j , z _j - декартовы координаты точек М_i и М_j .

При решении большинства задач МСС, следуя Ньютону, считается, что время не зависит от системы координат и течет для всех наблюдателей одинаково, независимо от того, где они находятся: дома, в поезде или в самолете. Такое время называется абсолютным.

В том случае, если физические свойства сплошной среды (агрегатное состояние, теплоемкость и др.) одинаковы и не меняются от точки к точке, то среда называется гомогенной. Примерами таких сред могут служить чистые газы и жидкости, однородные кристаллы.

Критерием применимости модели сплошной среды является неравенство – условие сплошности среды:

, (1.1.2)

где l – характерный микроразмер (для газа - длина свободного пробега молекул, для кристалла – размер ячейки кристаллической решетки); L – характерный макроразмер задачи (диаметр трубы или размер тела, обтекаемого потоком газа или жидкости).

Многофазной, или гетерогенной, средой называется среда с разнородными включениями. В частности, к гетерогенным средам относятся пористые тела (роль включений играют поры, заполненные газом или жидкостью), газовзвеси (механические смеси газов с твердыми или жидкими частицами), эмульсии (смеси жидкостей с каплями других жидкостей) и др. В отличие от гомогенных сред условия сплошности для гетерогенных сред имеют вид:

, (1.1.3)

где а – характерный размер включения (например, радиус частицы пыли).

Фазой называется термодинамически однородная по свойствам часть термодинамической системы, отделенная от других фаз поверхностями раздела, на которых скачком изменяются некоторые свойства системы. В однокомпонентной системе разные фазы могут быть представлены различными агрегатными состояниями или разными полиморфными модификациями вещества. В многокомпонентной системе фазы могут иметь различный состав и структуру.

Таким образом, в МСС исследуются макроскопические процессы в окружающем нас мире.

Помимо обычных материальных тел в МСС рассматриваются также особые среды – физические поля: гравитационные и электромагнитные, в том числе и поле излучения.

Обобщая сказанное, можно сформулировать основные гипотезы механики сплошной среды: