Випадкові величини

Приклад.

Закон розподілу випадкової величини задається таблицею:

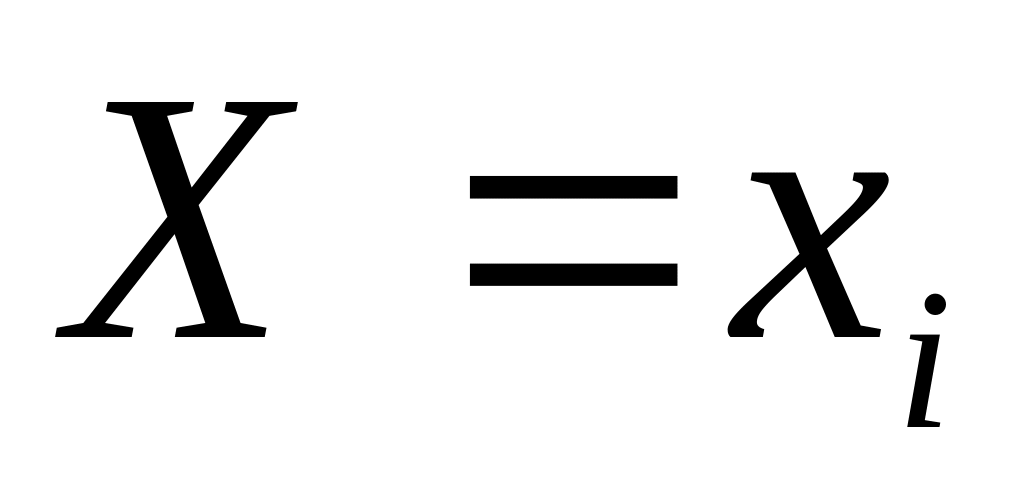
	0	1	2	3	4	5
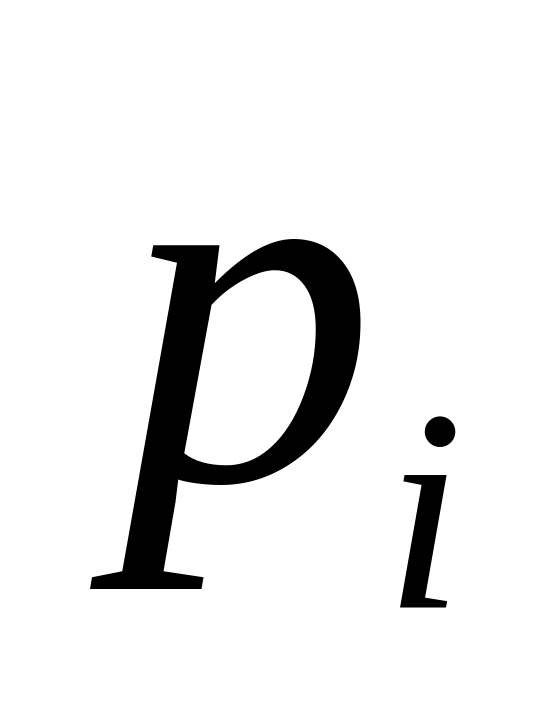
	0,00032	0,0064	0,0512	0,2048	0,4096	0,3277

1) Побудуємо функцію розподілу :

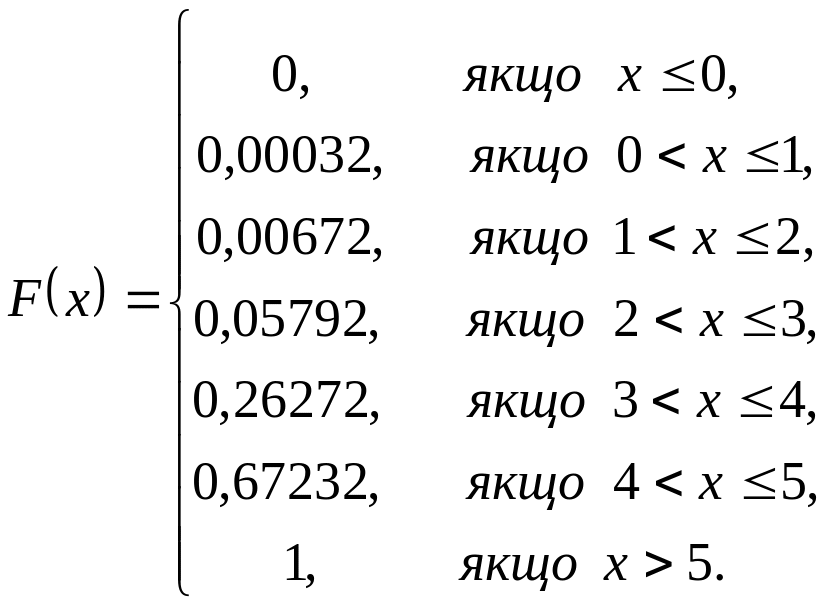
Графік функції

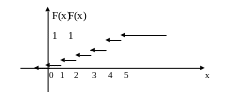
2) Математичне сподівання

Дисперсія

Середнє квадратичне відхилення

3) .

4)

Приклад. Задано функцію розподілу ймовірностей неперервної випадкової величини

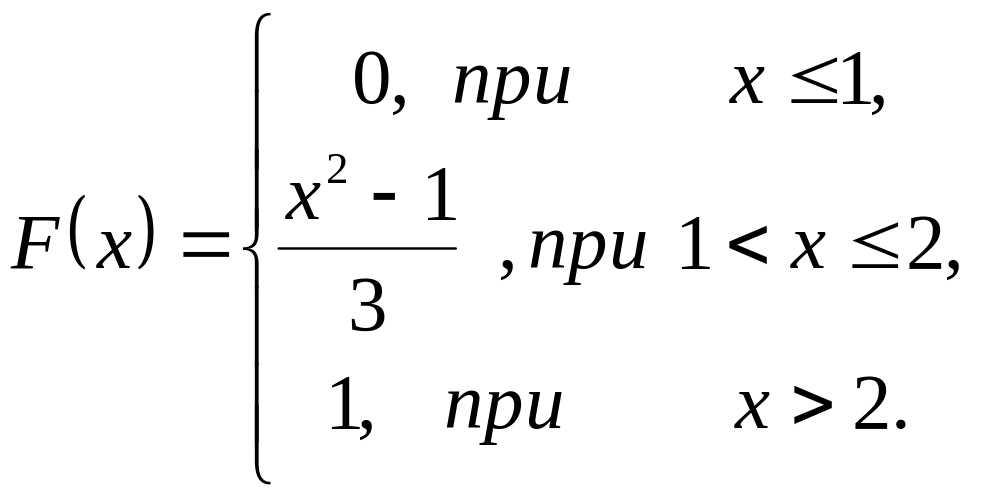
1) Знайти диференціальну функцію (щільність розподілу),

2) Побудувати графіки функції та щільності розподілу.

3) Знайти математичне сподівання , дисперсію , середнє квадратичне відхилення ,

4) Знайти моду та медіану

5) Обчислити ймовірність

Розв’язання. 1) Знайдемо щільність розподілу

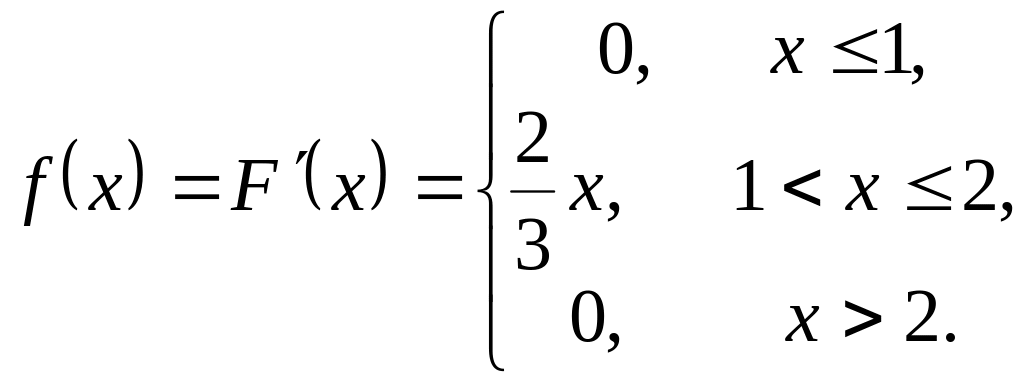
2) Побудуємо графіки функції та щільності розподілу

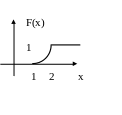
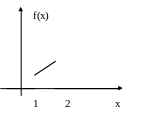
3) Знайдемо математичне сподівання:

Обчислимо дисперсію:

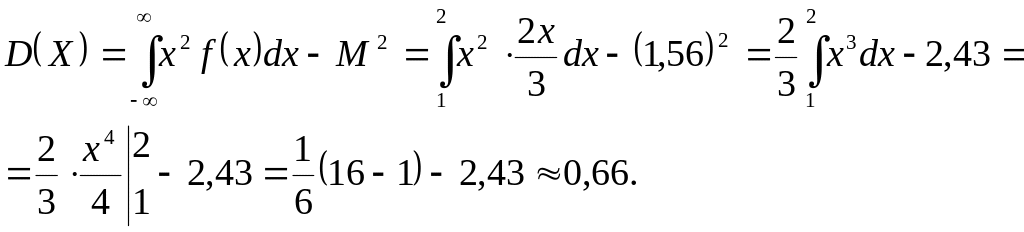
Тепер знайдемо середнє квадратичне відхилення

4) Моду визначимо з умови З графіка щільності випливає, що мода

Медіану визначимо з умови

5) Ймовірність події обчислюється за формулою

Тому

Приклад. Випадкова величина має нормальний закон розподілу з відомим середнім квадратичним відхиленням Знайти довірчий інтервал для оцінки невідомого математичного сподівання за вибірковою середньою якщо об’єм вибірки і задана надійність оцінки

Розв’язання. Довірчі інтервали для оцінки невідомого математичного сподівання визначаються формулою:

.

Знайдемо . Із співвідношення отримаємо В таблиці знаходимо Обчислимо точність оцінки:

Довірчі інтервали будуть такими:

Якщо то довірчий інтервал має такі довірчі межі:

Таким чином, значення невідомого параметра , які узгоджуються з даними вибірки, задовольняють нерівність

Системи випадкових величин

Приклад. Закон розподілу системи двох дискретних випадкових величин заданий таблицею:

Знайти:

1) ;

2) закони розподілу та ;

3) числові характеристики та ;

4) коваріацію , коефіцієнт кореляції ;

5) ;

6)

Розв’язання. 1) За умовою нормування

a тому

,

Звідки

2) Тоді матриця розподілу системи двох випадкових величин набуває вигляду:

				1

3) Обчислимо основні числові характеристики та :

4) Обчислимо коваріацію

Оскільки то між даними величинами існує кореляційний зв’язок. Для вимірювання тісноти кореляційного зв’язку обчислюємо коефіцієнт кореляції

Отже, між даними величинами існує слабка пряма залежність.

5)

6) Для обчислення необхідно побудувати відповідні закони розподілу.

Умовний закон розподілу

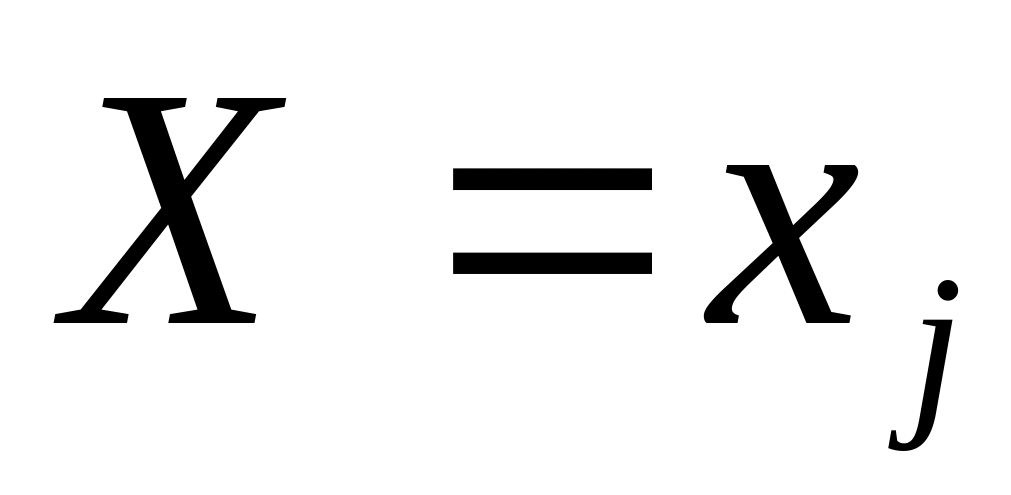
	5,2	10,2	15,2

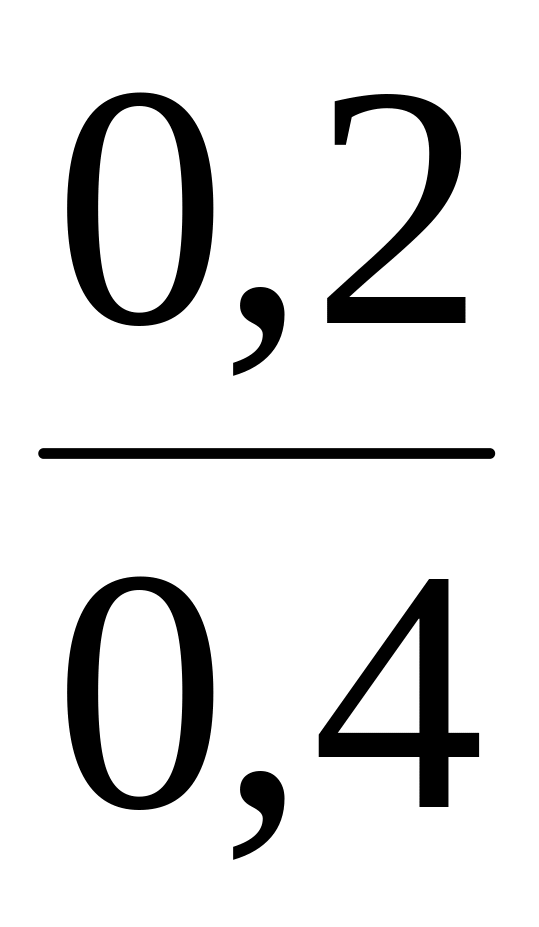
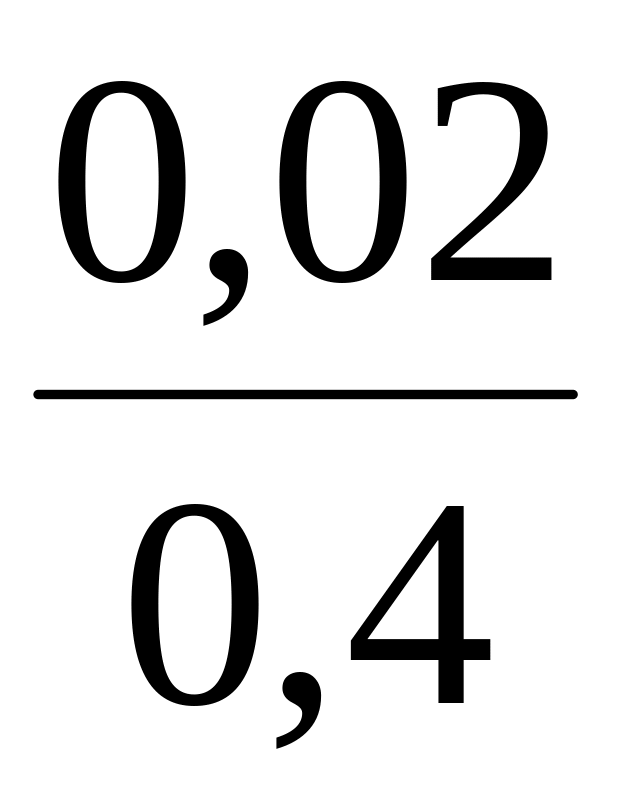
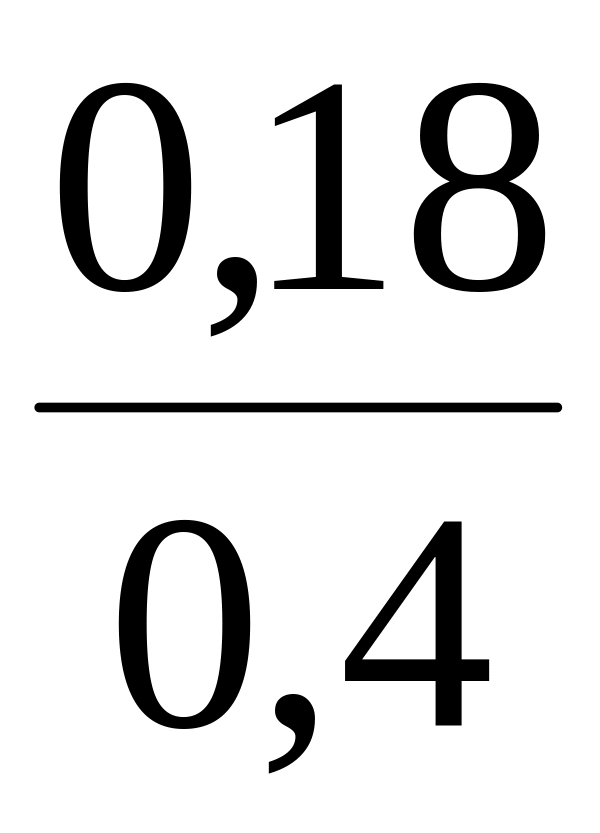
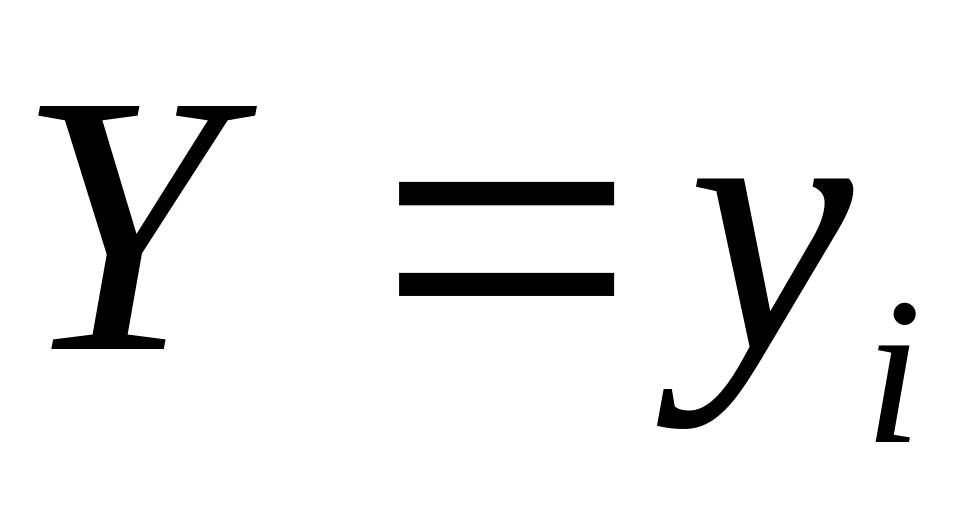
	2,4	4,4	6,4
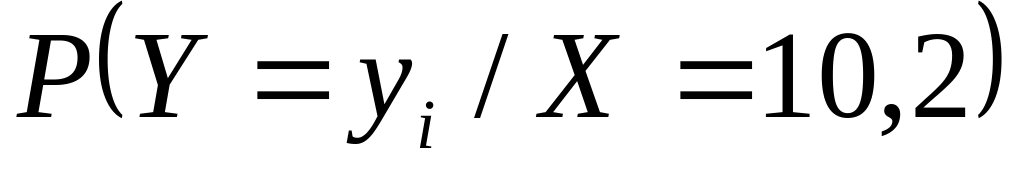
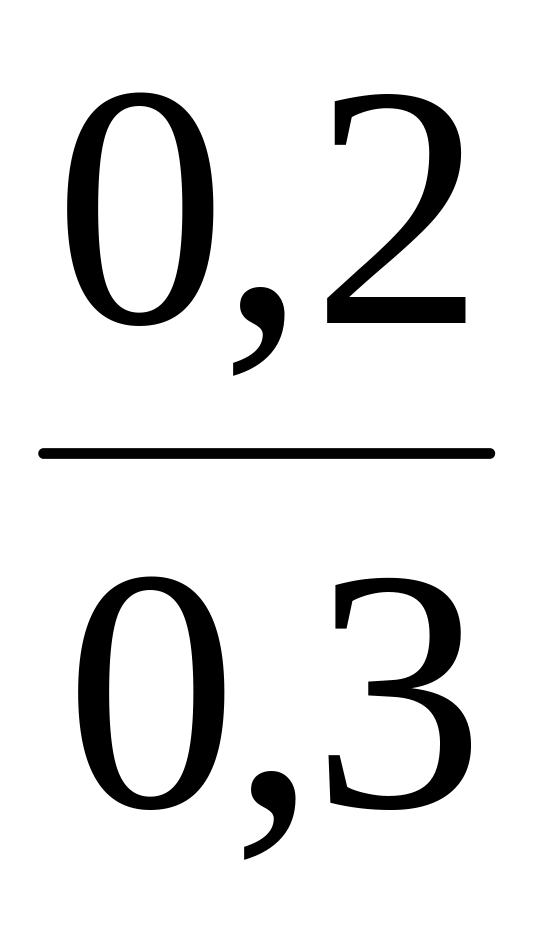
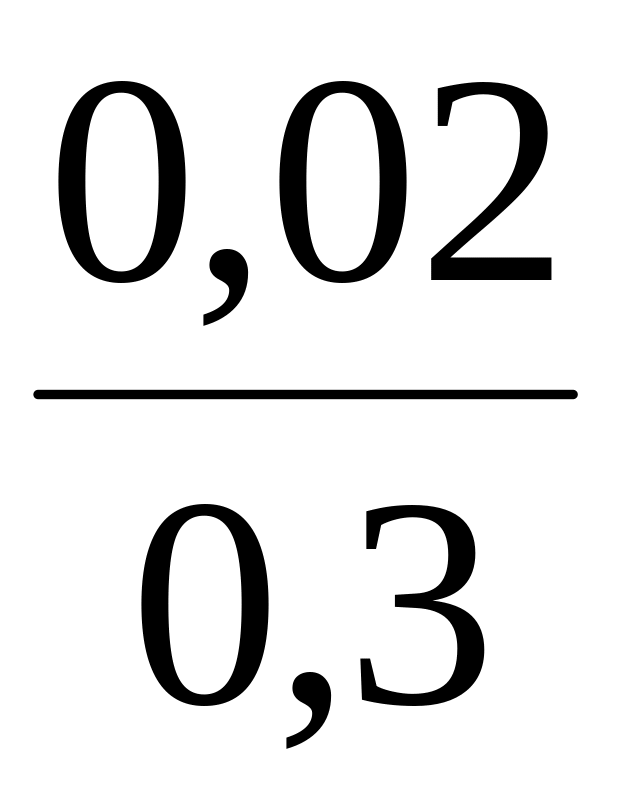
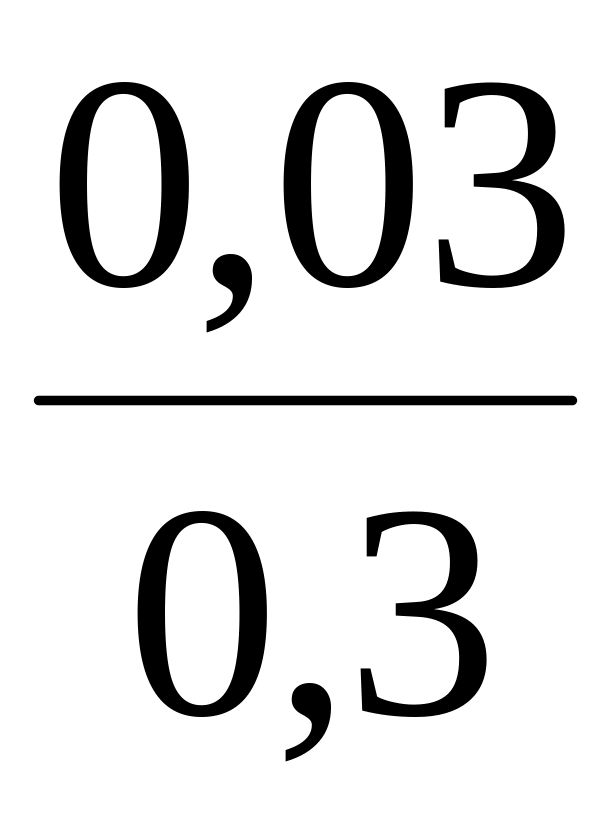