Дискретна математика.

Завдання № 1. Спростити вирази алгебри множин за допомогою властивостей операцій над множинами:

1) ;

2) .

Розв’язання:

1) Властивості 1, 1^*;

Властивість 3^*;

Властивість 8^*;

Властивість 7;

Властивість 2^*;

Властивість 8^*;

.

2) Властивість 2^*;

Властивість 3^*;

Властивість 8^*;

Властивість 3^*;

Властивість 8;

Властивість 7^*;

Властивість 8;

.

Завдання № 2. Розв’язати задачі:

1. В розіграші першості по футболу беруть участь 16 команд, при цьому будь-які дві з них грають між собою тільки один матч. Скільки всього календарних ігор?

Розв’язання. .

1′. В групі 30 студентів. Кожен з них потиснув руку всім іншим. Скільки зроблено рукостискань?

Розв’язання. .

1′′. У поштовій скриньці 38 відділень. Скількома способами можна покласти в скриньку 35 однакових листів таким чином, щоб в кожному відділенні було б не більше одного листа?

Розв’язання.

.

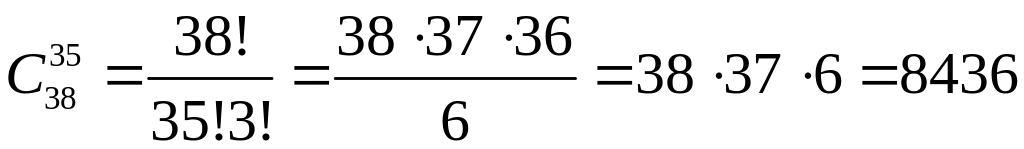1′′′. Скількома способами можна розмістити трьох коней по чотирьох стійлах?

Розв’язання. .

2. 1) Скільки 2-значних різних чисел можна скласти з цифр 1, 2, 3 ?

2) Скільки 3-значних різних парних чисел можна скласти з цифр 1, 2, 3, 4?

3) Скільки 3-значних різних парних чисел можна скласти з цифр 0, 1, 2, 3, 4?

Розв’язання.

1) .

2) .

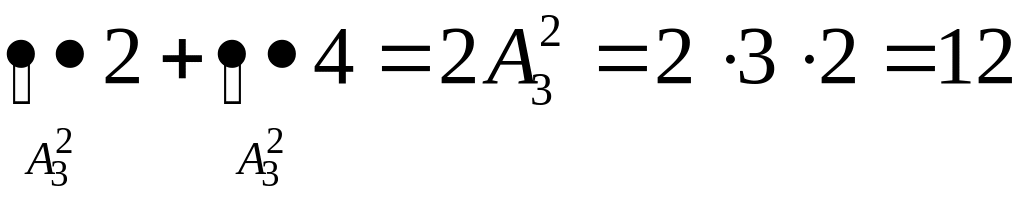3)

.

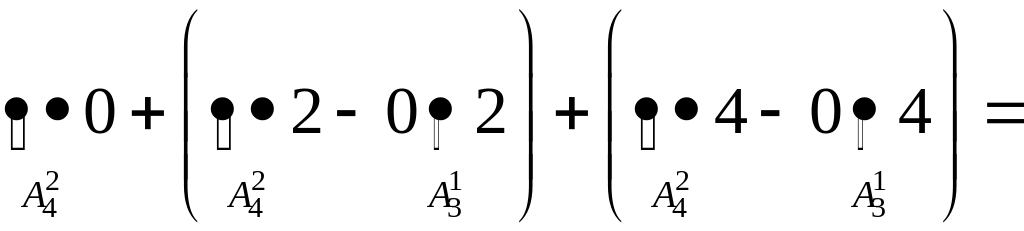
3. 1) Скільки перестановок можна скласти з цифр 0, 1, 2, 3,4 ?

2) Скільки 5-значних різних чисел можна скласти з цифр 0, 1, 2, 3, 4?

3) Скільки парних 5-значних різних чисел можна скласти з цифр 0, 1, 2, 3, 4?

Розв’язання.

1) ;

2) ;

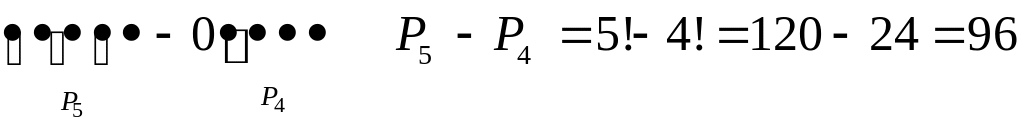3) ,

.

3′. Між перестановками цифр числа 12345 скільки таких, які починаються:

1) цифрою 1; 2) числом 12; 3) числом 123?

Розв’язання.

1) ;

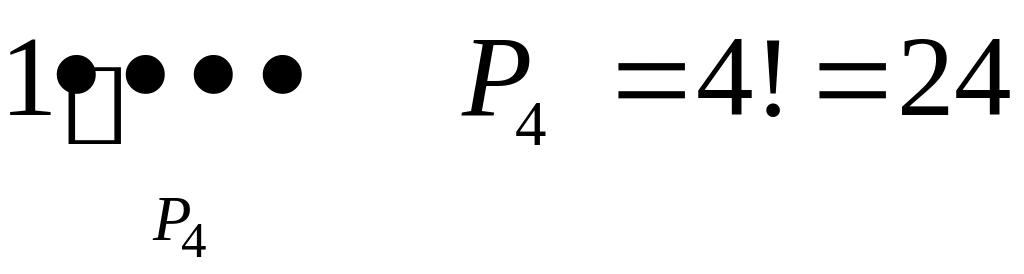2) ;

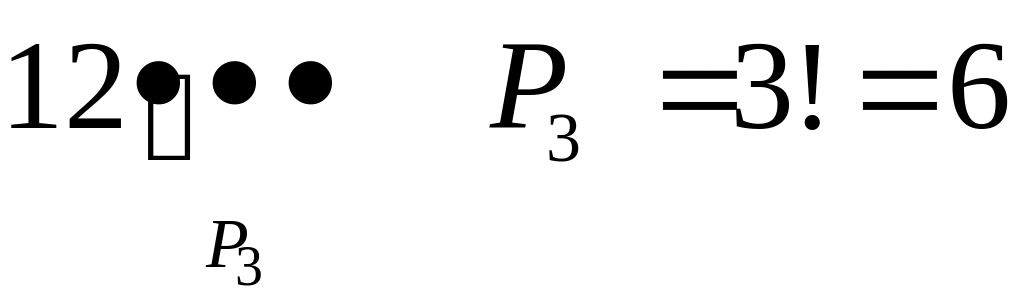3)

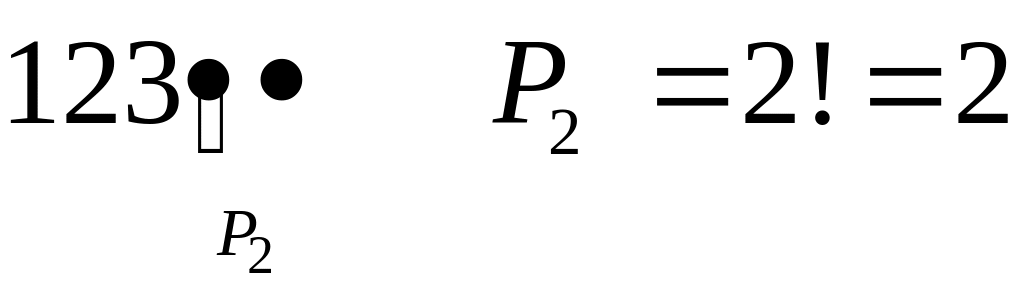
4. 1) Скільки існує 7-значних телефонних номерів, в кожному з яких жодна цифра не повторюється?

2) Скільки існує 7-значних телефонних номерів, які не містять інших цифр, крім 2,3,5 і 7?

Розв’язання. 1) Задача про число розміщень по семи різним місцям семи з десяти різних цифр:

.

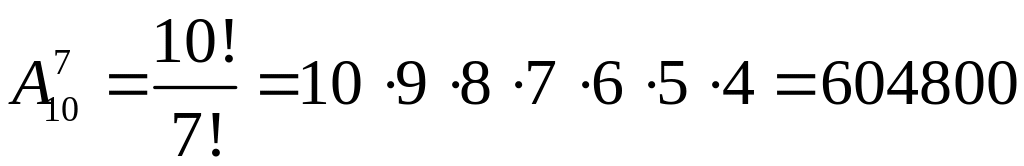2) Задача про число розміщень по семи різним місцям семи цифр, які вибираються з чотирьох різних цифр з повтореннями кожної з них будь-яке число разів, але не більше семи.

.

5. Скількома способами можна розподілити 10 осіб на 3 групи відповідно по 2, 3, 5 осіб в групі?

Розв’язання.

.

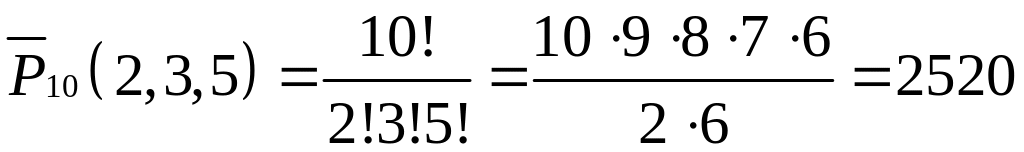6. Скількома способами можна вибрати чотири монети з чотирьох п’ятикопійкових і з чотирьох двохкопійкових?

Розв’язання. 2,2,2,2, 5,5,5,5

.

7. Скількома способами можна скласти наряд з трьох солдатів і одного офіцеру, якщо є 50 солдатів і 3 офіцера?

Розв’язання.

.

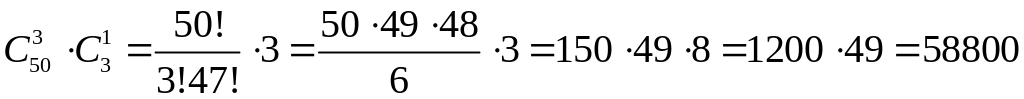8. З двох юристів і 10 економістів треба утворити комісію у складі 8-ми осіб. Скількома способами можна утворити комісію, якщо до її складу повинен входити хоча б один юрист?

Розв’язання.

.

9. Із цифр 1,2,3,4,5,6,7,8,9 утворюються різні п’ятизначні числа, що не мають однакових цифр. Визначити кількість чисел, в яких одночасно є цифри 2,4 і 5.

Розв’язання.

Завдання № 3. Для заданої булевої функції:

1) скласти таблицю істинності;

2) знайти ДДНФ і ДКНФ двома способами:

а) за допомогою таблиці ісинності,

б) за допомогою рівносильних перетворень.

3) знайти зображення у вигляді многочлена Жегалкіна.

4) з’ясувати належність до функціонально замкнених класів.

1) ;

1)' .

Розв’язання.

1) .

1) Побудуємо таблицю істинності даної булевої функції:

0	0	0	1	0	0	1
0	0	1	1	0	0	1
0	1	0	1	1	0	0
0	1	1	1	1	0	0
1	0	0	0	0	0	1
1	0	1	0	0	1	1
1	1	0	1	1	0	0
1	1	1	1	1	1	1

2) Знайдемо ДДНФ двома способами.

а) за допомогою таблиці істинності:

1. З таблиці видно, що наборів, на яких функція набуває значення 1, п’ять:

, , , , .

2. Для кожного набору утворимо відповідну повну елементарну кон’юнкцію:

, , , , , або

, , , , .

3. З'єднаємо отримані повні елементарні кон’юнкції знаками :

– отримали ДДНФ.

б) за допомогою рівносильних перетворень:

– позбавимося у формулі від входження знаку :

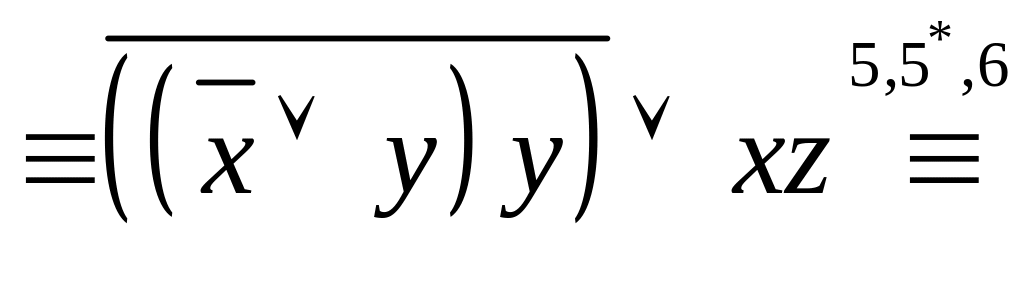– доб'ємося того, щоб знак стояв тільки перед змінними:

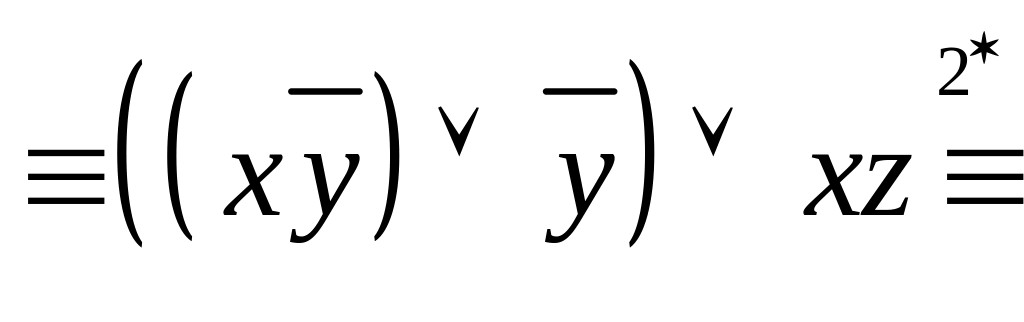
– отримали ДНФ, елементарні кон’юнкції якої поповнимо до повних:

– з однакових членів отриманої диз’юнкції залишаємо тільки один:

– отримали ДДНФ.

Знайдемо ДКНФ двома способами:

а) за допомогою таблиці істинності.

1. З таблиці видно, що наборів, на яких функція набуває значення 0, три:

, , .

2. Для кожного набору утворимо відповідну повну елементарну диз’юнкцію:

, , , або

, , .

3. З'єднаємо отримані повні елементарні диз’юнкції знаками :

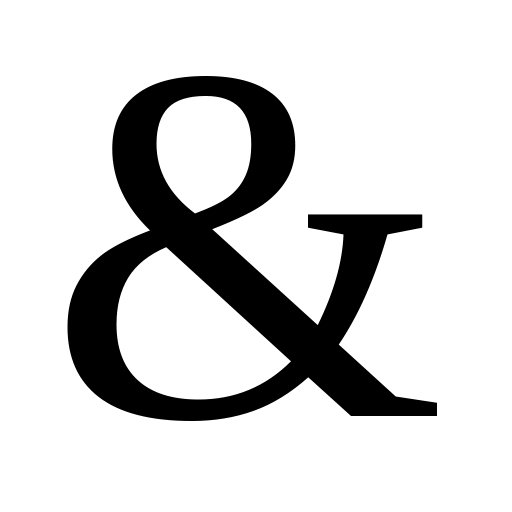– отримали ДКНФ.

б) за допомогою рівносильних перетворень:

– позбавимося у формулі від входження знаку :

– доб'ємося того, щоб знак стояв тільки перед змінними:

– отримали ДНФ, з якої за дистрибутивністю отримаємо КНФ:

– отримали КНФ, елементарні диз’юнкції якої поповнимо до повних:

– з однакових членів отриманої кон’юнкції залишаємо тільки один:

– отримали ДКНФ.

3) Знайдемо зображення даної функції у вигляді многочлена Жегалкіна.

Повна система булевих функцій – така система, що будь-яка булева функція може бути записана у вигляді формули через функції цієї системи. (Тобто будь-яка булева функція є складеною функцією функції цієї системи).

Приклади повних систем: , , , , , .

Многочлен Жегалкіна – це вираз вигляду , , де – стала 1 або 0 (звичайно 0 не пишуть) і при – попарно різні елементарні кон’юнкції, які не містять заперечень.

Загальний вигляд многочлена Жегалкіна від двох змінних:

.

Загальний вигляд многочлена Жегалкіна від трьох змінних:

.

Методи зображення булевої функції многочленом Жегалкіна:

1. Метод заміни зручний, коли функція задана формулою. Булеву функцію зображаємо формулою у ДДНФ над системою і робимо заміну , .

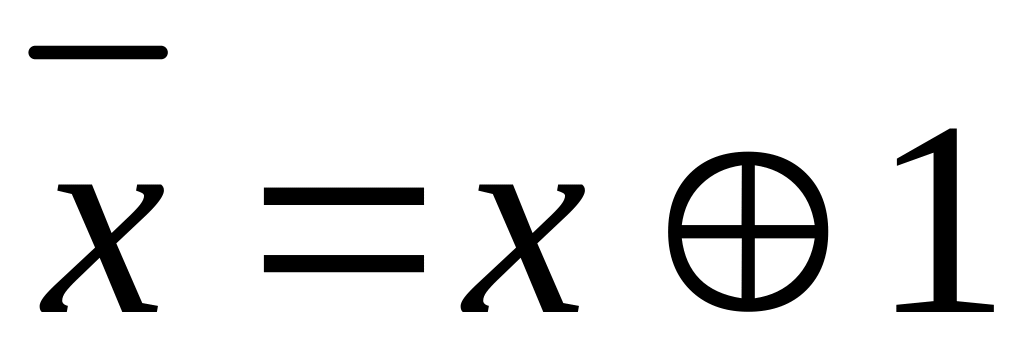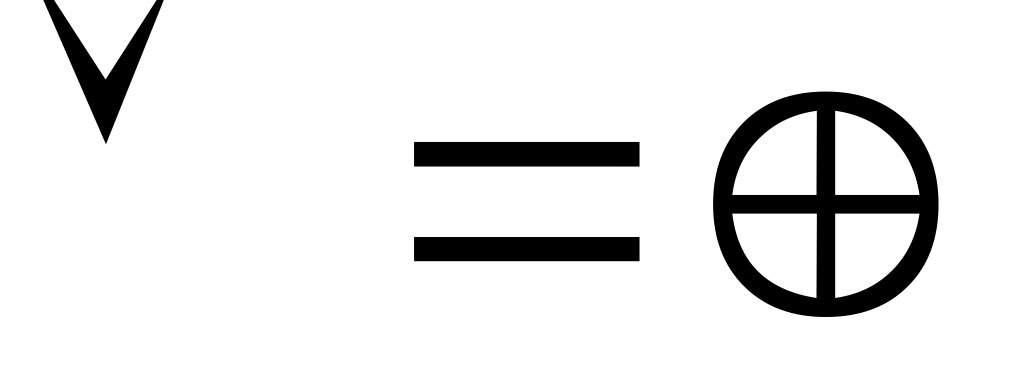2. Метод невизначених коефіцієнтів зручний, коли функція задана таблицею. Визначаємо коефіцієнти у загальному вигляді многочлену Жегалкіна, використовуючи значення функції на всіх наборах. Підставляємо в обидві частини різні значення змінних, отримаємо систему лінійних рівнянь (одне рівняння для кожного рядка таблиці). Розв’язавши систему, підставляємо знайдені коефіцієнти в многочлен.

3. Метод трикутника Паскаля зручний, коли функція задана вектором своїх значень. Коефіцієнти многочлена Жегалкіна можна отримати за допомогою трикутника Паскаля, побудованого за вектором значень функції, по одиницях його лівої сторони.

І спосіб. Застосуємо метод заміни, за яким в формулі у ДДНФ робимо заміну , .

– замінимо на , на :

– розкриємо дужки:

– приведемо подібні, пам’ятаючи, що парне число однакових доданків в сумі за модулем 2 дає 0:

– многочлен Жегалкіна.

ІІ спосіб. Застосуємо метод невизначених коефіцієнтів. Запишемо функцію у вигляді многочлена Жегалкіна від трьох змінних у загальному вигляді:

.

Визначимо коефіцієнти, використовуючи значення функції на всіх наборах. Підставимо в обидві частини різні значення змінних , отримаємо систему рівнянь (одне рівняння для кожного рядка таблиці).

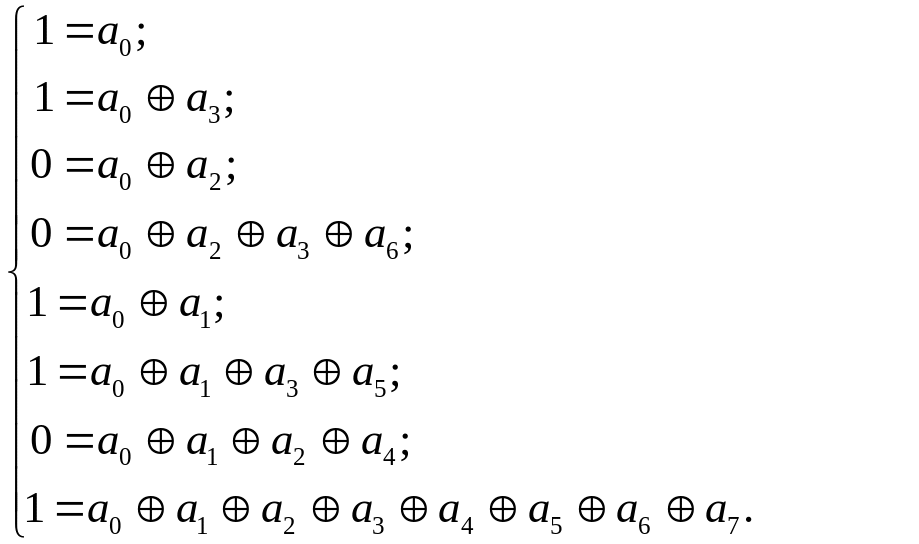
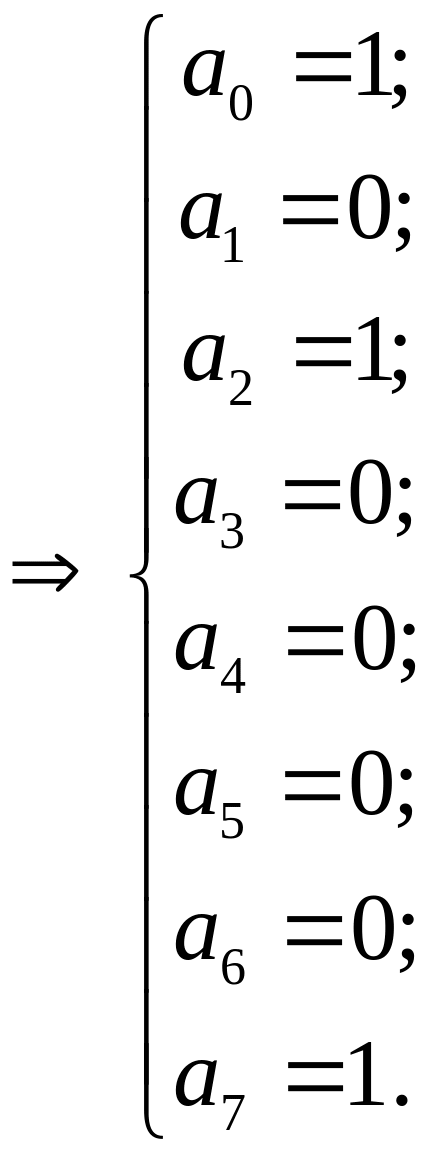
Розв’язавши систему, підставимо знайдені коефіцієнти в многочлен. Отже, – многочлен Жегалкіна.

ІІІ спосіб. Застосуємо метод трикутника Паскаля по одиницях його лівої сторони за таблицею істинності функції.

			трикутник Паскаля
0	0	0	1 1 0 0 1 1 0 1
0	0	1	0 1 0 1 0 1 1
0	1	0	1 1 1 1 1 0
0	1	1	0 0 0 0 1
1	0	0	0 0 0 1
1	0	1	0 0 1
1	1	0	0 1
1	1	1	1

Верхня сторона трикутника є вектор значень функції. Будь-який інший елемент трикутника є сума за модулем 2 двох сусідніх елементів попереднього рядка. Ліва сторона трикутника містить три одиниці. Отже, многочлен Жегалкіна буде містити три доданки. Перша одиниця трикутника відповідає набору (0 0 0). Отже, перший доданок многочлена Жегалкіна є 1. Друга одиниця трикутника відповідає набору (0 1 0). Отже, другий доданок многочлена Жегалкіна є . Третя одиниця трикутника відповідає набору (1 1 1). Отже, третій доданок многочлена Жегалкіна є .

Остаточно маємо:

– многочлен Жегалкіна.

Завдання № 4. Орграф заданий матрицею суміжності

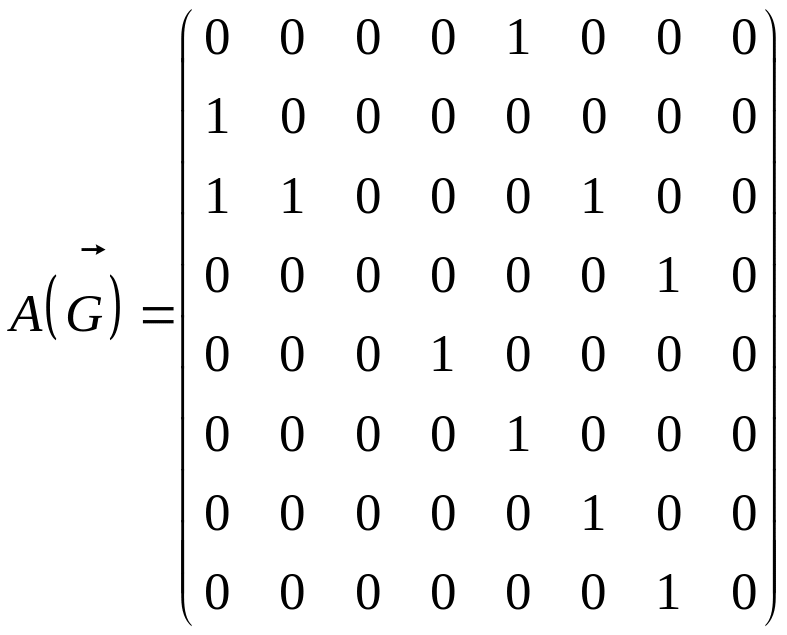
Треба:

1. намалювати орграф;

2. знайти всі шляхи довжини 2 і 3;

3. знайти матрицю досяжності ;

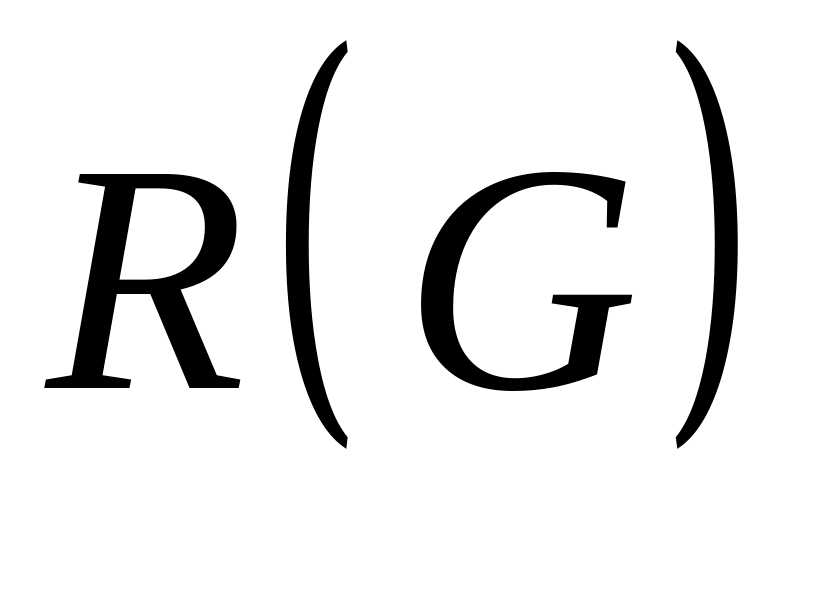4. знайти компоненти зв’язності та сильної зв’язності;

5. побудувати граф конденсації 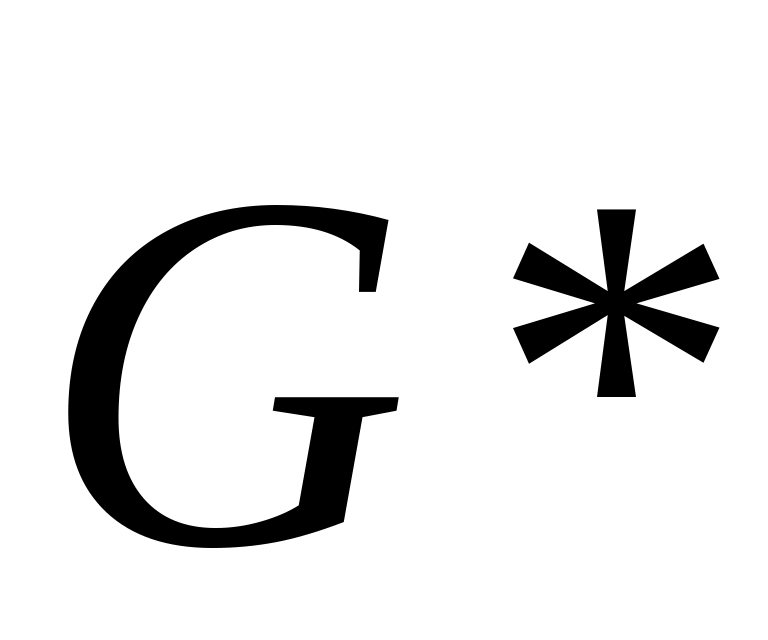графа ;

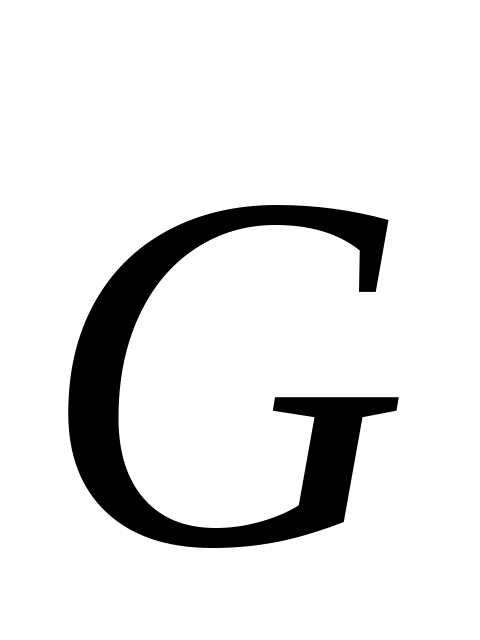6. визначити тип зв’язності графа ;

7. знайти матрицю інцидентності ;

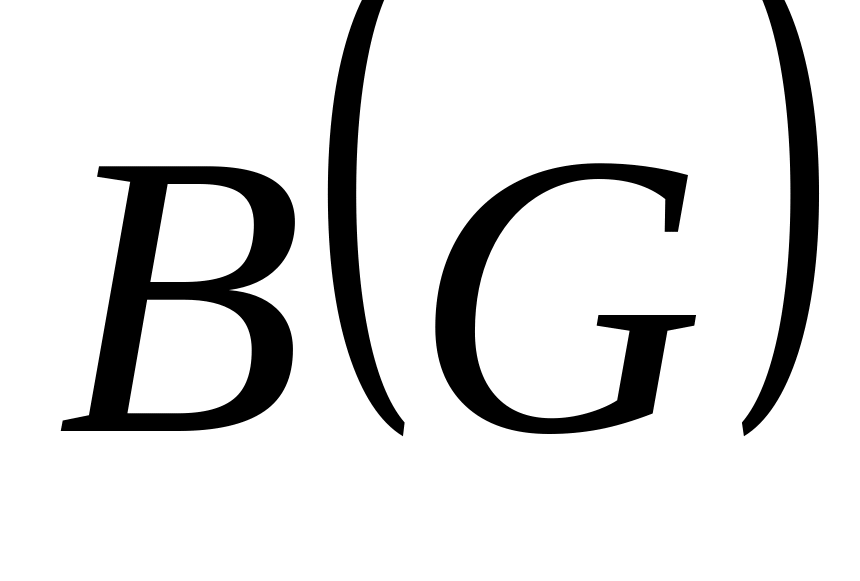8. знайти степені вершин , , , ;

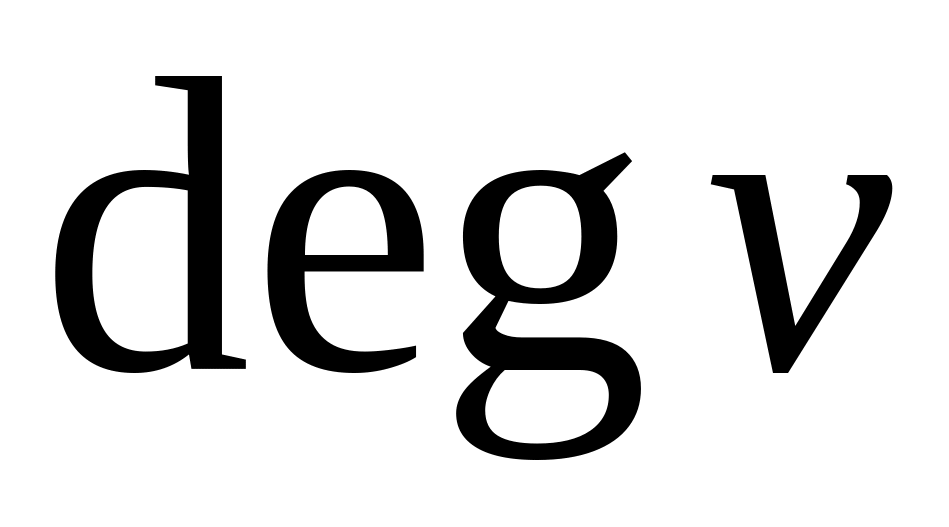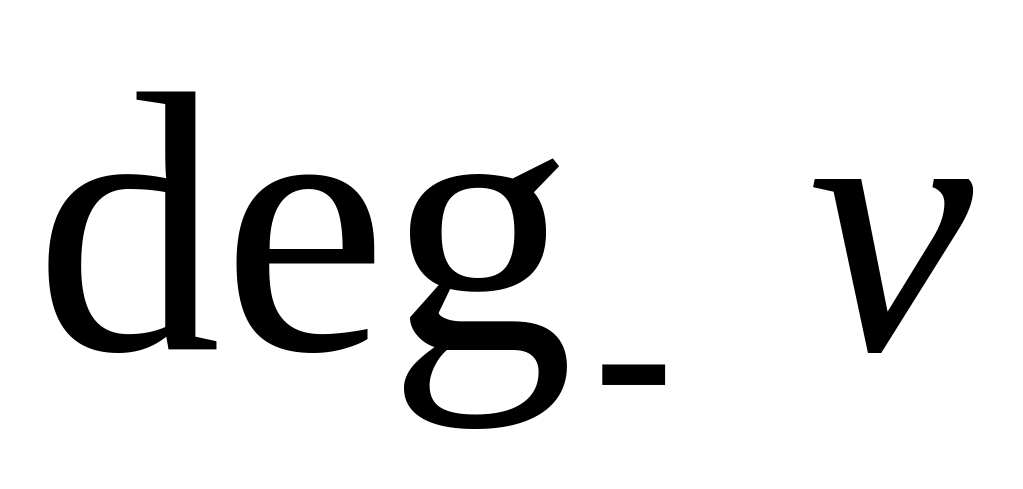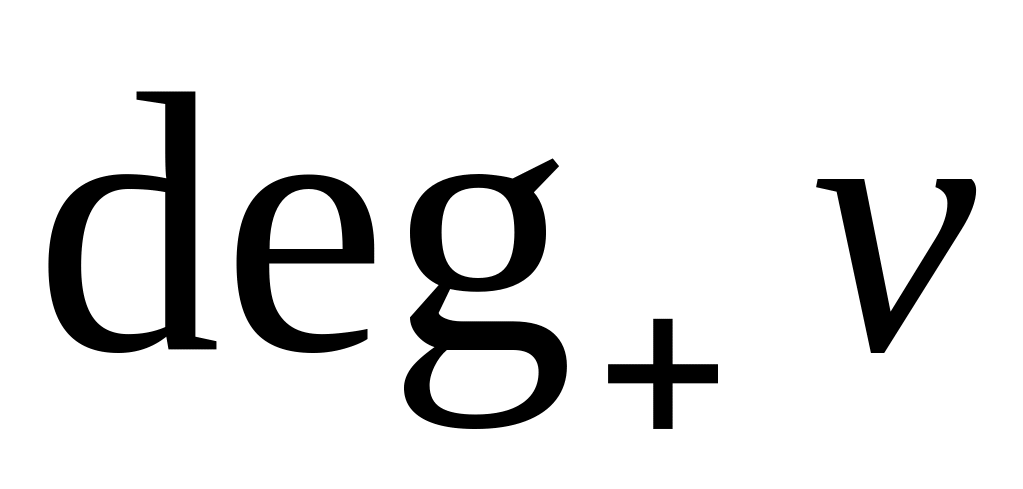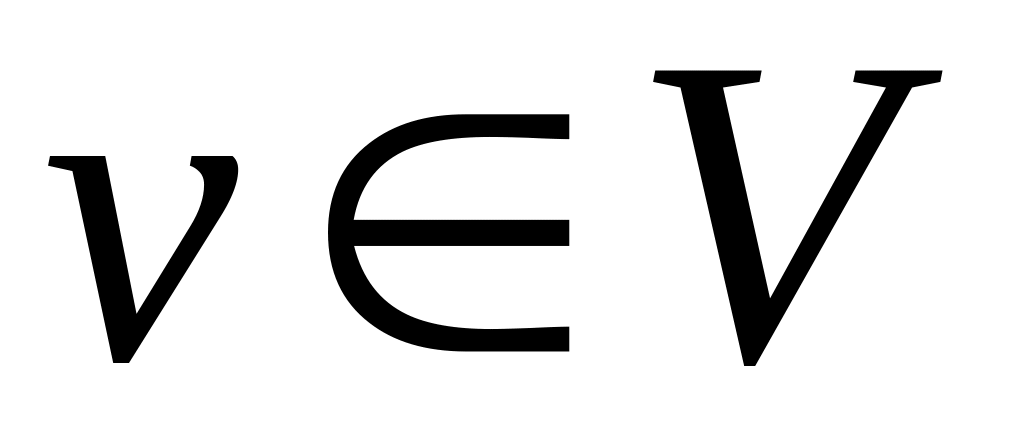9. знайти ейлерів цикл в асоційованому графі 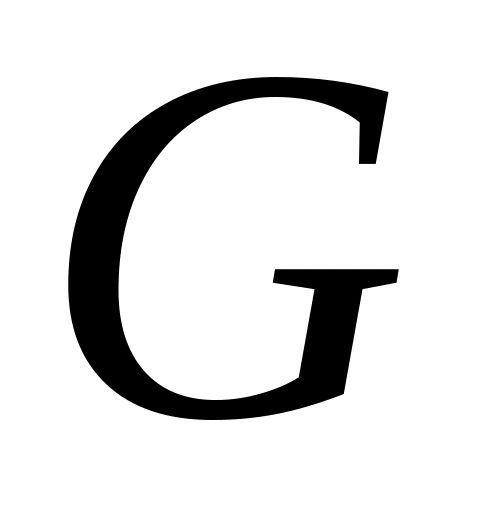(графі, отриманому з скасуванням орієнтації). Якщо такого циклу в графі нема, то вилучити мінімально можливе число дуг, і в новому орграфі знайти такий цикл.

Розв’язання.

1. Намалюємо орграф:

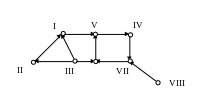
2. Знайдемо в графі всі шляхи довжини 2. Для цього матрицю суміжності 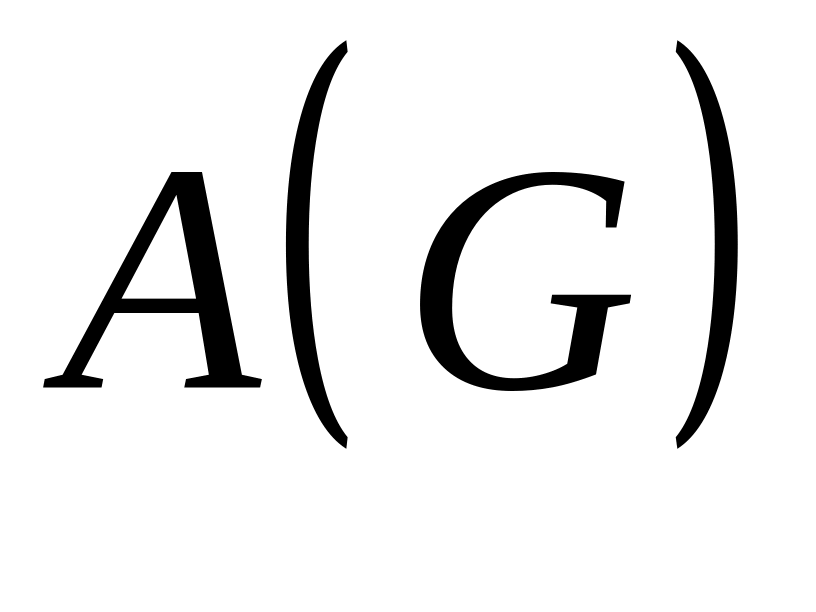піднесемо до другого степеня:

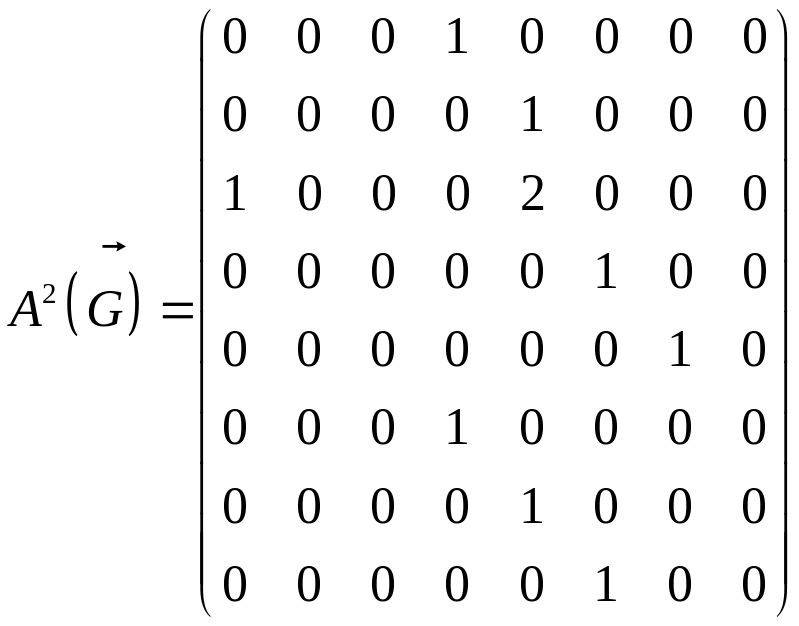
Оскільки елемент в матриці дорівнює 1, в існує один шлях довжини 2 з вершини І у вершину ІV. Це шлях І,V, ІV.

Оскільки елемент в матриці дорівнює 1, в існує один шлях довжини 2 з вершини ІІ у вершину V. Це шлях ІІ, І, V.

Оскільки елемент в матриці дорівнює 2, в існує два шляхи довжини 2 з вершини ІІІ у вершину V. Це шляхи ІІІ, І, V і ІІІ, VІ, V.

Аналогічно знаходяться інші шляхи довжини 2:

з вершини ІІІ у вершину І: ІІІ, ІІ, І;

з вершини ІV у вершину VІ: ІV, VІІ, VІ;

з вершини V у вершину VІІ: V, ІV, VІІ;

з вершини VІ у вершину ІV: VІ, V, ІV;

з вершини VІІ у вершину V: VІІ, VІ, V;

з вершини VІІІ у вершину VІ: VІІІ, VІІ, VІ.

Знайдемо в графі всі шляхи довжини 3. Для цього матрицю суміжності піднесемо до третього степеня:

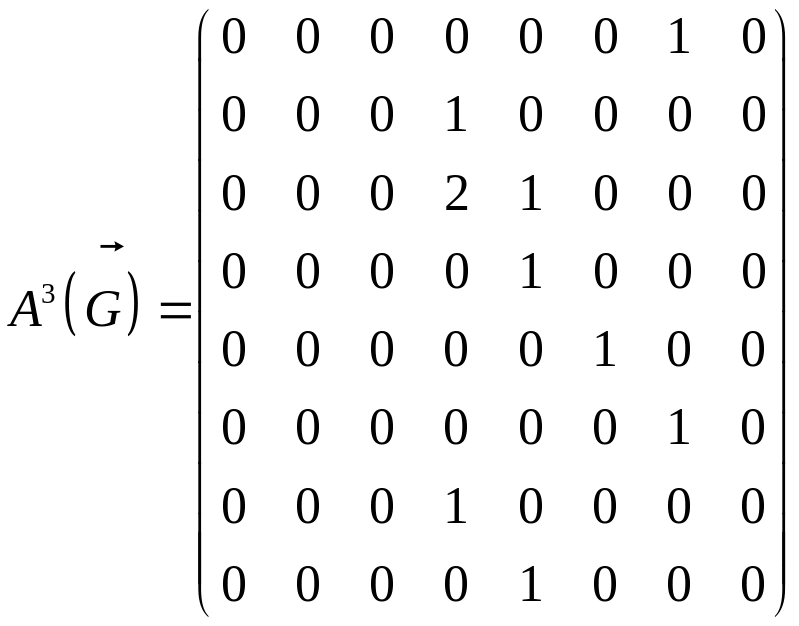
Оскільки елемент в матриці дорівнює 1, в існує один шлях довжини 3 з вершини І у вершину VІІ. Це шлях І, V, ІV, VІІ.

Оскільки елемент в матриці дорівнює 1, в існує один шлях довжини 3 з вершини ІІ у вершину ІV. Це шлях ІІ, І, V, ІV.

Оскільки елемент в матриці дорівнює 2, в існує два шляхи довжини 3 з вершини ІІІ у вершину ІV. Це шляхи ІІІ, І, V, ІV і ІІІ, VІ, V, ІV.

Аналогічно знаходяться інші шляхи довжини 3:

з вершини ІІІ у вершину V: ІІІ, ІІ, І, V;

з вершини ІV у вершину V: ІV, VІІ, VІ, V;

з вершини V у вершину VІ: V, ІV, VІІ, VІ;

з вершини VІ у вершину VІІ: VІ, V, ІV, VІІ;

з вершини VІІ у вершину ІV: VІІ, VІ, V, ІV;

з вершини VІІІ у вершину V: VІІІ, VІІ, VІ, V.

3. Побудуємо матрицю досяжності . Для цього обчислимо вираз

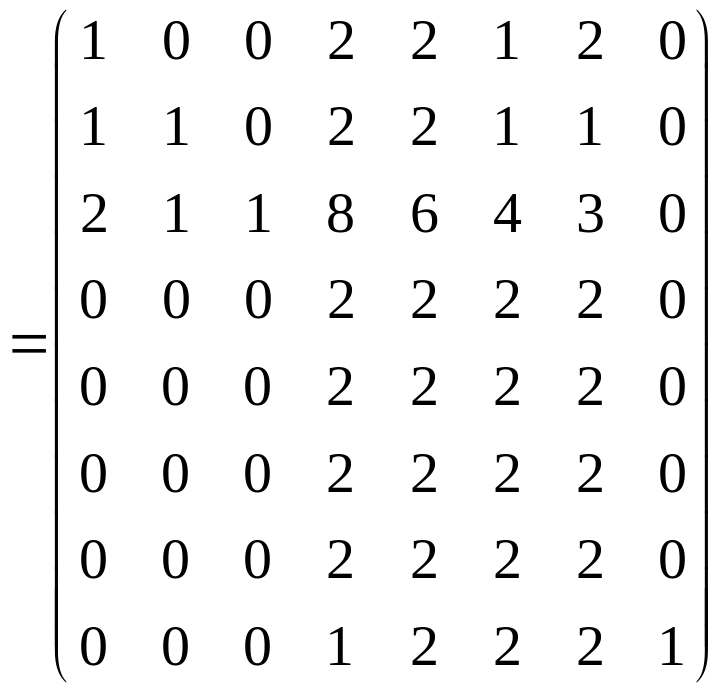
і застосуємо до нього булеве відображення:

4. Використаємо матрицю досяжності для виявлення компонентів зв’язності графа . Обчислимо матрицю 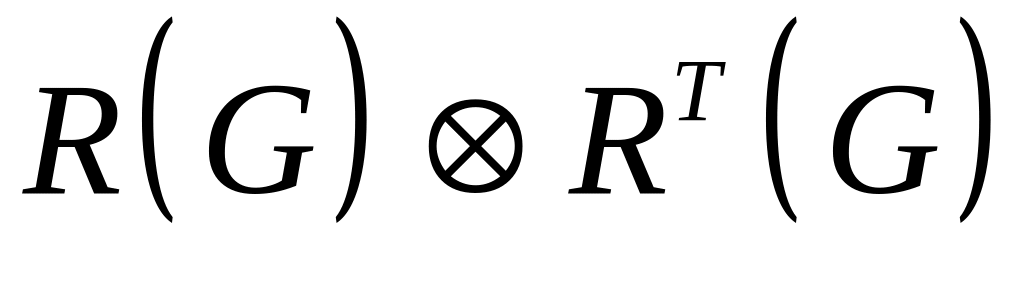, де – поелементне множення матриць:

.

Ця матриця має блоково-діагональий вигляд, де кожний блок визначає сильну компоненту зв’язності. Так, вершина І складає одну сильну компоненту зв’язності. Вершини ІІ і ІІІ, яким відповідають одиниці на головній діагоналі матриці , також складають сильні компоненти зв’язності. Вершини ІV, V, VІ, VІІ складають одну сильну компоненту зв’язності, оскільки їм відповідає один блок в матриці . Вершина І складає ще одну сильну компоненту зв’язності.

Піднесемо матрицю досяжності до другого степеня:

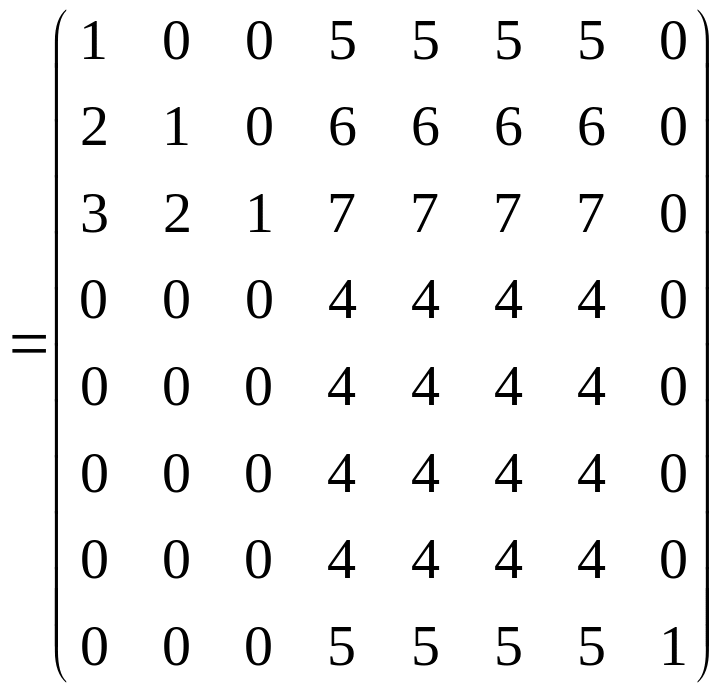
Діагональні елементи матриці показують число елементів в тій сильній компоненті зв’язності, в яку входить вершина і.

5. Побудуємо граф конденсації графа . Для цього позначимо сильні компоненти графа наступним чином:

,

,

,

,

.

Граф конденсації графа має вигляд:

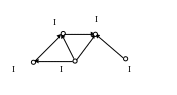
6. Визначимо тип зв’язності графа . Це легко зробити за графом конденсації . Оскільки в графі є вершини, жодна з яких не досяжна з іншої, наприклад, і , то граф є слабко зв’язаним.

7. Знайдемо матрицю інцидентності графа . Для цього позначимо дуги графа наступним чином:

Елемент матриці інцидентності дорівнює -1, якщо дуга виходить з вершини , дорівнює 1, якщо дуга входить у вершину , і дорівнює 0, якщо дуга не є інцидентною вершині .

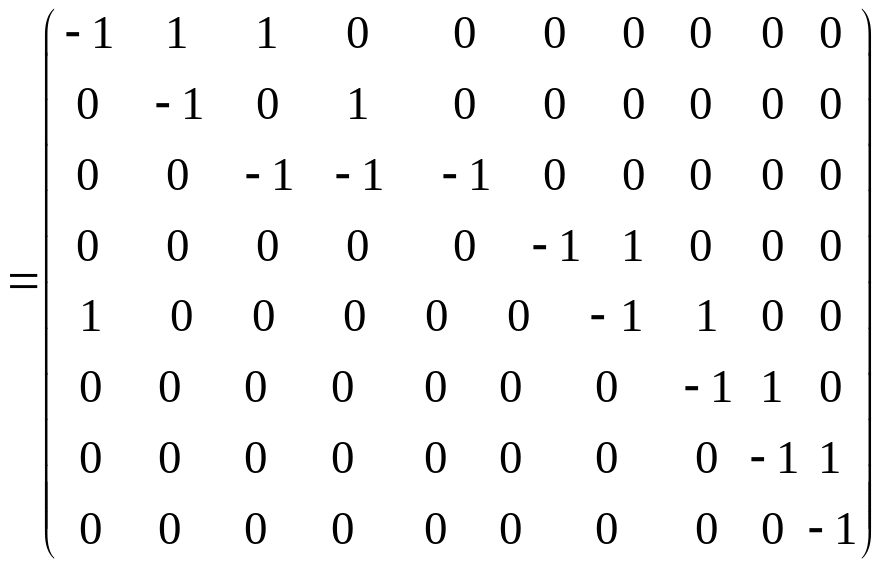
8. Знайдемо степені вершин , , , .

, , ,

, , ,

, , ,

, , ,

, , ,

, , ,

, , ,

, , .