1. Физическая химия — раздел химии, наука об общих законах строения, структуры и превращения химических веществ. Исследует химические явления с помощью теоретических и экспериментальных методов физики.

Физическая химия является основным теоретическим фундаментом современной химии, использующим теоретические методы таких важнейших разделов физики, как квантовая механика, статистическая физика и термодинамика, нелинейная динамика, теория поля и др. Она включает учение о строении вещества, в том числе: о строении молекул, химическую термодинамику, химическую кинетику и катализ. В качестве отдельных разделов в физической химии выделяют также электрохимию, фотохимию, физическую химию поверхностных явлений (в том числе адсорбцию), радиационную химию, учение о коррозии металлов, физико-химию высокомолекулярных соединений и др. Весьма близко примыкают к физической химии и подчас рассматриваются как её самостоятельные разделы коллоидная химия, физико-химический анализ и квантовая химия. Большинство разделов физической химии имеет достаточно чёткие границы по объектам и методам исследования, по методологическим особенностям и используемому аппарату.

Кристаллохимия — это наука о кристаллических структурах и их связи с природой вещества.

Радиохимия – ведёт работу со сверхмалыми количествами веществ и с очень сильно разбавленными растворами, а также с источниками ионизирующих излучений.

Термохимия — раздел физической химии, изучающий закономерности протекания химических реакций во времени, зависимости этих закономерностей от внешних условий, а также механизмы химических превращений.

Фотохимия — часть химии высоких энергий, раздел физической химии — изучает химические превращения (химия возбужденных состояний молекул, фотохимические реакции), протекающие под действием света в диапазоне от дальнего ультрафиолета до инфракрасного излучения.

Химическая термодинамика — раздел физической химии, изучающий процессы взаимодействия веществ методами термодинамики.

Радиационная химия — часть химии высоких энергий, раздел физической химии — изучает химические процессы, вызываемые воздействием ионизирующих излучений на вещество.

Электрохимия — раздел химической науки, в котором рассматриваются системы и межфазные границы при протекании через них электрического тока, исследуются процессы в проводниках, на электродах (из металлов или полупроводников, включая графит) и в ионных проводниках (электролитах).

2. Коллоидная химия — наука, являющаяся разделом химии, изучающая дисперсные системы, коллоиды и поверхностные явления, возникающие на границе раздела фаз. Физикохимия дисперсных систем и растворов высокомолекулярных соединений. Основоположником коллоидной химии принято считать Т. Грэма, который в 1861 году первые ввёл термин коллоидная химия и «коллоид». Основная задача данной науки — установление законов, управляющих явлениями, протекающими в коллоидных системах. Коллоидная химия неразрывно связана с физической химией (образуя физколлоидную химию), общей химией (органической и неорганической), физикой и биологией. Таким образом, коллоидная химия изучает коллоидные системы, содержащие относительно крупные частицы от 0,001 до 0,1 мкм.

Медико-биологический аспект. Научное значение коллоидной химии особенно велико для биологии и медицины в связи с изучением физико-химических свойств коллоидных растворов и студней, образуемых белками и другими биополимерами, играющими большую роль в свойственных живым организмам процессах обмена веществ. Нормальное или патологическое функционирование организма человека во многом определяется характером протекания коллоидных процессов. Учитывая, что организм человека, животных и растений содержит такие высокомолекулярные вещества как белки, нуклеиновые кислоты, крахмал, гликоген, пектины, целлюлозу и др., а их растворы являются коллоидными растворами, можно без преувеличения сказать, что коллоидная химия изучает материальную основу систем, без которых нельзя себе представить ни существование всех живых существ, ни основ всей современной промышленности и техники. В биологических и медицинских исследованиях широко используются методы коллоидной химии: диализ и особенно электродиализ, применяющийся для очистки и изучения ферментов, гормонов, вирусов, токсинов, антибиотиков, антител и пр.; ультрафильтрация, используемая для разделения и фракционирования сложных полидисперсных систем; коагуляция, с помощью которой определяют состояние полидисперсных систем крови и других биологических жидкостей: ультрацентрифугирование, широко используемое для получения физико-химических характеристик белков и других высокомолекулярных биологически активных соединений.

3. Эмпирическая температура – это температура, определение которой основано на зависимости от температуры некоторых физических свойств вещества, подлежащих непосредственному измерению. Закон Шарля или второй закон Гей-Люссака — один из основных газовых законов, описывающий соотношение давления и температуры для идеального газа. Экспериментальным путем зависимость давления газа от температуры при постоянном объёме установлена в 1787 году Шарлем и уточнена Гей-Люссаком в 1802 году. Если температура газа увеличивается, то и его давление тоже увеличивается, если при этом масса и объём газа остаются неизменными. Закон имеет особенно простой математический вид, если температура измеряется по абсолютной шкале, например, в градусах Кельвина. Математически закон записывают так: P~T или p/t=k где: P — давление газа, T — температура газа (в градусах Кельвина), k — константа. Этот закон справедлив, поскольку температура является мерой средней кинетической энергии вещества. Если кинетическая энергия газа увеличивается, его частицы сталкиваются со стенками сосуда быстрее, тем самым создавая более высокое давление.

4. Уравнение Гей-Люсака.

При постоянном давлении объем данного количества газа прямо пропорционален температуре: V~T, при Р = const. График этой зависимости проходит через начало координат и, соответственно, при 0К его объём станет равным нулю, что очевидно не имеет физического смысла. Это привело к предположению, что -273⁰С – минимальная температура, которую можно достичь. Абс. 0 служит началом отсчета температурной шкалы. В рамках термодинамики абс. 0 на практике недостижим.

Абсолютный нуль температуры (реже — абсолютный ноль температуры) — минимальный предел температуры, которую может иметь физическое тело во Вселенной. Абсолютный нуль служит началом отсчёта абсолютной температурной шкалы, например, шкалы Кельвина. 

В рамках применимости термодинамики абсолютный нуль на практике недостижим. Его существование и положение на температурной шкале следует изэкстраполяции наблюдаемых физических явлений, при этом такая экстраполяция показывает, что при абсолютном нуле энергия теплового движения молекул и атомов вещества должна быть равна нулю, то есть хаотическое движение частиц прекращается, и они образуют упорядоченную структуру, занимая чёткое положение в узлахкристаллической решётки (жидкий гелий составляет исключение). Однако, с точки зрения квантовой физики и при абсолютном нуле температуры существуют нулевые колебания, которые обусловлены квантовыми свойствами частиц и физического вакуума, их окружающего.

5. Уравнение Менделеева-Клапейрона – формула, устанавливающая зависимость между давлением, молярным объемом и абсолютной температурой идеального газа. Газы нередко бывают реагентами и продуктами в химических реакциях. Не всегда удается заставить их реагировать между собой при нормальных условиях. Поэтому нужно научиться определять число молей газов в условиях, отличных от нормальных. Для этого используют уравнение состояния идеального газа PV_M = nRT, где р – давление, V_M – молярный объем, R – универсальная газовая постоянная, T – абс. темп-ра, n – кол-во вещества.

6. Уравнение состояния газа Ван-дер-Ваальса.

Называется так, потому что мера основного состояния нижнего предела температуры — абсолютный ноль, то есть наиболее низкая возможная температура, при которой в принципе невозможно извлечь из вещества тепловую энергию. Абсолютный ноль определён как 0 K, что равно −273.15 °C. Шкала энергии выбирается так, что за начало отсчета берется E (d) – положение центра тяжести всех пяти d - орбиталей, которое остается неизменным под действием поля лигандов. Поэтому, если d - электрон попадает на орбиталь t2g, то комплекс становится на 0 4Д более стабильным, чем следует из простой электростатической модели — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса. Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах, в других условиях её соответствие с опытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные — не могут. Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия становится функцией не только температуры, но и объёма. Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой.(P+a*ню^2/V^2)(V-bню)=нюRT (для ню молей газа). Чтобы как-то устранить причины, из-за которых уравнение идеального газа практически неприменимо для описания поведения реальных газов, Ван-дер-Ваальс в 1879 году предложил включить в него два дополнительных члена – а и b: константу а добавляют к Р для того, чтобы учесть (скомпенсировать) уменьшение давления из-за межмолекулярного притяжения; константа b учитывает эффективный объем молекул газа, и она вычитается из _. Обе константы подбирались эмпирически. В результате для одного моля газа уравнение приобретает вид: . Однако в этом уравнении появились еще некоторые члены. Так, поправка к давлению принята равной по той причине, что молекулы на поверхности газа притягиваются не только друг к другу (к молекулам на поверхности), но и к молекулам, находящимся внутри. Сила притяжения зависит от плотности газа как на поверхности, так и внутри. Поскольку плотность – это масса/V, то ее влияние можно учесть умножением константы а на 1/V². Поправка b в реальном случае примерно в 4 раза превышает собственный объем молекул моля газа. Ее иногда называют исключенным объемом, так как она соответствует пространству, реально исключаемому одним молем плотно упакованных молекул. Поправки а и b для любого газа приводятся в расчете на 1 моль. Если количество газа больше или меньше одного моля, необходимо пользоваться следующим уравнением: .

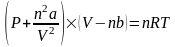7. Законы Дальтона. Он основан на том, что в смеси газов каждый газ оказывает такое же давление, какое он оказывал бы, если бы в сосуде присутствовал один. Давление компонентов газовой смеси зависит только от числа молей каждого из них, так как температура и объем для всех газов в смеси одинаков — два физических закона, определяющих суммарное давление и растворимость смеси газов. Закон о суммарном давлении смеси газов: давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений: P= =p1+p2+…+p_n Закон о растворимости компонентов газовой смеси: при постоянной температуре растворимость в данной жидкости каждого из компонентов газовой смеси, находящейся над жидкостью, пропорциональна их парциальному давлению: m_i = . Оба закона Дальтона строго выполняются для идеальных газов. Для реальных газов эти законы применимы при условии, если их растворимость невелика, а поведение близко к поведению идеального газа. 8. Типы систем и процессов, функции состояния, работа, внутренняя энергия, теплота. Под понятием энергия обычно понимают способность производить работу. Решая какую-либо задачу методами термодинамики, необходимо прежде всего выделить из окружающего мира какую-то систему. Это может быть дождевая капля, двигатель, организм, планета и т.д. Если говорят, что выделенная система гомогенна, это означает, что свойства системы одинаковы во всех частях, и система непрерывна от точки к точке. Если говорят, что система гетерогенна, это означает, что в ней присутствует не менее двух областей, называемых фазами, которые отделены друг от друга поверхностями, называемыми границами раздела. Системы бывают трех типов: открытые, закрытые и изолированные. В закрытой системе во время процесса происходит изменение энергии, но масса остается постоянной. В открытой системе может изменяться как энергия, так и масса. В изолированной системе не происходит обмена с окружающей средой ни массой, ни энергией. Очень часто в термодинамике сталкиваются с понятием равновесие. Если состав и свойства системы достаточно долго не меняются, то говорят, что система находится в равновесии. Однако химическое равновесие не является состоянием покоя. Это состояние, в котором реакция протекает как в одну, так и в другую сторону, но с одинаковыми скоростями. Состояние системы определяется ее свойствами. Если изменяется одно из свойств, состояние системы меняется. При изучении системы обычно рассматриваются такие свойства, которые легко измерить. Это, в частности, температура, давление, объем, состав. Некоторые свойства взаимосвязаны, поэтому нет необходимости измерять их все одновременно. Химические процессы обычно сопровождаются поглощением или выделением тепла. Реакции с выделением тепла называются экзотермическими, реакции с поглощением тепла – эндотермическими. Количество тепла пропорционально массе прореагировавших веществ, поэтому сравнение количества тепла, выделяющегося в реакции, относят к единице количества вещества. Обычно это 1 моль. Экспериментально теплоты химических реакций определяют при постоянном объеме Q_v или постоянном давлении Q_p.

9. Первый закон термодинамики. Формулировки, способы выражения. Первое начало термодинамики – это закон сохранения энергии. Он впервые четко сформулирован Г. Гельмгольцем в 1847 году. Есть несколько формулировок первого закона термодинамики. Если одна из них принимается в качестве основной, то все другие являются следствиями, вытекающими из нее. Одна из формулировок звучит следующим образом: энергия не создается и не уничтожается. Возможны лишь превращения энергии из одного вида в другой в строго эквивалентных количествах. Следствием из этого закона является вывод, что невозможен вечный двигатель первого рода, т.е. нельзя создать такой двигатель, который совершил бы работу без затраты энергии. Создание такого двигателя возможно только в том случае, если неверен первый закон. Часто используется еще одна формулировка первого начала термодинамики: внутренняя энергии изолированной системы есть величина постоянная. Если данной системе передается некоторое количество энергии в форме тепла Q, которое идет только на приращение внутренней энергии системы U и на совершение системой работы W, то, согласно первому началу, Q = U + W, (2.1) для бесконечно малых изменений Q = dU + W, (2.2). Уравнения (2.1) и (2.2) являются математическим выражением первого начала термодинамики. ΔU и dU не зависят от пути перехода системы из начального состояния в конечное, т.е. внутренняя энергия является функцией состояния системы. Если система совершает работу W только против внешнего давления, то W = PΔV или для элементарного процесса δW = PdV. Математическое выражение первого закона термодинамики в этом случае имеет вид: Q = ΔU + PdV.