Предмет начертательной геометрии. Методы проецирования.

Комплексный чертеж точки

• Предмет начертательной геометрии.

• Методы проецирования. Прямая и обратная задачи начертательной геометрии.

• Комплексный чертеж точки.

Литература

Бубенников А.В. Начертательная геометрия. – М.: Высшая школа, 1985 – 288 с.

(с.3-40)

Фролов С.А. Начертательная геометрия. – М.: Высшая школа, 1983 – 215 с.

Чекмарев А.А. Инженерная графика. – М.: Высшая школа, 1988 – 335 с. (с. 21-28)

Лагерь А.И., Колесникова Э.А. Инженерная графика. – М.: Высшая школа, 1985 с.- 176 с. (с. 6-27)

Крылов И.И. Начертательная геометрия. – М.: Высшая школа, 2001 – 224 с (с. 5-20)

1. 1 Предмет начертательной геометрии

Начертательная геометрия со времен ее основоположника Гаспара Монжа (1746-1818) завоевала себе достойное место в высшей школе как наука, без которой немыслимо формирование инженера.

Проявление инженерной деятельности в современной жизни многообразны. На производстве и в быту нас окружают объекты, созданные трудом инженера: станки и автомобили, суда и самолеты, жилые дома, бытовые приборы и т.д.

Имеется много точек зрения на то, что считать полем деятельности инженера, среди которых все же превалирует та, что инженер – прежде всего конструктор. Именно этот вид деятельности сильнее всего выделяет инженера из числа других членов творческого коллектива.

Творческая фантазия – вот, пожалуй, основное качество, характеризующее профессиональную деятельность инженера.

Великий Альберт Эйнштейн говорил, что творческая фантазия (и воображение) важнее знания, ибо последнее ограничено, тогда как воображение исследователя, по существу, безгранично и в высшей степени стимулирует технический прогресс.

Плодотворное творчество инженера, в какой бы области техники он не работал, невозможно без четкого представления в его сознании пространственных и плоских конфигураций, являющихся геометрическими моделями проектируемых объектов. Алгоритмы создания таких моделей определяются положениями «Начертательной геометрии», науки, являющейся одним из разделов геометрии.

Таким образом, начертательная геометрия – дисциплина, составляющая основу инженерного образования.

Предметом начертательной геометрии является наложение и обоснование способов построения пространственных фигур на плоскости. Начертательная геометрия является тем разделом геометрии, в котором изучаются методы изображения пространственных фигур на чертеже и алгоритмы решения позиционных, метрических и конструкторских задач.

1.2 Методы проецирования. Прямая и обратная задача начертательной геометрии

Основные элементы пространства и отношения между ними

К основным элементам пространства относятся: точка, прямая и плоскость. Ими определяются простые фигуры, из которых создаются более сложные объекты пространства.

Обозначение элементов пространства:

точки – А, В, С и т.д.;

прямые – а, b, с и т.д.;

плоскости - и т.д.

Между элементами пространства существуют следующие отношения:

тождественность (совпадение) -

инцидентность (принадлежность) -

параллельность -

перпендикулярность - .

Над элементами пространства можно выполнять следующие операции:

соединение -

пересечение - .

Существует несколько способов получения графических изображений. Среди них различают способы центрального и параллельного проецирования.

Аппарат проецирования:

• проецируемый объект (например, [AB])

• плоскость, на которой получается изображение объекта (плоскость проекций )

• проецирующие лучи (i)

Центральное проецирование – получение проекций с помощью проецирующих лучей, проходящих через центр проецирования S (Рисунок 1.1).

S – центр проекций; S

- проецирующие лучи;

- проекции точек А и В на плоскости

В₁

Рисунок 1.1

Параллельное проецирование (частный случай центрального проецирования).

Если центр проецирования S удален в бесконечность, то все проецирующие лучи становятся параллельными друг другу, а проецирование называется параллельным (Рисунок 1.2).

В случае параллельного проецирования задается направление проецирования S.

S

m

Рисунок 1.2

Параллельное проецирование делится на прямоугольное и косоугольное проецирования.

а) б) А S

А В

S

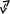
Рисунок 1.3

Ортогональное косоугольное проецирование – проецирование, при котором проецирующие лучи располагаются к плоскости проекций под углом отличным от прямого угла, рисунок 1.3 (а).

Ортогональное прямоугольное проецирование – частный случай параллельного проецирования. Проецирующие лучи перпендикулярны плоскости проекций, рисунок

1.3 (б).

Прямая задача начертательной геометрии заключается в получении проекций (изображений) геометрического образа и неразрывно связана с операцией проецирования.

Обратная задача заключается в восстановлении геометрического образа (его формы, положения и т.д.) по изображению.

Чертеж, позволяющий решать обратную задачу начертательной геометрии, называют обратимым. Обратимость – необходимое требование, предъявляемое к чертежу.

Однокартинный чертеж необратим: одна проекция не определяет положение точки в пространстве, т.к. отсутствует информация об удалении ее от плоскости проекций.