3.3.Гармонический анализ периодических сигналов

При разложении периодического сигнала s(t) в ряд Фурье в качестве ортогональной системы берут гармонические функции вида :

1, cos ₁t, sin ₁t, cos 2₁t, sin 2₁t,...

..., cos n₁t, sin n₁t,... (3.22)

или: ... , , 1 , , ... (3.23)

Интервал ортогональности в обоих случаях совпадает с периодом T = 2/₁ функции s(t).

Система функций Error: Reference source not found приводит к тригонометрической форме ряда Фурье, а система Error: Reference source not found - к комплексной форме. Между этими формами существует простая связь.

Воспользуемся системой комплексных гармоник Error: Reference source not found, тогда ряд Фурье будет иметь вид:

(3.24)

Совокупность коэффициентов C_n ряда Фурье в базисе тригонометрических функций называется частотным спектром периодического сигнала, а целью гармонического анализа как раз является нахождение коэффициентов ряда Фурье.

Коэффициенты ряда Error: Reference source not found легко определяются с помощью ранее встречавшихся формул - из формулы Error: Reference source not found следует, что квадрат нормы равен:

(3.25)

Таким образом, независимо от n, норма базисной функции .

Используя формулу для коэффициентов ряда Фурье Error: Reference source not found получим:

(3.26)

В Error: Reference source not found и Error: Reference source not found учтено, что для e^jn1t комплексно-сопряженной является функция e^-jn1t.

Коэффициенты C_n в общем случае являются комплексными величинами. Воспользуемся формулой Эйлера e^jx = cos x  j sin x,

, получим:

(3.27)

Отсюда косинусная - действительная часть коэффициента C_n:

(3.28)

а мнимая - синусная часть:

(3.29)

Коэффициенты С_n часто бывает удобно записывать в форме:

,

где (3.30)

(3.31)

Модуль C_n является четной функцией относительно n, а аргумент _n - нечетной (это следует из Error: Reference source not found и Error: Reference source not found). Используя модуль и аргумент, ряд Error: Reference source not found может быть записан:

(3.32)

Отсюда нетрудно перейти к тригонометрической форме ряда Фурье. Выделив из ряда Error: Reference source not found пару слагаемых, соответствующих n (например, n=2) и учитывая что _-2=-₂, а C_-2=C₂, получим для суммы:

(3.33)

Окончательно ряд Error: Reference source not found в тригонометрической форме записывается:

(3.34)

Смысл удвоения коэффициентов Фурье C_n в тригонометрическом ряде при n1 становится ясным, если представить себе сумму двух векторов равной длины и с противоположными аргументами (векто­ры вращаются с одинаковой скоростью n₁, но в разные стороны для положительных и отрицательных частот), и вычислить проекцию этой суммы на ось абсцисс.

После перехода к тригонометрической форме понятие "отрицательных частот" теряет смысл.

Нередко встречается другая форма записи:

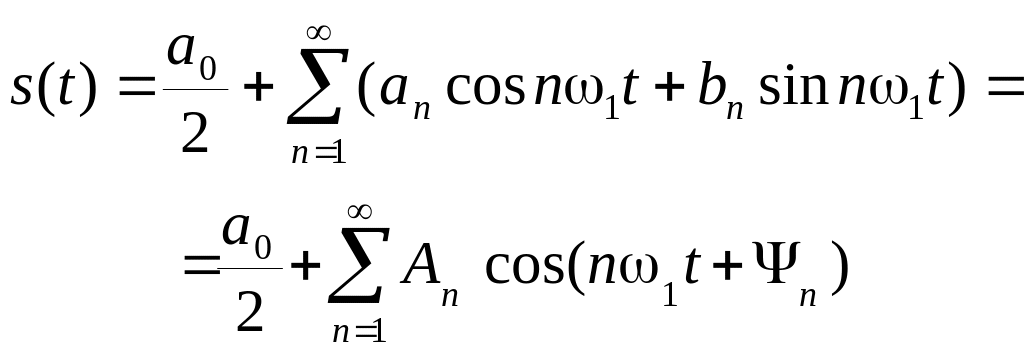(3.35)

где

Сравнивая Error: Reference source not found и Error: Reference source not found между собой, можно увидеть, что амплитуда n-й гармони­ки A_n связана с коэффициентом C_n  ряда (3.32):

A_n = 2C_n ; a_n= 2C_{n cos} ; b_n = 2C_{n sin}

Таким образом, для всех положительных n, включая и n=0:

(3.36)

Если сигнал представляет собой четную относительно t функцию, т.е. s(t)= s(-t), то в тригонометрической записи ряда остаются только косинусоидальные члены, так как коэффициенты b_n в соответствии с Error: Reference source not found обращаются в нуль.

Для нечетной относительно t функции s(t), наоборот, в нуль обращаются коэффициенты a_n и ряд состоит только из синусоидальных членов. Другими словами, четные функции имеют вещественный спектр, а нечетные - чисто мнимый.

Две характеристики - амплитудная и фазовая, то есть модули и аргументы комплексных коэффициентов ряда Фурье, полностью определяют структуру частот­ного спектра периодического колебания.

Спектр периодической функции называют линейчатым или дискретным, так как состоит из отдельных линий, соответствующих дискретным частотам 0, ₁, 2₁, 3₁ ... и так далее.