23. Условия наблюдения одноэлектронного туннелирования.

Доступное объяснение

Для наблюдения дискретной при­роды одноэлектронного переноса за­ряда на квантовую точку должны быть выполнены два условия. В соответст­вии с первым, электростатическая энергия квантовой точки в присутст­вии одного электрона e²/2C должна превосходить тепловую энергию k_BT случайных колебаний атомов. Второе состоит в удовлетворении принципа неопределенности Гейзенберга, который в рассматриваемом случае можно сформулировать следующим образом: произведение энергии конденсатора е²/2С и характерного времени его зарядки τ = R_TC должно превосходить посто­янную Планка

                        ΔEΔt= [e²/(2C)] R_TC

где R_T — туннельное сопротивление потенциального барьера. Эти два условия можно переписать в виде:

e²/(2C) >>k_BT                                                                              

R_T>> h/t²                                                                          

От декана

1. минимальное изменение энергии было больше температурных флуктуаций

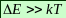отсюда следует

отсюда следует

2) Туннельное сопротивление должно быть больше квантовой единицы сопротивления

То есть не должно быть паразитного туннелирования

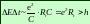
Для прочтения

Известно, что электрический ток в проводнике обуслов. движением электронов относительно неподвижных ионов решетки. В структуре, состоящей из двух обл. проводника, разделенных тон­ким д/э, электр. заряд переносится комбинированно - непре­рывно в проводнике и дискретно через д/э.

Первоначально граница раздела между проводником и диэлектриком электрически нейтральна. При приложении к внешним контактам структуры электрического потенциала начинается непрерывное изменение заряда в про­воднике. Оно сопровождается накоплением заряда на границе с д/э. Этот заряд возникает вследствие небольших непрерывных смещений электро­нов в приграничной области проводника относительно своих равновесных по­ложений. Накопление заряда продолжается до тех пор, пока его величина не окажется достаточной для отрыва и туннелирования через диэлектрик одного электрона. После акта туннелирования система возвращается в первоначальное состояние. При сохранении внешнего приложенного напряжения все повторя­ется вновь.

Электрон приобретает возможность туннелировать через д/э, ко­гда накопленный заряд становится больше +е/2 или меньше -е/2, поскольку только при этом уменьшается электростатическая энергия системы. Внутри этого интервала туннелирование невозможно из-за кулоновского взаи­модействия электрона с другими подвижными и неподвижными зарядами в проводнике. Данное явление называют кулоновской блокадой.

С труктура с одним туннельным барьером может быть представлена экви­в. схемой, показ. на рис. Ее основными элементами являют­ся емкость образованного диэлектриком конденсатора С_t, и туннельное сопротивление R_t, которое характеризует туннельный переход в отсутствие зарядо­вых эффектов. Емкость С_е является эквив. для подводящих электродов и источника U и учитывает изменение заряда в них при протекании I. Изменение электростатической энергии при туннелирова­нии одного электрона представляет собой разность между запасенной в конден­саторе энергией и работой, выполненной источником питания: ΔE=e²/2C-eV, где С = С_t + С_e. Тун-ие энергетически выгодно только тогда, когда ΔЕ < 0, что с учетом возможности тун-ия как при прямом, так и при обратном смещении приводит к выражению для порогового напряжения |Vt| = е/2С. Величину e²/2C называют кулоновским зазором.

ВАХ однобарьерной структуры показана на рис. Электр. ток в такой структуре появляется только при ее сме­щении напряжением больше порогового. На «открытом» участке ВАХ ток определяется величиной туннельного сопротив­ления Rt. Связанные с одноэлектронным туннелированием осцилляции напря­жения изменяют его величину на ± е/2С и происходят с частотой f = I/е, где I- протекающий электрический ток.

Экспериментальное наблюдение рассмотренных закономерностей воз­можно только при условии незначительности энергии тепловых флуктуаций в сравнении с энергией перезарядки конденсатора одним электроном. Это требу­ет выполнения условия к_вТ e₂/2С. Согласно ему при температуре 4 К вели­чина емкости туннельного барьера должна быть менее 10^-16 Ф, что реализуемо только в наноразмерных структурах. Второе, для проявления эффектов, связанных с одноэлектронным туннелированием в условиях кулоновской блокады, необходимо, чтобы туннельное сопротивление структуры Rt > h/e². Выполнение этого условия требуется для подавления квантовых флук­туаций количества электронов в квантовой точке, через которую происходит одноэлектронное туннелирование. То есть флуктуации должны быть достаточ­но малы для изменения заряда, чтобы он был устойчиво локализованным в кв. точке.