1. Предмет и задачи теории вероятностей.

Предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных явлений. Понятие «массовые» означает то, что закономерности случайных явлений проявляются, как правило, при их многократном воспроизведении. Свойство однородности указывает на то, что условия воспроизведения изучаемого явления должны быть фиксированы, иначе мы не обнаружим никаких устойчивых закономерностей исследуемого явления. Так при наблюдении чисел, выпадающих на игральном кубике, он должен быть недеформируемым. В противном случае закономерности выпадения того или иного числа на кубике (например, пластилиновом) будут меняться с каждым броском.

Основными задачами курса является изучение основных методов анализа закономерностей случайных явлений, формирование у будущих инженеров вероятностного мышления, умений и навыков решения производственных задач, принятия решений в условиях неопределённости.

2.Основные понятия теории вероятностей: массовые явления, стохастический эксперимент, случайное событие, элементарный исход; достоверное и невозможное события.

Все наблюдаемые нами события (явления) можно разделить на следующие три вида: достоверные, невозможные и случайные.

Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S.

Пример 1.1. Если в сосуде содержится вода при нормальном атмосферном давлении и температуре 20°, то событие {вода в сосуде находится в жидком состоянии} есть достоверное. В этом примере заданные атмосферное давление и температура воды составляют совокупность условий S.

Пример 1.2. Событие, состоящее в выпадении не более 6 очков при бросании одного игрального кубика, есть событие достоверное.Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена совокупность условий S.

Пример 1.3. Если будет осуществлена совокупность условий предыдущего примера, событие {вода в сосуде находится в твердом состоянии} заведомо не произойдет. Оно в данном случае событие невозможное.

Пример 1.4. Событие, состоящее в выпадении 10 очков при бросании одной игрального кубика, есть событие невозможное.

Невозможному событию соответствует пустое множество, поэтому его будем обозначать символом .

Случайным называют событие, которое при осуществлении совокупности условий S может произойти, либо не произойти. Пример 1.5. Если брошена монета, то она может упасть так, что сверху будет либо герб, либо надпись. Поэтому событие {при бросании монеты выпал герб}- случайное.Для обозначения случайных событий используются большие буквы начала латинского алфавита А, В, С, …, снабжая их при необходимости индексами.

Стохастическим называется эксперимент, результат которого заранее (до его проведения) предугадать нельзя. Часто вместо стохастического эксперимента говорят об испытании, опыте.

Пример 1.6. Рассмотрим опыт с бросанием игрального кубика с цифрами от 1 до 6 на гранях. Результатом этого стохастического эксперимента/опыта может быть появление одного из чисел 1, 2, 3, 4, 5, 6. Можно рассматривать и другие события, заключающиеся, например, в том, что выпадет четная/нечетная цифра, сумма выпавших чисел равна пяти, четная, делится на три и т.д.

Элементарным исходом называется элементарное, неразложимое событие. Любое событие может быть разложено на элементарные исходы; иначе говоря, событие есть совокупность элементарных исходов.

Пример 1.7. Событие, заключающееся в том, что сумма очков, выпавших при бросании двух игральных кубиков, равна шести, может состоять из элементарных событий, заключающихся в выпадении (1, 5), или (2, 4), или (3, 3), или 4, 2), или (5, 1). То есть, событие {сумма очков равна шести} разлагается на пять элементарных исходов.

Элементарные события обладают следующими свойствами:

• взаимно исключают друг друга, и в результате опыта обязательно происходит одно из этих элементарных событий;

• каково бы ни было случайное событие А, по наступившему элементарному событию можно сказать о том, произошло или не произошло событие А.

Элементарные события обозначают греческой буквой ω, снабжаемой при необходимости индексом, или строчными буквами конца латинского алфавита: x, y, z, …, снабжаемыми при необходимости индексами. Совокупность элементарных событий обозначают Ω и называют пространством элементарных событий.

Пример 1.8. В рассмотренном ранее примере 1.5 элементарными событиями ω_i можно считать появление любого числа от 1 до 6. Очевидно, что всего имеется 6 элементарных событий. Выбор элементарных событий определяется неоднозначно, чем можно пользоваться при решении задач.

В дальнейшем, вместо того чтобы говорить "совокупность условий S осуществлена", будем говорить кратко: "произведено "испытание". Таким образом, событие будет рассматриваться как результат испытания.

Пример 1.9. Стрелок стреляет по мишени, разделенной на четыре области. Выстрел – это испытание. Попадание в определенную область мишени - событие. В урне имеются цветные шары. Из урны наугад берут один шар. Извлечение шара из урны есть испытание. Появление шара определенного цвета - событие.

1.2. Виды случайных событий

События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

Пример 1.10. Из ящика с деталями наугад извлечена деталь. Появление стандартной детали исключает появление нестандартной детали. События {появилась стандартная деталь} и {появилась нестандартная деталь}-несовместные.

Пример 1.11. Брошена монета. Появление "герба" исключает появление цифры. События {появился герб} и {появилась цифра} - несовместные.

Несколько событий образуют полную группу, если в результате испытания появится, хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности, если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий. Этот частный случай представляет для нас наибольший интерес, поскольку используется далее.

Пример 1.12. Приобретены два билета денежно-вещевой лотереи. Обязательно произойдет одно и только одно из следующих событий: {выигрыш выпал на первый билет и не выпал на второй}, {выигрыш не выпал на первый билет и выпал на второй}, {выигрыш выпал на оба билета}, {на оба билета выигрыш не выпал}. Эти события образуют полную группу попарно несовместных событий.

Пример 1.13. Стрелок произвел выстрел по цели. Обязательно произойдет одно из следующих двух событий: попадание или промах. Эти два несовместных события образуют полную группу.

События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

3. Операции над событиями: сумма (объединение), произведение (пересечение) и разность событий; диаграммы Вьенна.

1.3. Операции над событиями

События обозначаются заглавными буквами начала латинского алфавита A, B, C, D, …, снабжая их при необходимости индексами. Тот факт, что элементарный исход х содержится в событии А, обозначают .

Для понимания удобна геометрическая интерпретация при помощи диаграмм Виенна: представим пространство элементарных событий Ω в виде квадрата, каждой точке которого соответствует элементарное событие. Случайные события А и В, состоящие из совокупности элементарных событий х_i и у_j, соответственно, геометрически изображаются в виде некоторых фигур, лежащих в квадрате Ω (рис. 1-а, 1-б).

Пусть опыт состоит в том, что внутри квадрата, изображенного на рисунке 1-а, выбирается наугад точка. Обозначим через А событие, состоящее в том, что {выбранная точка лежит внутри левой окружности} (рис.1-а), через В – событие, состоящее в том, что {выбранная точка лежит внутри правой окружности} (рис. 1-б).

Достоверному событию благоприятствует любое , поэтому достоверное событие будем обозначать тем же символом Ω.

Два события тождественны друг другу (А=В) тогда и только тогда, когда эти события состоят из одних и тех же элементарных событий (точек).

Суммой (или объединением) двух событий А и В называется событие А+В (или ), происходящее тогда и только тогда, когда происходит или А, или В. Сумме событий А и В соответствует объединение множеств А и В (рис. 1-д).

Пример 1.15. Событие, состоящее в выпадении четного числа, является суммой событий: выпало 2, выпало 4, выпало 6. То есть, {х=четное }= {х=2}+{х=4 }+{х=6 }.

Отметим очевидные соотношения:

Произведением (или пересечением) двух событий А и В называется событие АВ (или ), происходящее тогда и только тогда, когда происходит и А, и В. Произведению событий А и В соответствует пересечение множеств А и В (рис. 1-е).

Пример 1.16. Событие, состоящее в выпадении 5, является пересечением событий: выпало нечетное число и выпало больше 3-х, то есть, A{x=5}=B{x-нечетное}∙C{x>3}.

Отметим очевидные соотношения:

Событие называется противоположным к А, если оно происходит тогда и только тогда, когда А не происходит. Геометрически – это множество точек квадрата, не входящее в подмножество А (рис. 1-в). Аналогично определяется событие (рис. 1-г).

Пример 1.14.. События, состоящие в выпадении четного и нечетного чисел, - события противоположные.

Отметим очевидные соотношения:

Два события называются несовместными, если их одновременное появление в опыте невозможно. Следовательно, если А и В несовместны, то их произведение – невозможное событие:

Введенные ранее элементарные события, очевидно, попарно несовместны, то есть

Пример 1.17. События, состоящие в выпадении четного и нечетного чисел, - события несовместные.

А В а) б) в) г)

А+В АВ или А\В В\А или

д) е) ж) з)

Рис. 1. Диаграммы Виенна

Разностью событий А и В называется событие А\В (или ), происходящее тогда и только тогда, когда происходит А, но не происходит В (рис. 1-ж). Аналогично определяется событие В\А (или (рис.1-з).

Отметим очевидные соотношения: (рис. 1-г).

Так как разность событий можно выразить с помощью операций отрицания и произведения, пользоваться разностью событий в дальнейшем не будем.

Введенные выше операции сложения и умножения обладают следующими свойствами: А+В=В+А, АВ=ВА, А(В+С)=АВ+АС, А(ВС)=(АВ)С.

Пример 1.18. Производится два выстрела по цели. Пусть событие А –{попадание в цель при первом выстреле}, В ––{попадание при втором выстреле}, тогда - промахи, соответственно, при первом и втором выстрелах. Обозначим: событие С –{поражение цели} и примем, что для этого достаточно хотя бы одного попадания. Требуется выразить событие С через события А и В.

Решение. Цель будет поражена в следующих случаях: попадание при первом и промах при втором; промах при первом и попадание при втором; попадание при первом и втором выстрелах. Используя введенные выше операции, перечисленные варианты можно соответственно записать: интересующее нас событие заключается в наступлении или первого, или второго, или третьего вариантов (хотя бы одного), то есть

.

С другой стороны, событие , противоположное событию С, есть промах при двух выстрелах, то есть , отсюда искомое событие С можно записать в виде 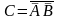. Возможность различного выражения искомого события часто оказывается полезной при решении задач.

4. Относительная частота и вероятность события А. Определение вероятности. Свойства относительной частоты и вероятности. Устойчивость относительной частоты.

Определение вероятности

Ясно, что каждое событие обладает той или иной степенью возможности своего наступления (своей реализации). Чтобы количественно сравнивать между собой события по степени их возможности, очевидно, нужно с каждым событием связать определенное число, которое тем больше, чем более возможно событие. Такое число называется вероятностью события.

Вероятность события – есть численная мера степени объективной возможности наступления этого события.

Рассмотрим стохастический эксперимент и случайное событие А, наблюдаемое в этом эксперименте. Повторим этот эксперимент n раз и пусть m(A) – число экспериментов, в которых событие А произошло.

Отношение (1.1)

называется относительной частотой события А в проведенной серии экспериментов.

Легко убедиться в справедливости свойств:

если А и В несовместны (АВ= ), то ν(А+В) = ν(А) + ν(В) (1.2)

Относительная частота определяется только после проведения серии экспериментов и, вообще говоря, может меняться от серии к серии. Однако опыт показывает, что во многих случаях при увеличении числа опытов относительная частота приближается к некоторому числу. Этот факт устойчивости относительной частоты неоднократно проверялся и может считаться экспериментально установленным.

Пример 1.19.. Если бросить одну монету, никто не сможет предсказать, какой стороной она упадет кверху. Но если бросить две тонны монет, то каждый скажет, что примерно одна тонна упадет кверху гербом, то есть относительная частота выпадения герба примерно равна 0,5.

Если при увеличении числа опытов относительная частота события ν(А) стремится к некоторому фиксированному числу, то говорят, что событие А статистически устойчиво, а это число называют вероятностью события А.

Вероятностью события А называется некоторое фиксированное число Р(А), к которому стремится относительная частота ν(А) этого события при увеличении числа опытов, то есть,

Это определение называют статистическим определением вероятности.

Рассмотрим некий стохастический эксперимент и пусть пространство его элементарных событий состоит из конечного или бесконечного (но счетного) множества элементарных событий ω₁, ω₂, …, ω_i, … . предположим, что каждому элементарному событию ω_i прописан некоторое число - р_i, характеризующее степень возможности появления данного элементарного события и удовлетворяющее следующим свойствам:

(1.3)

Такое число p_i называется вероятностью элементарного события ω_i.

Пусть теперь А- случайное событие, наблюдаемое в этом опыте, и ему соответствует некоторое множество

В такой постановке вероятностью события А называют сумму вероятностей элементарных событий, благоприятствующих А (входящих в соответствующее множество А):

(1.4)

Введенная таким образом вероятность обладает теми же свойствами, что и относительная частота, а именно:

и если АВ= (А и В несовместны),

то P(А+В) = P(А) + P(В)

Действительно, согласно (1.4)

В последнем соотношении мы воспользовались тем, что ни одно элементарное событие не может благоприятствовать одновременно двум несовместным событиям.

Особо отметим, что теория вероятностей не указывает способов определения р_i, их надо искать из соображений практического характера или получать из соответствующего статистического эксперимента.

В качестве примера рассмотрим классическую схему теории вероятностей. Для этого рассмотрим стохастический эксперимент, пространство элементарных событий которого состоит из конечного (n) числа элементов. Предположим дополнительно, что все эти элементарные события равновозможны, то есть вероятности элементарных событий равны p(ω_i)=p_i=p. Отсюда следует, что

Пример 1.20. При бросании симметричной монеты выпадение герба и «решки» равновозможны, их вероятности равны 0,5.

Пример 1.21. При бросании симметричного кубика все грани равновозможны, их вероятности равны 1/6.

Пусть теперь событию А благоприятствует m элементарных событий, их обычно называют исходами, благоприятствующими событию А. Тогда

(1.5)

Получили классическое определение вероятности: вероятность Р(А) события А равна отношению числа исходов, благоприятствующих событию А, к общему числу исходов

Пример 1.22. В урне лежит m белых шаров и n черных. Чему равна вероятность вытащить белый шар?

Решение. Всего элементарных событий m+n. Они все равновероятны. Благоприятствующих событию А из них m. Следовательно, .

Из определения вероятности вытекают следующие ее свойства:

Свойство 1. Вероятность достоверного события равна единице.

Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует собы­тию. В этом случае т=п, следовательно,

P(A)=m/n=n/n=1. (1.6)

Свойство 2. Вероятность невозможного события равна нулю.

Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае т = 0, следовательно, P(A)=m/n=0/n=0. (1.7)

Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испы­тания. То есть, 0≤m≤n, значит, 0≤m/n≤1, следовательно, вероятность любого события удовлетворяет двойному неравенству 0≤P(A) ≤1. (1.8)

Сопоставляя определения вероятности (1.5) и относительной частоты (1.1), заключаем: определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически. Другими словами, вероятность вычисляют до опыта, а относительную частоту - после опыта.

Однако, вычисление вероятности требует наличия предварительной информации о количестве или вероятностях благоприятствующих данному событию элементарных исходов. В случае отсутствия такой предварительной информации для определения вероятности прибегают к эмпирическим данным, то есть, по результатам стохастического эксперимента определяют относительную частоту события.

Пример 1.23. Отдел технического контроля обнаружил 3 нестандартных детали в партии из 80 случайно отобранных деталей. Относительная частота появления нестандартных деталей r (А) = 3/80.

Пример 1.24. По цели .произвели 24 выстрела, причем было зарегистрировано 19 попаданий. Относительная частота поражения цели. r (А) =19/24.

Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Оказалось, что это постоянное число можно принять за приближенное значение вероятности.

Подробнее и точнее связь между относительной частотой и вероятностью будет изложена далее. Теперь же проиллюстрируем свойство устойчивости на примерах.

Пример 1.25. По данным шведской статистики, относительная частота рождения девочек за 1935 г. по месяцам характеризуется сле­дующими числами (числа расположены в порядке следования месяцев, начиная с января): 0,486; 0,489; 0,490; 0.471; 0,478; 0,482; 0.462; 0,484; 0,485; 0,491; 0,482; 0,473

Относительная частота колеблется около числа 0,481, которое можно принять за приближеннее значение вероятности рождения девочек.

Заметим, что статистические данные различных стран дают примерно то же значение относительной частоты.

Пример 1.26. Многократно проводились опыты бросания монеты, в которых подсчитывали число появление «герба». Результаты нескольких опытов приведены в таблице.

Число бросаний	Число появлений «герба»	Относительная частота
4040 12000 24000	2026 5987 12012	0,5016 0,4989 0,5005

Здесь относительные частоты незначительно отклоняются от числа 0,5, причем тем меньше, чем больше число испытаний. Например, при 4040 испытаниях отклонение равно 0,0069, а при 24000 испытаниях - лишь 0,0005. Приняв во внимание, что вероятность появления «герба» при бросании монеты равна 0,5, мы вновь убеждаемся, что относительная частота колеблется около вероятности.

5. Классическое определение вероятности, ограниченность классического определения вероятности. Статистическая вероятность.

Ограниченность классического определения вероятности. Статистическая вероятность

Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же весьма часто встречаются испытания, число возможных исходов которых бесконечно. В таких случаях классическое определение неприменимо. Уже это обстоятельство указывает на ограниченность классического определения. Отмеченный недостаток может быть преодолен, в частности, введением геометрических вероятностей (см. 1.8) и, конечно, использованием аксиоматической вероятности (см. 1.9, замечание).

Наиболее слабая сторона классического определения состоит в том, что очень часто невозможно представить результат испытания в виде совокупности элементарных событий. Еще труднее указать основания, позволяющие считать элементарные события равновозможными. Обычно о равновозможности элементарных исходов испытания говорят из соображений симметрии. Так, например, предполагают, что игральный кубик имеет форму правильного многогранника (куба) и изготовлен из однородного материала. Однако задачи, в которых можно исходить из соображений симметрии, на практике встречаются весьма редко. По этой причине наряду с классическим определением вероятности используют и другие, в частности статистическое определение.

Пусть, в результате проведения n опытов событие А появилось с частотой r(A) = m/n. Практика показывает, что частота события А с увеличением числа опытов n стабилизируется, т.е. стремится к некоторому пределу.

Статистической (эмпирической) вероятностью события А называют число Р(А), к которому стремится частота r(A) события А при неограниченном увеличении числа n опытов, т.е.

Так как на практике неограниченное число опытов невозможно реализовать, в качестве статистической вероятности принимают относительную частоту или число, близкое к ней при достаточно большом числе испытаний. Например, если в результате достаточно большого числа испытаний оказалось, что относительная частота весьма близка к числу 0,4, то это число можно принять за статистическую вероятность события (пример *).

Легко проверить, что свойства вероятности, вытекающие из классического определения (см. 1.3), сохраняются и при статистическом определении вероятности. Действительно:

1) если событие достоверно, то т = п и относительная частота

т/п = n/n = 1,

т. е. статистическая вероятность достоверного события (так же как и в случае классического определения) равна единице.

2) если событие невозможно, то m = 0 и, следовательно, относительная частота 0/n = 0,

т. е. статистическая вероятность невозможного события равна нулю.

3) для любого события 0≤ т ≤ п и, следовательно, относительная частота

0≤ т/п ≤1

т. е. статистическая вероятность любого события заключена между нулем и единицей.

Для существования статистической вероятности события А требуется:

а) возможность, хотя бы принципиально, производить неограниченное число испытаний, в каждом из которых событие А наступает или не наступает;

б) устойчивость относительных частот появления события А в различных сериях достаточно большого числа испытаний.

Недостатком статистической вероятности является неоднозначность статистической вероятности; так, в приведенном примере (*) в качестве вероятности события можно принять не только 0,4, но и 0,39; 0,41 и т. д.

6. Ограниченность классического определения вероятности. Геометрические вероятности

Геометрические вероятности

Чтобы преодолеть недостатки классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов и статистической вероятности – неоднозначность значения вероятности, вводят геометрические вероятности – вероятности попадания точки в некоторую область (отрезок, часть плоскости и т.д.).

Пусть отрезок l составляет часть отрезка L. На отрезок L наугад поставлена точка. Это означает выполнение предположений: поставленная точка с равной вероятностью может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством Р=Длина l/ Длина L.

Пример 1.38. На отрезок ОА длины L числовой оси Ох наугад поставлена точка В(х). Найти вероятность того, что меньший из отрезков ОВ и ВА имеет длину, большую L/3. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения на числовой оси.

Решение. Разобьем отрезок ОА точками С и D на 3 равные части. Требование задачи будет выполнено, если точка В(х) попадет на отрезок CD длины L/3. Искомая вероятность Р=( L/3)/ L = 1/3.

Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наугад брошена точка. Это означает выполнение следующих предположений: брошенная точка с равной вероятностью может оказаться в любой точке фигуры G, вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g. В этих предположениях вероятность попадания точки в фигуру g определяется равенством

Р = Площадь g/ Площадь G.

Пример 1.39. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см, соответственно. Найти вероятность того, что точка, брошенная наугад в большой круг, попадет в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру, пропорциональна площади этой фигуры и не зависит от ее расположения относительно большого круга.

Решение.

П лощадь кольца (фигуры g)

S

Sg

g = π(10²-5²) = 75 π

П лощадь большого круга (фигуры G)

S_G = π10² = 100 π

И

S_G

скомая вероятность

Р = Sg/ S_G =(75 π)/(100π) = 0,75.

Пример 1.40. Ромео и Джульетта договорились встретиться в определенном месте между двенадцатью и часом дня. Необходимо определить вероятность встречи, если приход каждого из них в течение указанного часа происходит случайным образом, причем известно, что Ромео ждет Джульетту ровно 20 минут, а Джульетта Ромео- 5 минут.

Решение. Воспользуемся геометрической схемой вероятности. Обозначим момент прихода Ромео через х, а Джульетты – через у. Тогда любой элементарный исход ω можно отождествить с некоторой точкой на плоскости хОу. Выберем за начало отсчета 12 часов, а за единицу измерения 1 минуту и построим на плоскости хОу пространство элементарных исходов Ω. Очевидно, что это квадрат G со стороной 60.

С обытие А (Ромео и Джульетта встретятся) произойдет тогда, когда разность у-х не превысит t₁ =20, а разность х-у не превысит t₂ =5, т.е. условие встречи определяет систему неравенств у-х ≤ 20;

х-у ≤ 5.

Область элементарных исходов, благоприятствующих событию А представляет заштрихованную область g на рис.

Ее площадь равна площади квадрата без двух угловых треугольников, т.е.

S_G = 60² = 3600

Тогда, согласно определению искомая вероятность равна

Ограниченность классического определения вероятности. Статистическая вероятность

Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же весьма часто встречаются испытания, число возможных исходов которых бесконечно. В таких случаях классическое определение неприменимо. Уже это обстоятельство указывает на ограниченность классического определения. Отмеченный недостаток может быть преодолен, в частности, введением геометрических вероятностей (см. 1.8) и, конечно, использованием аксиоматической вероятности (см. 1.9, замечание).

Наиболее слабая сторона классического определения состоит в том, что очень часто невозможно представить результат испытания в виде совокупности элементарных событий. Еще труднее указать основания, позволяющие считать элементарные события равновозможными. Обычно о равновозможности элементарных исходов испытания говорят из соображений симметрии. Так, например, предполагают, что игральный кубик имеет форму правильного многогранника (куба) и изготовлен из однородного материала. Однако задачи, в которых можно исходить из соображений симметрии, на практике встречаются весьма редко. По этой причине наряду с классическим определением вероятности используют и другие, в частности статистическое определение.

Пусть, в результате проведения n опытов событие А появилось с частотой r(A) = m/n. Практика показывает, что частота события А с увеличением числа опытов n стабилизируется, т.е. стремится к некоторому пределу.

Статистической (эмпирической) вероятностью события А называют число Р(А), к которому стремится частота r(A) события А при неограниченном увеличении числа n опытов, т.е.

Так как на практике неограниченное число опытов невозможно реализовать, в качестве статистической вероятности принимают относительную частоту или число, близкое к ней при достаточно большом числе испытаний. Например, если в результате достаточно большого числа испытаний оказалось, что относительная частота весьма близка к числу 0,4, то это число можно принять за статистическую вероятность события (пример *).

Легко проверить, что свойства вероятности, вытекающие из классического определения (см. 1.3), сохраняются и при статистическом определении вероятности. Действительно:

1) если событие достоверно, то т = п и относительная частота

т/п = n/n = 1,

т. е. статистическая вероятность достоверного события (так же как и в случае классического определения) равна единице.

2) если событие невозможно, то m = 0 и, следовательно, относительная частота 0/n = 0,

т. е. статистическая вероятность невозможного события равна нулю.

3) для любого события 0≤ т ≤ п и, следовательно, относительная частота

0≤ т/п ≤1

т. е. статистическая вероятность любого события заключена между нулем и единицей.

Для существования статистической вероятности события А требуется:

а) возможность, хотя бы принципиально, производить неограниченное число испытаний, в каждом из которых событие А наступает или не наступает;

б) устойчивость относительных частот появления события А в различных сериях достаточно большого числа испытаний.

Недостатком статистической вероятности является неоднозначность статистической вероятности; так, в приведенном примере (*) в качестве вероятности события можно принять не только 0,4, но и 0,39; 0,41 и т. д.

7. Формулы комбинаторики. Размещения и сочетания. Формула Стирлинга.

Формулы комбинаторики.

Для решения задач, связанных с непосредственным вычислением вероятностей, разработана техника подсчета всевозможных комбинаций предметов, в которых используются формулы комбинаторики.

Комбинаторика – раздел математики, посвященный решению задач выбора и расположения элементов некоторого, обычно конечного, множества в соответствии с заданными правилами.

Другими словами, целью комбинаторного анализа является построение некоторой конструкции, называемой комбинаторной конструкцией, подчиненной определенным условиям, которые можно составить из элементов заданного конечного множества независимо от природы этих элементов.

Приведем наиболее употребительные из них

1. Размещениями называют комбинации, составленные из п различных элементов по m элементов, которые от­личаются либо составом элементов, либо их порядком.

Пусть из некоторого множества, состоящего из n различимых элементов, отбирается в определенном порядке m. Для подсчета возможных вариантов заметим, что первый элемент можно выбрать n способами, второй – (n-1) способами, …, m-ый вариант – (n-m+1) способами. Согласно правилу произведения общее число вариантов будет равно n∙(n-1) ∙ … ∙(n-m+1). Такие комбинации называют размещениями, число всех возможных размещений

, (1.9)

где n! = 1∙2∙3∙. . . ∙n (читается n-факториал).

Пример 1.27. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2, если имеет значение цвет флажка в каждой руке?

Решение. Искомое число сигналов

Пример 1.28. Сколькими способами из 20 членов правления фирмы можно отобрать трех для замещения вакансий вице-президентов, отвечающих соответственно за производство, финансы, реализацию продукции?

Решение. Поскольку порядок при таком выборе играет существенную роль, число вариантов равно

2. Перестановками называют комбинации, состоящие из одних и тех же п различных элементов и отличающихся только порядком их расположения.

Число всех возможных перестановок равно числу размещений при n=m, то есть (1.10)

Здесь учтено, что 0! = 0∙1 = 1.

Пример 1.29. Сколько трехзначных чисел можно составить из цифр 1 , 2, 3, если каждая цифра входит в изображение числа только один раз?

Решение. Искомое число трехзначных чисел

Р₃ = 3! = 1∙2∙3 = 6.

Это 1, 2, 3 или 1, 3, 2, или 2, 1, 3, или 2, 3, 1, или 3, 1, 2, или 3, 2, 1.

Если в размещениях порядок отбираемых m элементов из n не играет роли, то говорят о числе сочетаний из n элементов по m.

3. Сочетаниями называют комбинации, составленные из n различных элементов по т элементов, которые отли­чаются хотя бы одним элементом. Число сочетаний

(1.11)

Пример 1.30. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2, если цвет флажка в каждой руке не имеет значения?

Решение. Искомое число сигналов

Пример 1.31. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?

Решение. Искомое число способов

Пример 1.32. Сколькими способами можно из 20 присяжных заседателей отобрать трех для участия в судебном процессе.

Решение. Поскольку несущественно, в каком порядке отобраны кандидатуры, число вариантов равно

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством (1.11-а)

Примечание 1. Выше предполагалось, что все п элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть n₁ элементов одного вида, п₂ элементов другого вида и т. д, то число перестановок с повторениями

P_n(n₁, п₂, … ) = (1.12)

где n₁ + n₂ + . . . = п.

При решении задач комбинаторики используют следующие правила:

Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, другой объект В может быть выбран п способами, то выбрать либо А, либо В можно т + п способами.

Правило произведения. Если объект А можно выбрать из совокупности объектов т способами и после каждого такого выбора объект В можно выбрать п спо­собами, то пара объектов (А, В) в указанном порядке может быть выбрана тп способами.

Примечание 2. При большом n подсчет числа вариантов по приведенным выше формулам требует громоздких вычислений n!. В этом случае пользуются асимптотической формулой Стирлинга

(1.13)

Пример 1.33. Среди K поставленных единиц данного товара S не удовлетворяют предъявляемым условиям. Найти вероятность того, что среди k≤K, отобранных для выборочного контроля качества, равно s≤S не будут удовлетворять этим требованиям (этот опыт называется «контролем качества»).

Решение. Опыт в случайном отборе отборе k образцов. Следовательно, исходы этого испытания равновозможны и общее число вариантов отбора равно . Событие А состоит в том, что из k отобранных ровно s не будут удовлетворять этим требованиям. Число исходов, благоприятствующих А, согласно правилу произведения равно здесь первый множитель дает число вариантов отбора хороших, а второй – плохих образцов. Отсюда искомая вероятность

8. Аксиоматика теории вероятностей: аксиома существования вероятности; вероятность достоверного события; аксиома сложения вероятностей; расширенная аксиома сложения вероятностей.

Аксиоматика теории вероятностей

Предложенное выше классическое определение вероятности наряду с очевидными достоинствами, прежде всего простотой и интуитивной наглядностью, имеет и ряд существенных недостатков: предусматривает только конечное или счетное множество элементарных событий и обязательно знание их вероятностей. Всё это далеко не всегда имеет место, и поэтому введенное определение не является достаточно общим. В настоящее время стало общепринятым аксиоматическое построение теории вероятностей.

В математике аксиомами называются предложения, которые принимаются за истинные и в пределах данной теории не доказываются. Все остальные положения этой теории должны выводится чисто логическим путем из принятых аксиом. Формулировка аксиом представляет собой не начальную стадию развития математической науки, а является результатом длительного накопления фактов и логического анализа полученных результатов с целью выявления действительно основных первичных фактов. Именно так складывались аксиомы геометрии. Подобный же путь прошла и теория вероятностей, в которой аксиоматическое построение ее основ явилось делом сравнительно недавнего прошлого. Впервые задача аксиоматического построения теории вероятностей была решена в 1917 году советским математиком С.Н. Бернштейном.

В настоящее время общепринята аксиоматика академика А.Н. Колмогорова (1933 г.), которая связывает теорию вероятностей с теорией множеств и метрической теорией функций.

В аксиоматике А.Н. Колмогорова первичным является пространство (множество) элементарных исходов Ω. Что представляют собой элементы этого множества для логического развития теории вероятностей – безразлично. Далее рассматривается некоторая система F подмножеств множества Ω; элементы системы F называются случайными событиями. Относительно структуры системы F предполагаются выполненными три следующих требования:

1. Подмножество F в качестве элемента содержит достоверное событие Ω.

2. Если А и В – два события, определенные на Ω, входят в подмножество F в качестве элементов, то в качестве элементов подмножество F также содержит А+В, А∙В,

3. Если события А₁, А₂, …, определенные на Ω, являются элементами подмножества F, то их сумма и произведение также являются элементами подмножества F.

Множество F, образованное описанным выше способом называют «σ-ал-геброй событий».

Теперь перейдем к формулировке аксиом, определяющих вероятность.

Аксиома 1. (аксиома существования вероятности). Каждому случайному событию А из σ-алгебры событий F поставлено в соответствие неотрицательное число р(А), называемое его вероятностью.

Аксиома 2. (вероятность достоверного события). Вероятность достоверного события равна 1: Р(Ω)=1. (1.15)

Аксиома 3. (аксиома сложения). Если события А и В несовместны, то

Р(А+В) = P(А)+Р(В). (1.16)

Аксиома 4. (расширенная аксиома сложения). Если событие А равносильно наступлению хотя бы одного из попарно несовместных событий А₁, А₂, …, то есть, , то вероятность события А равна

(1.17)

Вероятность события Р(А) – численная мера степени объективной возможности этого события, удовлетворяющая вышеуказанным аксиомам.

Первые три аксиомы определяют вероятность.

Необходимость расширенной аксиомы сложения (аксиомы 4) связана с тем, что в теории вероятностей постоянно приходится рассматривать события, подразделяющиеся на бесконечное число частных случаев. Выведем из них несколько следствий, которые в некоторых учебниках представляются теоремами.

9. Некоторые теоремы теории вероятностей: вероятность противоположного события; вероятность появления хотя бы одного события; вероятность суммы двух событий; вероятность суммы двух любых случайных событий.

Некоторые теоремы теории вероятностей

Для задач теории вероятностей наиболее типична ситуация, когда по известным вероятностям одних событий требуется определить вероятность интересующего нас события. Для этого используются теоремы, которые позволяют выразить вероятность одного события через вероятность других.