Решение системы линейных уравнений методом Гаусса сводится к следующему алгоритму:

1. Первым в системе записать уравнение, в котором х₁ отличен от нуля. С помощью элементарных преобразований исключить неизвестное x₁ из всех уравнений, начиная со второго. Для этого а₁₁ должно быть отлично от нуля; необходимо умножать последовательно на 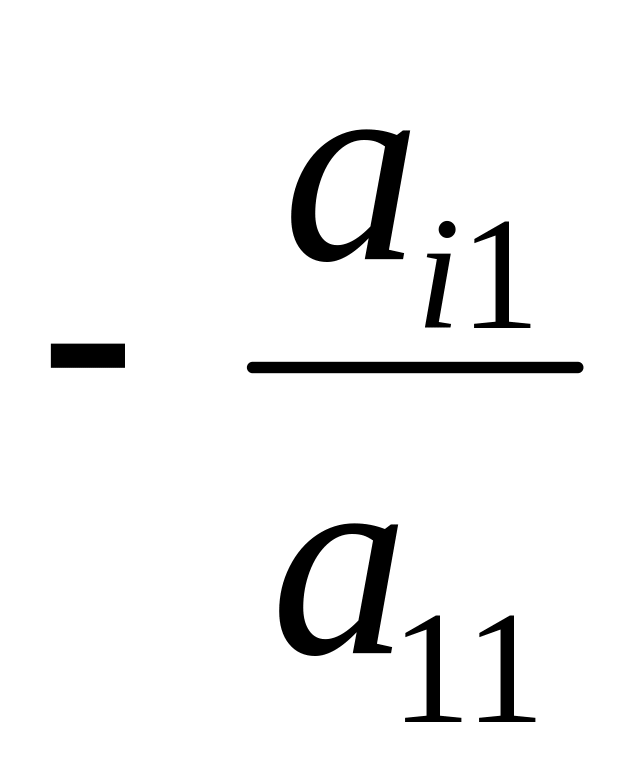первое уравнение и складывать соответственно с i – м уравнением. Получим эквивалентную систему:

,

где и - новые значения коэффициентов и правых частей, которые получаются после проделывания этого шага.

Добиться того, чтобы а₂₂  0. С помощью элементарных преобразований исключаем неизвестное x₂ из всех уравнений, начиная с третьего.

2. И продолжить этот процесс пока это возможно.

3. В результате получить систему ступенчатого (треугольного) вида, которая равносильна исходной. Решение полученной системы будет являться решением исходной системы.

При решении системы уравнений методом Гаусса удобно применять матрицы.

Для этого необходимо выполнить следующее:

1) Записать расширенную матрицу А коэффициентов исходной системы:

2) С помощью элементарных преобразований

привести ее к ступенчатому виду:

.

3) В результате получить систему, решение которой будет являться решением исходной системы.

1.4. Решение систем линейных алгебраических уравнений методом квадратных корней.

Метод квадратных корней используется для решения линейной системы вида АХ = В, у которой матрица А симметрическая, т.е. для элементов выполняется условие a_ij = a_ji (i, j = 1, 2, …, n).

Решение системы таким способом осуществляется в два этапа.

1. Прямой ход.

Представим матрицу А в виде произведения двух взаимно транспонированных треугольных матриц: А = Т Т, где

.

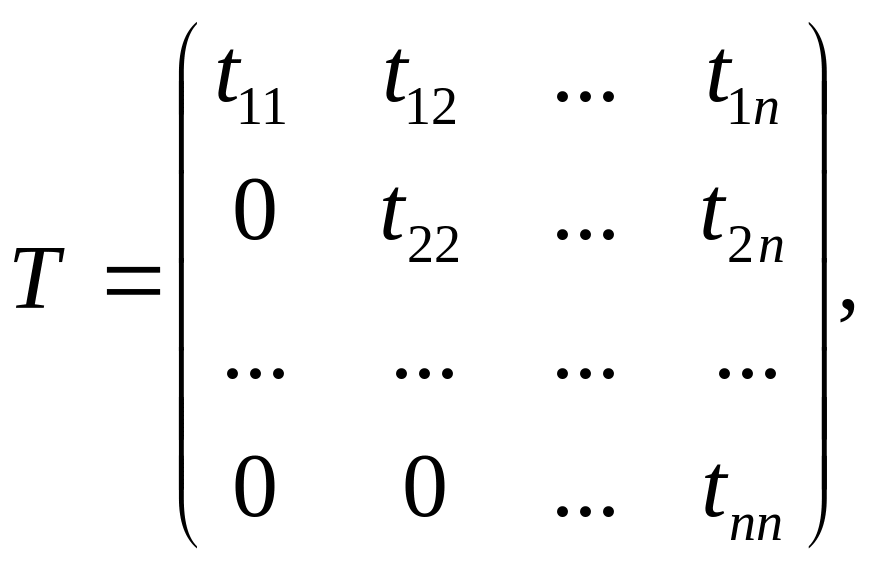
Перемножая матрицы T и T и приравнивая матрице A, получим следующие формулы для определения t_ij:

После того, как матрица Т найдена, систему заменяем двумя эквивалентными ей системами с треугольными матрицами:

Ty = b, Tx = y.

2. Обратный ход.

Записываем в развернутом виде системы:

Отсюда последовательно находим:

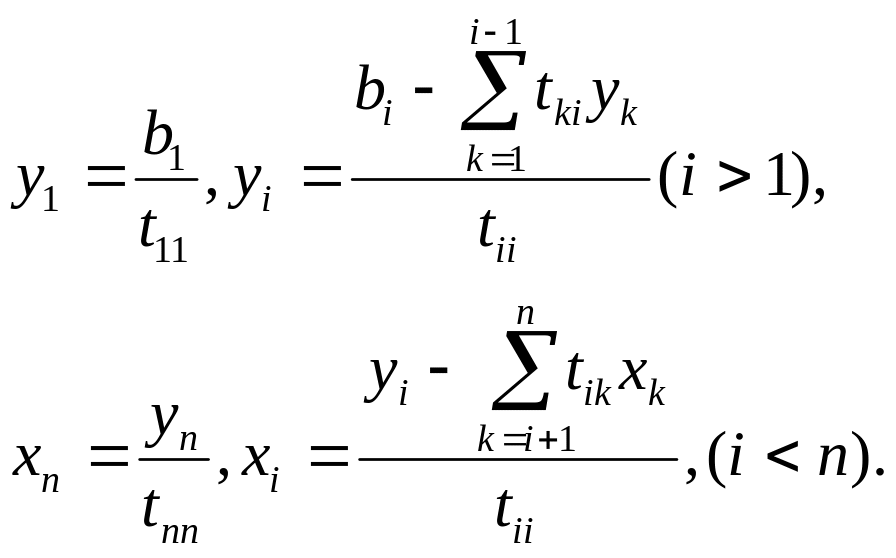
1.5. Решение систем линейных алгебраических уравнений методом обратных матриц.

Пусть дана система из n линейных уравнений с n неизвестными x₁, x₂,…,x_n:

Рассмотрим квадратную матрицу

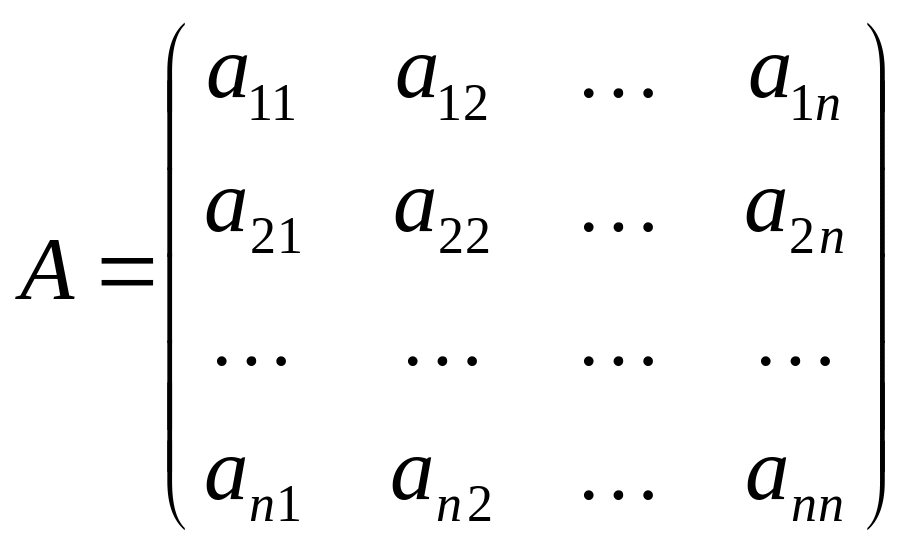
Обозначим  = det A (определитель матрицы А).

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной (или особенной), если  = 0.

Матрица, обратная матрице А, обозначается через А^-1.

Квадратная матрица А^-1 называется обратной для квадратной матрицы А того же порядка, если их произведение А* А^-1 = А^-1*А = Е, где Е ─ единичная матрица того же порядка, что и матрицы А и А^-1.

ТЕОРЕМА. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Обратная матрица вычисляется по формуле:

,

где А_ij ─ алгебраические дополнения элементов a_ij.

А_ij к элементу находим по формуле: A_ij = (-1)^1+jМ .

Минор элемента a_ij – это определитель, полученный из данного определителя вычеркиванием i-ой строки и j-гo столбца.

Если систему уравнений представить в матрич­ном виде: А ∙ X = В,

где А^-1 - обратная матрица к квадратной матрице ,

тогда решение системы уравнений находим по формуле: Х = А^-1 ∙ В .