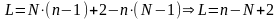- •1. Классификация основных процессов и аппаратов. Классификация процессов по способу создания движущей силы:
- •По способу осуществления различных процессов во времени:
- •Аппараты имеют такую же классификацию, что и процессы:
- •2. Основные признаки массообменных процессов.
- •3. Основное уравнение массопередачи.
- •4. Материальный баланс массообменного процесса.
- •Уравнения расхода фаз
- •5. Рабочая линия.
- •Уравнение линии концентраций (рабочей линии, оперативной линии)
- •6. Графическое представление массообменного процессса.
- •7. Движущая сила массообменных процессов.
- •8. Средняя интегральная движущая сила.
- •9. Средняя логарифмическая движущая сила.
- •10,11. Число единиц переноса (чеп).
- •13. Способы выражения составов фаз.
- •12. Теоретическая тарелка, вэтт.
- •14. Правило фаз Гиббса.
- •15. Насыщенные и ненасыщенные пары.
- •16. Классификация бинарных смесей.
- •17. Основные законы фазового равновесия.
- •18, Равновесие идеальных бинарных смесей, изотерма жидкой фазы.
- •19. Равновесие идеальных бинарных смесей, изотерма паровой фазы
- •2 0. Графический расчет равновесных составов паров и жидкости.
- •21. Кривая равновесия фаз.
- •22. Изобарно-температурные кривые
- •2 3.Энтальпийная диаграмма
- •24. Равновесие бинарных смесей, частично отклоняющихся от закона Рауля; коэффициент активности
- •25. Равновнсие взаимно растворимых бинарных смесей, образующих азеотропные смеси
- •26. Равновесие частично растворимых жидкостей; гетероазеотропы
- •27. Равновесие взаимно нерастворимых жидкостей.
- •28. Способы перегонки жидкостей
- •Постепенное испарение
- •29.Расчет процесса ои. Мат и тепло балансы процесса
- •30. Постепенное испарение
- •31.Постепенная конденсация
- •32.Многократное испарение
- •3 3.Многократная конденсация
- •34.Сущность процесса ректификации
- •3 5. Принципиальное устройство ректификационной колонны
- •36.Материальный баланс ректификационной колонны
- •3 7.Расчет минимальных флегмовых и паровых
- •3 8.Уравнение рабочей линии верхней части колонны
- •39.Уравнение рабочей линии для нижней части колонны
- •40.Внутреннее и внешнее флегмовое число
- •41.Тепловой баланс колонны
- •42.Тепловой баланс для верхней части колонны
- •43.Тепловой баланс для нижней части колонны
- •44. Построение рабочих линий на диаграмме X-y при помощи энтальпийной диаграмме (эд)
- •45.Режим полного орошения
- •46. Режим минимального орошения.
- •47. Графическое определение числа теоретических тарелок на диаграмме х-y
- •48. Графическое определение числа теоретических тарелок при помощи энтальпийной диаграммы и изобарных температурных кривых.
- •51.Холодное (острое)испаряющееся орошение
- •52.Циркуляционное орошение
- •5 3.Способы подвода тепла в низ колонны
- •54.Выбор давления при ректификации
- •55.Особенности работы колонны с вводом водяного пара
- •56. . Способы расчета числа единиц переноса.
- •1Й способ:
- •2Ой способ:
- •57.60. Расчет ректификации многокомпонентных смесей в режиме полного орошения. Уравнение Фенске
- •58.59 Расчет ректификации многокомпонентных смесей в режиме минимального орошения. Уравнение Андервуда
8. Средняя интегральная движущая сила.
Средняя движущая сила определяет количество переданной массы вещества. Т.к рабочие и равновесные концентрации изменяются вдоль поверхности контакта фаз, то нужно рассчитывать среднюю движущую силу процесса.
Допустим
что рабочая и равновесная линия – кривые
или раб.линия–прямая, а равн.линия –
кривая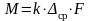 (1) – основное уравнение массопередачи
(1) – основное уравнение массопередачи
из
(1) получаем:
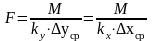 (2) ; где F-
поверхность фазового контакта
(2) ; где F-
поверхность фазового контакта
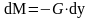 (3)
- диф.уравнение мат.баланса фазы G
(3)
- диф.уравнение мат.баланса фазы G
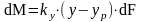 (4) – уравнение массоопередачи из (3) и
(4)
(4) – уравнение массоопередачи из (3) и
(4)
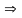
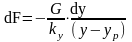 (5)
(5)
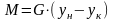 (6)
(6)
подставив (6) в (5)
 (7)
проинтегрировав выражение (7)
(7)
проинтегрировав выражение (7)
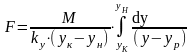 (8)подставив
выражение (2)
(8)подставив
выражение (2)
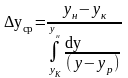 - средняя интегральная разность
концентраций для газовой фазы
- средняя интегральная разность
концентраций для газовой фазы
Аналогично
выводится выражение для жидкой фазы:
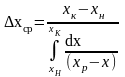
9. Средняя логарифмическая движущая сила.

Допустим,
что равновесная и рабочая линии являются
прямыми.
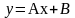 (1) – уравнение рабочей линии
(1) – уравнение рабочей линии
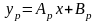 (2)
– уравнение равновесия
(2)
– уравнение равновесия
 (3)
– разность рабочей и равновесной
концентрации
(3)
– разность рабочей и равновесной
концентрации
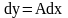 (4) проинтегрируем урав (3) с учетом (4) →
(4) проинтегрируем урав (3) с учетом (4) →
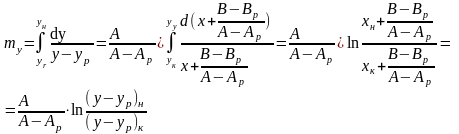 (5) →
(5) →
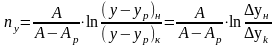 (6)
(6)
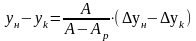 (7)
(8) – СИРК
(7)
(8) – СИРК
подставим
урав (8) и (7) в урав (6) →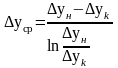 - СЛРК для газовой фазы. Аналогично
выводится выражение для жидкой фазы:
- СЛРК для газовой фазы. Аналогично
выводится выражение для жидкой фазы:
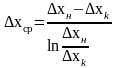
10,11. Число единиц переноса (чеп).
Показывает, сколько единиц вещества переходит в другую фазу при движущей силе, равной единице.
 ЧЕП
используют для расчета массообменного
аппарата.
ЧЕП
используют для расчета массообменного
аппарата.
и - СИРК для газовой и жидкой фаз. →

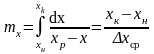 -
ЧЕП для паровой и жидкой фазы; где
-
ЧЕП для паровой и жидкой фазы; где
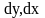 -
изменение концентрации в фазе G,L
в результате массообмена фаз на
поверхности
-
изменение концентрации в фазе G,L
в результате массообмена фаз на
поверхности
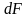 ,
,
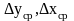 -
движущая сила на этой поверхности.
-
движущая сила на этой поверхности.
13. Способы выражения составов фаз.
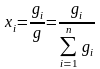
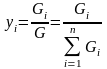 (1)
- массовые
доли
компонентов в жидкой (
(1)
- массовые
доли
компонентов в жидкой (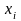 )
и паровой фазе
)
и паровой фазе
( );
где g
и G-
массы жидкой и паровой фаз,
);
где g
и G-
массы жидкой и паровой фаз,
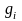 и
и
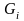 -компонент
жид/пар.фазы.
-компонент
жид/пар.фазы.
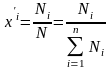
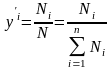 (2)
- мольные
доли
компонентов в жидкой (
(2)
- мольные
доли
компонентов в жидкой (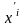 )
и паровой фазе (
)
и паровой фазе (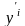 );
где
);
где
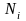 -число
молей компонента и N-общее
число молей смеси.
-число
молей компонента и N-общее
число молей смеси.
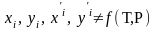
 (3)
- объемная
доля компонента;
где
(3)
- объемная
доля компонента;
где
 -объем
компонента и V-общий
объем.
-объем
компонента и V-общий
объем.
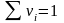 ,
,
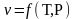
Пересчет массовых и мольных долей:

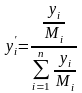 -
переход из мольных в массовые доли.
-
переход из мольных в массовые доли.
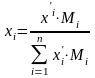
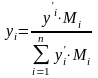 -
переход из массовых в мольные доли.
-
переход из массовых в мольные доли.

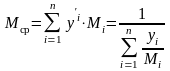 -
средняя
мольная/массовая масса
смеси.
-
средняя
мольная/массовая масса
смеси.
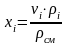 -
пересчет массовой доли в объемную.
-
пересчет массовой доли в объемную.
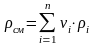 -
средняя
плотность смеси.
-
средняя
плотность смеси.
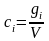 -
объемная
концентрация.
-
объемная
концентрация.
12. Теоретическая тарелка, вэтт.
Теоретическая
тарелка
– контакт массобменивающихся фаз,
который приводит систему в состояние
равновесия. ЧТТ может быть рассчитано
аналитическим или графическим методом
при совместном решении уравнений
равновесия и рабочей линии процесса.
Одна теоретическая тарелка выражает
одно изменение движущей силы по газовой
Δy и одно изменение по жидкой Δx фазам.
ЧТТ
и движущая сила процесса находятся в
обратном соотношении.


ЧТТ используется для определения высоты контактной зоны аппарата Н, для этого используют ВЭТТ.
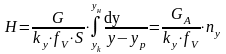 – высота
аппарата, где H,
S
–высота и сечение ап-та, G
–расход ф.G
[кг/с],
– высота
аппарата, где H,
S
–высота и сечение ап-та, G
–расход ф.G
[кг/с],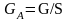 -массовая
скорость ф. G
-массовая
скорость ф. G
[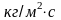 ]
]
из
урав →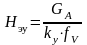 - высота, эквивалентная одной единице
переноса.
- высота, эквивалентная одной единице
переноса.
14. Правило фаз Гиббса.
Состояние равновесия характеризуется правилом фаз Гиббса, которое определяет связь между числом степеней свободы, числом ее компонентов и числом фаз.
Число независимых параметров, которые могут быть выбраны произвольно, чтобы привести систему в состояние равновесия – число степеней свободы.
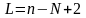 где
L
– число степеней свободы n
– число компонентов N
– число фаз.
где
L
– число степеней свободы n
– число компонентов N
– число фаз.
В качестве степеней свободы могут выступать t,P,c
Для 2-х компонентной системы взаимно растворимых жидкостей L=2, а для нерастворимых L=1
Вывод уравнения:
1) Пусть система содержит N фаз и n компонентов в каждой фазе.
2) Состояние фаз фиксировано при Р и Т.
3)
Состав каждой фазы можно рассчитать,
задавая n-1
концентраций компонентов, а концентрация
одного из компонентов является зависимой
величиной и может быть рассчитана из
условия, что сумма мольных долей всех
компонентов в смеси равна 1.
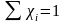
4)
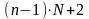 - общее число переменных, определяющих
состояние системы.
- общее число переменных, определяющих
состояние системы.
5)
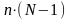 -
общее число уравнений для расчета
состояния системы, где (N-1)
– число уравнений, достаточных для
расчета концентрации компонентов, n
– число переменных.
-
общее число уравнений для расчета
состояния системы, где (N-1)
– число уравнений, достаточных для
расчета концентрации компонентов, n
– число переменных.
6) Число уравнений не может превышать числа переменных, иначе уравнения будут несовместимыми. Разность между числом независимых переменных и числом уравнений равна числу произвольно изменяемых параметров в данной системе, меняя которые можно не менять число фаз в ней (степень свободы):