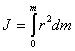19. Движение центра масс твердого тела

Представим твердое тело как систему материальных точек, разбив его на элементарные массы . Каждая масса может находиться под воздействием внутренних сил и внешних . По второму закону Ньютона .

Сложив эти уравнения для всех частиц тела, получаем

.

Сумма всех внутренних сил, действующих в системе, равна нулю, тогда

.

Сумму, стоящую в левой части, можно заменить произведением массы системы на ускорение центра масс , поэтому

.

- центр масс (инерции) твердого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием всех приложенных к телу сил, на ускорение центра масс (см. главу 2).

 

20. Вращение твердого тела вокруг неподвижной оси

Вращением твер­дого тела вокруг неподвижной оси называется такое движение, при котором все его точки, лежащие на некоторой прямой, называемой осью вращения, все время остаются неподвижными.

Рассмотрим вращение твердого тела (рис. 2.11) вокруг оси, проходящей через две неподвижные точки    и  . Проведем через ось    неподвижную полуплоскость    и движущуюся вместе с телом полуплоскость  . Вращение тела будет определяться величиной дву­г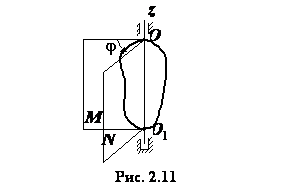 ранного угла    между по-луплоскостями    и  . Угол    называется углом поворота. Условимся считать за положительное направление вращения тот случай, когда, смотря с заданного направления оси вращения, увеличение угла поворота наблюдается в сторону, противоположную движению часовой стрелки.

При вращении угол поворота    изменяется в зависимости от времени. Равенство:

  

является уравнением вращения тела вокруг неподвижной оси. Оно позволяет определить положение тела в любой момент времени. Угол    в равенстве (2.30) выражается в радианах.

21. Момент инерции.

Чтобы найти момент инерции тела, надо просуммировать момент инерции всех материальных точек, составляющих данное тело

В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами , и моменты инерции тела определяется интегралом

о где - расстояние от элемента до оси вращения.

Распределение массы в пределах тела можно охарактеризовать с помощью плотности

где m - масса однородного тела, V - его объем. Для тела с неравномерно распределенной массой это выражение даетсреднюю плотность.

Плотность в данной точке в этом случае определяется следующим образом

и тогда

Пределы интегрирования зависят от формы и размеров тела Интегрирование уравнения (5.5) наиболее просто осуществить для тех случаев, когда ось вращения проходит через центр тяжести тела. Рассмотрим результаты интегрирования для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.

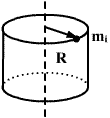
Момент инерции полого цилиндра с тонкими стенками, радиуса R.

Для полого цилиндра с тонкими стенками

Сплошной однородный диск. Ось вращения является осью диска радиуса . и массы m с плотностью Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки и массой . Для него

Весь диск можно разбить на бесконечное множество цилиндров, а затем просуммировать:

Момент инерции шара относительно оси, проходящей через центр тяжести.

Момент инерции стержня длиной L и массой m относительно оси, проходящей:

а) через центр стержня -

б) через начало стержня -

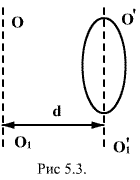
Теорема Штейнера. Имеем тело, момент инерции которого относительно оси, проходящей через его центр масс известен. Необходимо определить момент инерции относительно произвольно оси параллельной оси . Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями: