
- •2. Скорость
- •3. Ускорение
- •4.Кинематика вращательного движения.
- •5. Сила. Масса тела и импульс
- •6. Принцип относительности Галилея
- •8. Силы трения
- •9. Сила тяжести. Вес.
- •10. Работа. Мощность. Кинетическая энергия.
- •14. Условия равновесия механической системы.
- •15. Закон сохранения импульса
- •16. Закон сохранения момента импульса
- •17. Силы инерции
- •18. Центробежная сила инерции. Сила Кориолиса.
- •19. Движение центра масс твердого тела
- •20. Вращение твердого тела вокруг неподвижной оси
- •21. Момент инерции.
- •22. Кинетическая энергия вращающегося твердого тела
- •23. Гироскопы.
- •24. Гармонические колебания
- •25. Маятники
- •26. Энергия гармонического осциллятора
- •27. Сложение колебаний одного направления.Биения.
- •28. Затухающие колебания
- •29. Вынужденные колебания
- •30. Линии и трубки тока. Неразрывность струи
- •31. Уравнение Бернулли для стационарного течения несжимаемой жидкости
- •32. Силы внутреннего трения.Формула Стокса.
- •33. Давление газа
- •34.Температура.
- •35. Уравнение состояния идеального газа.
- •36. Внутренняя энергия идеального газа. Количество теплоты.
- •37. Первое начало термодинамики
- •38. Теплоёмкость идеального газа
- •39. Работа, совершаемая газом при различных процессах
- •40. Термодинамические процессы
- •42. Холодильные машины
- •43. Поверхностное натяжение
- •44. Капиллярные явления
10. Работа. Мощность. Кинетическая энергия.
Работа.
Изменение механического движения и энергии тела происходит в процессе силового взаимодействия этого тела с другими телами. Для количественной характеристики этого процесса в механике вводят понятие работы, совершаемой силой.
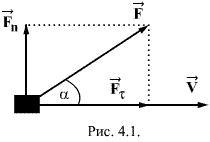
Если
рассматриваемая сила
![]() постоянна,а
тело, к которому она приложена, движется
поступательно и прямолинейно, то работой,
совершаемой силой
постоянна,а
тело, к которому она приложена, движется
поступательно и прямолинейно, то работой,
совершаемой силой
![]() при
прохождении телом пути
при
прохождении телом пути
![]() ,
называют величину
,
называют величину
|
(4.1) |
где а - угол между силой и направлением движения тела.
Работа
- скалярная величина. Если вектор силы
и вектор перемещений образуют острый
угол т.е.
![]() ,
то
,
то
![]() ,
если
,
если
![]() ,
то
,
то
![]() ,
т.е. сила, действующая перпендикулярно
к перемещению тела, работы не совершает.
,
т.е. сила, действующая перпендикулярно
к перемещению тела, работы не совершает.
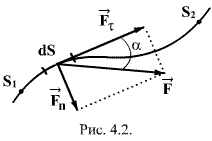
В
общем случае тело может двигаться
произвольным, достаточно сложным образом
(рис.4.2). Выделим элементарный участок
пути
![]() ,
на котором силу можно считать постоянной
и перемещение прямолинейным. Элементарная
работа на этом участке равна
,
на котором силу можно считать постоянной
и перемещение прямолинейным. Элементарная
работа на этом участке равна
|
(4.2) |
Полная
работа на пути
![]() определяется
интегралом
определяется
интегралом
Мощность Величина,
характеризующая скорость совершения
работы, называется мощностью Мощность
численно равна отношению
или в общем случае
Подставляя
значение
Кинетическая энергия. Рассмотрим случай, когда материальная точка движется из точки 1 в точку 2 под действием приложенных к ней сил (рис.4.4.)
Причем силы, действующие на материальную точку, могут иметь разную природу, т.е. могут быть консервативными и неконсервативными. Уравнение движения в этом случае запишется в виде
где
Умножим скалярно уравнение (4.7) на и проинтегрируем от точки1 до точки 2, получим:
Учитываем
то, что
величина
называется кинетической энергией материальной точки. Таким образом, кинетическая энергия материальной точки – это энергия, которой обладает эта точка вследствие своего движения. Из полученного выражения (4.9) следует, что работа всех сил, действующих на материальную точку на участке траектории 1-2 равна изменению ее кинетической энергии на этом участке.
11. Потенциальная энергия Потенциальная
энергия - это энергия, обусловленная
взаимным расположением тел и характером
их взаимодействия. При соответствующих
условиях возможно изменение потенциальной
энергии, за счет чего совершается
работа. Для поднятия тела массой m на
высоту
знак минус перед интегралом, т.к. сила Р направлена в сторону противоположную изменению h. Проинтегрируем это выражение:
Эта энергия пойдет на увеличение энергии замкнутой системы тело-Земля т.е. численно равна
Считая
поверхности Земли
Эта
энергия
12. Закон сохранения энергии Рассмотрим процесс изменения состояния тела, поднятого на высоту h. При этом его потенциальная энергия
Тело
начало свободно падать
Кинетическая энергия тела, упавшего с высоты h, оказалась равной его потенциальной энергии, которую оно имело до начала падения. Следовательно:
На
поверхности Земли h=0 и потенциальная
энергия
Потенциальная энергия - уменьшается, и, следовательно, ее изменение имеет знак минус. Поэтому можем записать:
Сложив (4.12) и (4.13), получим
или
Сумма
Таким образом, энергия замкнутой консервативной системы остается постоянной при всех, происходящих в ней процессах и превращениях. Энергия может переходить из одних видов в другие (механические, тепловые, и т.д.), но общее ее количество остается постоянным. Данное положение называют законом сохранения и превращения энергии.
13. Потенциальная энергия деформации
Деформированное упругое тело (например, растянутая или сжатая пружина) способно, возвращаясь в недеформированное состояние, совершить работу над соприкасающимися с ним телами. Следовательно, упруго деформированное тело обладает потенциальной энергией. Она зависит от взаимного положения частей тела, например витков пружины. Работа, которую может совершить растянутая пружина, зависит от начального и конечного растяжений пружины. Найдем работу, которую может совершить растянутая пружина, возвращаясь к нерастянутому состоянию, т. е. найдем потенциальную энергию растянутой пружины. Пусть
растянутая пружина закреплена одним
концом, а второй конец, перемещаясь,
совершает работу. Нужно учитывать,
что сила, с которой действует пружина,
не остается постоянной, а изменяется
пропорционально растяжению. Если
первоначальное растяжение пружины,
считая от нерастянутого состояния,
равнялось
Таким образом, потенциальная энергия растянутой пружины
Такое же выражение получается для сжатой пружины. В
формуле (98.1) потенциальная энергия
выражена через жесткость пружины и
через ее растяжение
.
Заменив
на
которое определяет потенциальную энергию пружины, растянутой (или сжатой) силой . Из этой формулы видно, что, растягивая с одной и той же силой разные пружины, мы сообщим им различный запас потенциальной энергии: чем жестче пружина, т.е. чем больше ее упругость, тем меньше потенциальная энергия; и наоборот: чем мягче пружина, тем больше энергия, которую она запасет при данной растягивающей, силе. Это можно уяснить себе наглядно, если учесть, что при одинаковых действующих силах растяжение мягкой пружины больше, чем жесткой, а потому больше и произведение силы на перемещение точки приложения силы, т. е. работа. Эта закономерность имеет большое значение, например, при устройстве различных рессор и амортизаторов: при посадке на землю самолета амортизатор шасси, сжимаясь, должен произвести большую работу, гася вертикальную скорость самолета. В амортизаторе с малой жесткостью сжатие будет больше, зато возникающие силы упругости будут меньше и самолет будет лучше предохранен от повреждений. По той же причине при тугой накачке шин велосипеда дорожные толчки ощущаются резче, чем при слабой накачке. |
(4.3) |


