
- •2. Скорость
- •3. Ускорение
- •4.Кинематика вращательного движения.
- •5. Сила. Масса тела и импульс
- •6. Принцип относительности Галилея
- •8. Силы трения
- •9. Сила тяжести. Вес.
- •10. Работа. Мощность. Кинетическая энергия.
- •14. Условия равновесия механической системы.
- •15. Закон сохранения импульса
- •16. Закон сохранения момента импульса
- •17. Силы инерции
- •18. Центробежная сила инерции. Сила Кориолиса.
- •19. Движение центра масс твердого тела
- •20. Вращение твердого тела вокруг неподвижной оси
- •21. Момент инерции.
- •22. Кинетическая энергия вращающегося твердого тела
- •23. Гироскопы.
- •24. Гармонические колебания
- •25. Маятники
- •26. Энергия гармонического осциллятора
- •27. Сложение колебаний одного направления.Биения.
- •28. Затухающие колебания
- •29. Вынужденные колебания
- •30. Линии и трубки тока. Неразрывность струи
- •31. Уравнение Бернулли для стационарного течения несжимаемой жидкости
- •32. Силы внутреннего трения.Формула Стокса.
- •33. Давление газа
- •34.Температура.
- •35. Уравнение состояния идеального газа.
- •36. Внутренняя энергия идеального газа. Количество теплоты.
- •37. Первое начало термодинамики
- •38. Теплоёмкость идеального газа
- •39. Работа, совершаемая газом при различных процессах
- •40. Термодинамические процессы
- •42. Холодильные машины
- •43. Поверхностное натяжение
- •44. Капиллярные явления
27. Сложение колебаний одного направления.Биения.
Сложение гармонических колебаний, направленных вдоль одной прямой.
Рассмотрим сложение одинаково направленных колебаний одного периода, но отличающихся начальной фазой и амплитудой. Уравнения складываемых колебаний заданы в следующем виде:
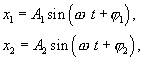
где
![]() и
и
![]() -
смещения;
-
смещения;
![]() и
и
![]() -
амплитуды;
-
амплитуды;
![]() и
и
![]() -
начальные фазы складываемых колебаний.
Амплитуду результирующего колебания
удобно определить с помощью векторной
диаграммы , на которой отложены векторы
амплитуд
-
начальные фазы складываемых колебаний.
Амплитуду результирующего колебания
удобно определить с помощью векторной
диаграммы , на которой отложены векторы
амплитуд
![]() и
и
![]() складываемых
колебаний под углами
и
к
оси х и по правилу параллелограмма
получен вектор амплитуды суммарного
колебания
складываемых
колебаний под углами
и
к
оси х и по правилу параллелограмма
получен вектор амплитуды суммарного
колебания
![]() .
Если равномерно вращать систему векторов
(параллелограмм) и проектировать векторы
на ось OY, то их проекции будут совершать
гармонические колебания в соответствии
с заданными уравнениями. Взаимное
расположение векторов
,
и
при
этом остается неизменным, поэтому
колебательное движение проекции
результирующего вектора
тоже
будет гармоническим.
.
Если равномерно вращать систему векторов
(параллелограмм) и проектировать векторы
на ось OY, то их проекции будут совершать
гармонические колебания в соответствии
с заданными уравнениями. Взаимное
расположение векторов
,
и
при
этом остается неизменным, поэтому
колебательное движение проекции
результирующего вектора
тоже
будет гармоническим.

Отсюда
следует вывод, что суммарное движение
- гармоническое колебание, имеющее
заданную циклическую частоту. Определим
модуль амплитуды А результирующего
колебания В
![]() угол
угол
![]() (из
равенства противоположных углов
параллелограмма).
(из
равенства противоположных углов
параллелограмма).
Следовательно
![]() отсюда
отсюда
![]() .
Согласно
теореме косинусов
.
Согласно
теореме косинусов
![]() или
или
|
|
Начальная
фаза
![]() результирующего
колебания определяется из
результирующего
колебания определяется из
![]() :
:
![]()
Соотношения для фазы и амплитуды позволяют найти амплитуду и начальную фазу результирующего движения и составить его уравнение
![]() Биения
Биения
Рассмотрим
случай, когда частоты двух складываемых
колебаний мало отличаются друг от друга
![]() ,
и пусть амплитуды одинаковы и начальные
фазы
,
и пусть амплитуды одинаковы и начальные
фазы
![]() ,
т.е.
,
т.е.
![]() Сложим
эти уравнения аналитически
Сложим
эти уравнения аналитически
![]()
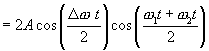 Преобразуем
Преобразуем
![]()
![]() Тогда
Тогда

Так
как
![]() все
же медленно изменяется, величину
все
же медленно изменяется, величину
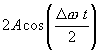 нельзя
назвать амплитудой в полном смысле
этого слова (амплитуда величина
постоянная). Условно эту величину можно
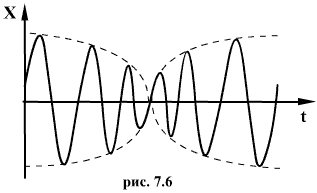
назвать переменной амплитудой. График
таких колебаний показан на рис. 1.6
Складываемые колебания имеют одинаковые
амплитуды, но различны периоды, при этом
периоды
нельзя
назвать амплитудой в полном смысле
этого слова (амплитуда величина
постоянная). Условно эту величину можно
назвать переменной амплитудой. График
таких колебаний показан на рис. 1.6
Складываемые колебания имеют одинаковые
амплитуды, но различны периоды, при этом
периоды
![]() отличаются
незначительно друг от друга. При сложении
таких колебаний наблюдаются биения.
Число n биений в секунду определяется
разностью частот складываемых колебаний,
т.е.
отличаются
незначительно друг от друга. При сложении
таких колебаний наблюдаются биения.
Число n биений в секунду определяется
разностью частот складываемых колебаний,
т.е.
![]()
Биения можно наблюдать при звучании двух камертонов, если частоты и колебаний близки друг к другу.
Сложение взаимно перпендикулярных колебаний.
Пусть материальная точка одновременно участвует в двух гармонических колебаниях, совершающихся с одинаковыми периодами Т в двух взаимно перпендикулярных направлениях. С этими направлениями можно связать прямоугольную систему координат XOY, расположив начало координат в положении равновесия точки. Обозначим смещение точки С вдоль осей ОХ и OY, соответственно, через х и у.
Рассмотрим несколько частных случаев.
A. Начальные фазы колебаний одинаковы. Выберем момент начала отсчета времени таким образом, чтобы начальные фазы обоих колебаний были равны нулю. Тогда смещения вдоль осей ОХ и OY можно выразить уравнениями:
![]() Поделив
почленно эти равенства, получим уравнения
траектории точки С:
Поделив
почленно эти равенства, получим уравнения
траектории точки С:
![]() или
или
![]()
![]()
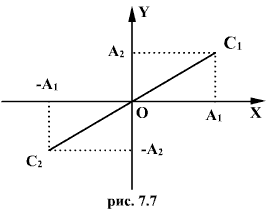
Следовательно,
в результате сложения двух взаимно
перпендикулярных колебаний точка С
колеблется вдоль отрезка
![]() прямой,
проходящей через начало координат.
прямой,
проходящей через начало координат.
Б. Начальная разность фаз равна π Уравнения колебания в этом случае имеют вид:
![]()
Уравнение траектории точки
|
|
Следовательно, точка С колеблется вдоль отрезка прямой, проходящей через начало координат, но лежащие в других квадрантах, чем в первом случае. Амплитуда А результирующих колебаний в обоих рассмотренных случаях равна
![]()
В.
Начальная разность фаз равна
![]() .
.
Уравнения
колебаний имеют вид:
![]() Разделим
первое уравнение на
,
второе - на
:
Разделим
первое уравнение на
,
второе - на
:
![]()
Возведем оба равенства в квадрат и сложим. Получим следующее уравнение траектории результирующего движения колеблющейся точки
|
|
Колеблющаяся
точка С движется по эллипсу с полуосями
и
.
При равных амплитудах
![]() траекторией
суммарного движения будет окружность
траекторией
суммарного движения будет окружность
![]() В
общем случае при
В
общем случае при
![]() ,
но кратным, т.е.
,
но кратным, т.е.
![]() ,
при сложении, взаимно перпендикулярных
колебаний колеблющаяся точка движется
по кривым, называемым фигурами Лиссажу.
Конфигурация этих кривых зависит от
соотношения амплитуд, начальных фаз и
периодов составляющих колебаний.
,
при сложении, взаимно перпендикулярных
колебаний колеблющаяся точка движется
по кривым, называемым фигурами Лиссажу.
Конфигурация этих кривых зависит от
соотношения амплитуд, начальных фаз и
периодов составляющих колебаний.
