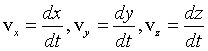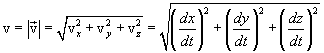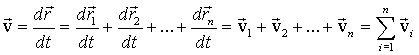1. МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ

Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени.

Механическое движение тел изучает механика. Раздел механики, описывающий геометрические свойства движения без учета масс тел и действующих сил, называется кинематикой.

Путь и перемещение. Линия, по которой движется точка тела, называется траекторией движения. Длина траектории называется пройденным путем. Вектор, соединяющий начальную и конечную точки траектории, называется перемещением.

Движение тела, при котором все его точки в данный момент времени движутся одинаково, называется поступательным движением. Для описания поступательного движения тела достаточно выбрать одну точку и описать ее движение (рис. 1).

Рис. 1

Движение, при котором траектории всех точек тела являются окружностями с центрами на одной прямой и все плоскости окружностей перпендикулярны этой прямой, называется вращательным движением (рис. 2).

Рис. 2

Поступательное и вращательное движения - самые простые примеры механического, движения тел.

При движении автомобиля по дороге его кузов движется поступательно, а колеса совершают вращательное движение относительно осей.

Материальная точка. Тело, размерами которого в данных условиях движения можно пренебречь, называют материальной точкой.

Тело можно рассматривать как материальную точку, если его размеры малы по сравнению с расстоянием, которое оно проходит, или по сравнению с расстояниями от него до других тел. Космический корабль, пролетающий 8 км за 1 с, при наблюдении с поверхности Земли вполне можно рассматривать как материальную точку. Но космонавт, находящийся в космическом корабле, не может считать свой корабль материальной точкой.

Когда траекторией движения материальной точки является прямая линия и направление движения не изменяется, модуль вектора перемещения равен пройденному пути. Если точка движется по криволинейной траектории, то модуль вектора перемещения меньше пройденного пути (рис. 3).

Рис. 3

Если в конкретных условиях тело можно рассматривать как материальную точку, мы будем говорить о координатах тела и траектории движения тела.

Метр. Для определения координат тела необходимо уметь измерять расстояние на прямой между двумя точками. Любой процесс измерения физической величины заключается в сравнении измеряемой величины с единицей измерения этой величины. Единица для измерения длины может быть выбрана произвольно, но для удобства в науке и технике, в торговле и в быту в настоящее время условились во всех странах пользоваться одной единицей длины - метром.

Эталон единицы длины - метр - изготовлен из очень прочного сплава иридия и платины.

Метр равен примерно 1/40000000 части земного меридиана.

По современному определению метр - это расстояние, которое свет проходит в пустоте за 1/299792458 долю секунды. Таким образом, современное определение единицы расстояния связано с определением единицы измерения времени - секундой.

Секунда. Для измерения времени выбирается какой-либо природный периодический процесс или процесс, регулярно повторяющийся в специально изготовленном приборе - часах.

До недавнего времени основой для измерения времени служили астрономические наблюдения за движением Солнца и звезд. Суточное движение Солнца и звезд происходит из-за вращения Земли вокруг своей оси.

Сутки делятся на 24 часа, 1 час - на 60 минут, 1 минута - на 60 секунд; поэтому 1 секунда равна 1/24·60·60 доле суток. Длительность суток определялась из астрономических наблюдений. Однако точные современные часы позволяют обнаружить, что из-за изменения направления ветров и океанских течений, из-за влияния приливов вращение Земли вокруг своей оси то ускоряется, то замедляется. Строго повторяющимися являются периодические процессы в мире атомов. Поэтому для точных измерений времени используются атомные часы. Секунда равна 9192631770 периодам излучения атома цезия при переходе между двумя уровнями сверхтонкой структуры основного состояния.

В Международной системе единиц (СИ) длина и время приняты за независимые от других величины. Подобные величины называются основными. Длина и время - основные величины в Международной системе единиц, они используются для определения других величин этой системы.

Система отсчета. Относительность механического движения. Чтобы описать механическое движение тела (точки), нужно знать его координаты в любой момент времени. Для определения координат материальной точки следует прежде всего выбрать тело отсчета и связать с ним систему координат. В механике часто телом отсчета служит Земля, с которой связывается прямоугольная декартова система координат (рис. 4). Для определения положения материальной точки в любой момент времени необходимо также задать начало отсчета времени.

Рис. 4

Система координат, тело отсчета, с которым она связана, и указание начала отсчета времени образуют систему отсчета, относительно которой рассматривается движение тела.

Траектория движения тела, пройденный путь и перемещение зависят от выбора системы отсчета. Другими словами, механическое движение относительно.

Скорость. Для количественной характеристики процесса движения тела вводится понятие скорости движения.

Мгновенной скоростью поступательного движения тела в момент времени называется отношение очень малого перемещения к малому промежутку времени , за который произошло это перемещение:

. (1.1)

Мгновенная скорость - векторная величина.

При последовательном уменьшении длительности промежутка времени направление вектора перемещения приближается к касательной в точке A траектории движения, через которую проходит тело в момент времени (рис. 5). Поэтому вектор скорости лежит на касательной к траектории движения тела в точке A и направлен в сторону движения тела.

Рис. 5

Формула (1.1) позволяет установить единицу скорости.

В Международной системе (СИ) единицей расстояния является метр, единицей времени - секунда; поэтому скорость выражается в метрах в секунду:

.

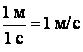Метр в секунду равен скорости прямолинейно и равномерно движущейся точки, при которой точка за время 1 с перемещается на расстояние 1 м.

Равномерное прямолинейное движение. Движение с постоянной по модулю и направлению скоростью называется равномерным прямолинейным движением. При равномерном прямолинейном движении тело движется по прямой и за любые равные промежутки времени проходит одинаковые пути.

Классический закон сложения скоростей. Выясним, как связаны между собой скорости движения тела в различных системах отсчета. Рассмотрим такой пример. Вагон движется по прямолинейному участку железнодорожного пути равномерно со скоростью относительно Земли. Пассажир движется относительно вагона со скоростью , векторы скоростей и имеют одинаковое направление. Найдем скорость пассажира относительно Земли. Перемещение пассажира относительно Земли за малый промежуток времени равно сумме перемещений за этот промежуток времени вагона относительно Земли и пассажира относительно вагона (рис. 6):

или .

Рис. 6

Отсюда скорость пассажира относительно Земли равна

(1.2)

Мы получили, что скорость пассажира в системе отсчета, связанной с Землей, равна сумме скоростей пассажира в системе отсчета, связанной с вагоном, и вагона относительно Земли.

Этот вывод справедлив для любых направлений векторов скорости и скорости . Закон, выражаемый формулой (1.2), называется классическим законом сложения скоростей.

2. Скорость

Для характеристики движения материальной точки вводят векторную физическую величину - скорость, определяющую как быстроту движения, так и направление движения в данный момент времени.

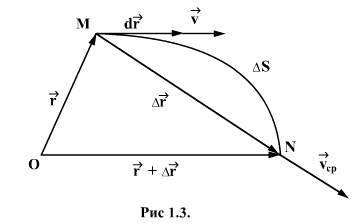
Пусть материальная точка движется по криволинейной траектории МN так, что в момент времени t она находится в т.М, а в момент времени в т. N. Радиус-векторы точек М и N соответственно равны , а длина дуги МN равна (рис. 1.3).

Вектором средней скорости точки в интервале времени от t до t+Δt называют отношение приращения радиуса-вектора точки за этот промежуток времени к его величине :

(1.5)

Вектор средней скорости направлен также, как вектор перемещения т.е. вдоль хорды МN.

Мгновенная скорость или скорость в данный момент времени. Если в выражении (1.5) перейти к пределу, устремляя к нулю, то мы получим выражение для вектора скорости м.т. в момент времени t прохождения ее через т.М траектории.

(1.6)

В процессе уменьшения величины точка N приближается к т.М, и хорда МN, поворачиваясь вокруг т.М, в пределе совпадает по направлению с касательной к траектории в точке М. Поэтому вектор и скорость v движущейся точки направлены по касательной траектории в сторону движения. Вектор скорости v материальной точки можоразложить на три составляющие, направленные вдоль осей прямоугольной декартовой системы координат.

(1.7)

где - проекции вектора скорости на оси координат х, у, z.

Подставляя в (1.6) значения для радиус-вектора материальной точки (1.1) и выполнив почленное дифференцирование, получим:

(1.8)

Из сопоставления выражений (1.7) и (1.8) следует, что проекции скорости материальной точки на оси прямоугольной декартовой системы координат равны первым производным по времени от соответствующих координат точки:

(1.9)

Поэтому численное значение скорости:

(1.10)

Движение, при котором направление скорости материальной точки не изменяется, называется прямолинейным. Если численное значение мгновенной скорости точки остается во время движения неизменным, то такое движение называется равномерным.

Если же за произвольные равные промежутки времени точка проходит пути разной длины, то численное значение ее мгновенной скорости с течением времени изменяется. Такое движение называют неравномерным.

В этом случае часто пользуются скалярной величиной , называемой средней путевой скоростью неравномерного движения на данном участке траектории. Она равна численному значению скорости такого равномерного движения, при котором на прохождение пути затрачивается то же время , что и при заданном неравномерном движении:

(1.11)

Т.к. только в случае прямолинейного движения с неизменной по направлению скоростью, то в общем случае:

.

Закон сложения скоростей. Если материальная точка одновременно участвует в нескольких движениях, то результирующее перемещения в соответствии с законом независимости движения, равно векторной (геометрической) сумме элементарных перемещений, обусловленных каждым из этих движений в отдельности:

В соответствии с определением (1.6):

(1.12)

Таким образом, скорость результирующего движения равна геометрической сумме скоростей всех движений, в которых участвует материальная точка, (это положение носит название закона сложения скоростей).