F1.Матрица. Действие над матрицей.

Ма́трица — математический объект, записываемый в виде прямоугольной таблицы чисел и допускающий алгебраические операции (сложение, вычитание, умножение) между ним и другими подобными объектами. Обычно матрицы представляются двумерными (прямоугольными) таблицами. Иногда рассматривают многомерные матрицы или матрицы непрямоугольной формы. Правила выполнения операций над матрицами сделаны такими, чтобы было удобно записывать системы линейных уравнений. У каждого элемента матрицы есть 2 нижних индекса (a_ij) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размерности », подразумевая, что в матрице m строк и n столбцов. В одной матрице всегда , Действие над матрицами. Пусть a_ij — элементы матрицы A, а b_ij — элементы матрицы B. Линейные операции: Умножение матрицы A на число λ заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен b_ij = λa_ij. Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен c_ij = a_ij + b_ij. Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой c_ij = a_ij - b_ij Сложение и вычитание допускается только для матриц одинакового размера. Произведение матрицы А на матрицу В определяется в предположении, что число столбцов матрицы А равно числу строк матрицы В. Произведением двух матриц А = (a_{i j}) и B = (b_{j k}), где i = , j= , k= , заданных в определенном порядке АВ, называется матрица С = (c _{i k}), элементы которой определяются по следующему правилу: c _{i k} = a_{i 1} b_{1 k} + a_{i 2} b_{2 k} +... + a_{i m} b_{m k} = a_{i s} b_{s k}.      Иначе говоря, элементы матрицы-произведения определяются следующим образом: элемент i-й строки и k-го столбца матрицы С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы.

Элементарными преобразованиями строк матрицы называются следующие преобразования: 1. Умножение строки на число отличное от нуля. 2. Прибавление одной строки, умноженной на число, к другой строке. 3. Перестановка местами двух строк. Элементарные преобразование столбцов матрицы определяются аналогично. Транспонирование матрицы (обозначение: A^T) — операция, при которой матрица отражается относительно главной диагонали, то есть Если A — матрица размера , то A^T — матрица размера

2. Свойство операций над матрицами.

Свойства умножения матриц: Умножение матриц не коммутативно, т.е. АВ ≠ ВА даже если определены оба произведения. Однако, если для каких - либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными. Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера. Перестановочными могут быть только квадратные матрицы одного и того же порядка. А × Е = Е × А = А

Операция умножения матриц обладает следующими свойствами: 1) (AB)C=A(BC); (Свойство ассоциативности) 2) α(АВ)=(αА)В, для любого действительного числа 3) A(B+C)=AB+AC, (A+B)C=AC+BC (Свойство дистрибутивности), для любых матриц A, B, C, для которых левые части равенств имеют смысл. Справедливость свойств 2) и 3) доказываются непосредственно. В качестве иллюстрации приведём доказательство первого равенства свойства 3). Пусть , , . Матрицы A(B+C) и AB+AC имеют одинаковый размер - . Пусть - элемент матрицы A(B+C) в позиции (i,j), - элемент матрицы AB+AC в позиции (i,j), тогда

Из равенств (1) и (2) следует, что , что доказывает первое равенство свойства 3). Заметим, что для любой матрицы и единичных матрицы и справедливо:

Операция транспонирования матриц обладает следующими свойствами:

1) ; 2) , для любого действительного числа ; 3) ; 4) , для любых матриц A и B, для которых имеют смысл левые части равенств. Свойства сложения матриц и умножения матрицы на число: Операции сложения матриц и умножения матрицы на число обладают следующими свойствами: 1. А + В = В + А; 2. А + (В + С) = (А + В) + С; 3. А + 0 = А; 4. А - А = 0; 5. 1 × А = А; 6. α × (А + В) = αА + αВ; 7. (α + β) × А = αА + βА; 8. α × (βА) = (αβ) × А; где А, В и С - матрицы, α и β - числа.

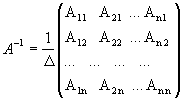
3. Обратная матрица.

Матрица A^-1 называется обратной матрицей А, если выполняется условие AA^-1=A^-1A=E. Где Е – единичная матрица того же порядка, что и матрица А. Матрица А имеет те же размеры что и матрица A^{-1 .} Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если  = 0.Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.Теорема. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Матрица, обратная матрице А, обозначается через А^1, так что В = А^1. Обратная матрица вычисляется по формуле где А _{i j} - алгебраические дополнения элементов a _{i j}.

4. Элементарные матрицы. Элементарными преобразованиями матрицы назовем следующие преобразования:             1) умножение строки на число, отличное от нуля; 2) прибавление к элементам одной строки элементов другой строки; 3) перестановка строк; 4) вычеркивание (удаление) одной из одинаковых строк (столбцов); 5) транспонирование; Те же операции, применяемые для столбцов, также называются элементарными преобразованиями. С помощью элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк (столбцов). Элементарными преобразованиями строк называют: 1) перестановка местами любых двух строк матрицы; 2) умножение любой строки матрицы на константу , к≠0 прибавление к любой строке матрицы другой строки, умноженной на константу ,. к≠0 В некоторых курсах линейной алгебры перестановка местами двух строк матрицы не вносятся в определение элементарных преобразований так как перестановку местами любых двух строк матрицы можно получить используя умножение любой строки матрицы на константу , к≠0 и прибавление к любой строке матрицы другой строки, умноженной на константу ,. к≠0 Аналогично определяются элементарные преобразования столбцов. Элементарные преобразования обратимы. Обозначение указывает на то, что матрица А может быть получена из В путём элементарных преобразований (или наоборот).

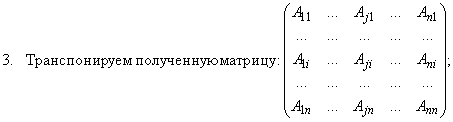
5. Вычисление обратной матрицы.  Свойства обратной матрицы (справедливы для любых невырожденных матриц): 1) (A·B)⁻¹ = B⁻¹·A⁻¹; 2) (A⁻¹)⁻¹= A; 3) I ⁻¹= I; 4) det (A⁻¹) = (det A)⁻¹; 5) A·A⁻¹·A = A; матрица, обратная к диагональной матрице — диагональная матрица; матрица, обратная к треугольной матрице — треугольная матрица; матрица, обратная к симметричной матрице — симметричная матрица.    Порядок операций при вычислении обратной матрицы:  

      

   

   

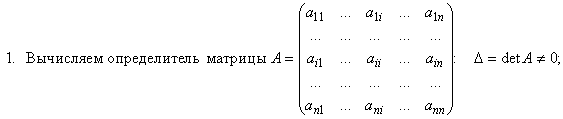
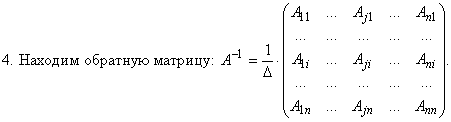
6. Линейная зависимость и независимость системы векторов. Линейной комбинацией векторов e₁,e₂, ..., e_k линейного пространства L называется выражение С₁·e₁+С₂·e₂+ ...+С_k· e_k . Числа С₁, С₂, ..., С_k — коэффициенты линейной комбинации. Если все коэффициенты линейной комбинации С₁·e₁+С₂·e₂+ ...+С_k· e_k равны нулю, то она называется тривиальной линейной комбинацией. Система e₁,e₂, ..., e_k линейно независима, если равенство С₁·e₁+С₂·e₂+ ...+С_k· e_k = 0 возможно только для тривиальной линейной комбинации. Система e₁,e₂, ..., e_k линейно зависима, если существует нетривиальная линейная комбинация, для которой справедливо равенство С₁·e₁+С₂·e₂+ ...+С_k· e_k = 0. Свойства: 1) линейно зависимо; 2) M линейно независимо M' линейно независимо для всех 3) M линейно зависимо M' линейно зависимо для всех .

7. Эквивалентные системы векторов.

8. Понятие базиса системы векторов. Ба́зис — множество векторов в векторном пространстве, таких, что любой вектор пространства может быть единственным образом представлен в виде их линейной комбинации. Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов. Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов. Базис в пространстве позволяет однозначно сопоставить каждому вектору упорядоченную тройку чисел – коэффициенты представления этого вектора в виде линейной комбинации векторов базиса. Наоборот, каждой упорядоченной тройке чисел при помощи базиса мы сопоставим вектор , если составим линейную комбинацию . Числа – называются компонентами (или координатами) вектора в данном базисе (записывается

9. Ранг конечной системы векторов. Рассмотрим систему векторов, где . Максимальной линейно независимой подсистемой системы векторов называется любой набор векторов последней, удовлетворяющий следующим условиям: векторы этого набора линейно независимы; всякий вектор из системы линейно выражается через векторы этого набора. В общем, система векторов может иметь несколько разных максимальных линейно независимых подсистем. Теорема Все максимальные линейно независимые подсистемы данной системы векторов содержат одно и то же число векторов. Число векторов в максимальной линейно независимой подсистеме системы векторов называется рангом последней. Системы векторов и называются эквивалентными, если векторы системы линейно выражаются через систему векторов и наоборот. Теорема Ранги эквивалентных систем векторов равны. Операции, переводящие систему векторов (1.1) в систему, ей эквивалентную, следующие:1)изменение нумерации векторов в системе;2)удаление нулевого вектора;3)удаление вектора, являющегося линейной комбинацией остальных векторов системы;4)умножение произвольного вектора системы на любое, не равное нулю число;5)прибавление к одному из векторов системы линейной комбинации остальных векторов системы.

10. Метод Гаусса. Метод Гаусса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Состоит в постепенном понижении порядка системы и исключении неизвестных Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Решить систему уравнений методом Гаусса: x +  y - 3z = 2; 3x - 2y +  z = - 1; 2x +  y - 2z = 0.

11. Векторное пространство. Векторное пространство, математическое понятие, обобщающее понятие совокупности всех (свободных) векторов обычного трёхмерного пространства. Определение В. п. Для векторов трёхмерного пространства указаны правила сложения векторов и умножения их на действительные числа. В применении к любым векторам х, у, z и любым числам a, b эти правила удовлетворяют следующим условиям (условия А):  1) х + у = у + х (перестановочность сложения);  2) (х + у) + z = x + (y + z) (ассоциативность сложения);  3) имеется нулевой вектор 0 (или нуль-вектор), удовлетворяющий условию x + 0 = x: для любого вектора x; 4) для любого вектора х существует противоположный ему вектор у такой, что х + у = 0,  5) 1 · х = х,  6) a(bx) = (ab) х (ассоциативность умножения); 7) (a + b) х = aх + bх (распределительное свойство относительно числового множителя);   8) a(х + у) = aх + aу (распределительное свойство относительно векторного множителя). Векторным пространством называется множество R, состоящее из элементов любой природы (называемых векторами), в котором определены операции сложения элементов и умножения элементов на действительные числа, удовлетворяющие условиям А. Выражение  a₁e₁ + a₂e₂ + … + a_ne_n (1) называется линейной комбинацией векторов e₁, e₂,..., e_n с коэффициентами a₁, a₂,..., a_n. Линейная комбинация (1) называется нетривиальной, если хотя бы один из коэффициентов a₁, a₂,..., a_n отличен от нуля. Векторы e₁, e₂,..., e_n называются линейно зависимыми, если существует нетривиальная комбинация (1), представляющая собой нулевой вектор. В противном случае (то есть если только тривиальная комбинация векторов e₁, e₂,..., e_n равна нулевому вектору) векторы e₁, e₂,..., e_n называется линейно независимыми.  БАЗИС ВЕКТОРНОГО ПРОСТРАНСТВА — набор из максимального числа линейно независимых векторов. Следовательно, все остальные векторы пространства оказываются линейными комбинациями базисных. Если все базисные векторы взаимно ортогональны, а длина каждого из них равна единице, то базис называется ортонормированным. Единичный базисный вектор называют ортом (обозначается e_i, где i — номер координаты).Каждый вектор пространства может быть представлен в виде линейной комбинации базисных векторов: a = ∑a_ie_i. Коэффициенты разложения ai однозначно определяют вектор a. Поэтому часто говорят, что n-мерный вектор — это упорядоченная совокупность n чисел {a_i}. Размерность векторного пространства равна количеству векторов, составляющих его базис.

12. Координаты вектора относительного базиса.

13. Геометрический вектор. 1) Геометрический вектор - это направленный отрезок прямой. В математике рассматриваются только свободные векторы, т.е. векторы, начало которых выбирают произвольно. Обозначается вектор: a, , , . Вектор (рис.13) характеризуется модулем (длиной), который равен длине отрезка АВ и обозначается или , и направлением: от А к В. 2) Вектор, начало и конец которого совпадают, называется нулевым вектором, обозначается или 0, направление этого вектора не определяется. Вектор называется противоположным вектору , для вектора противоположный обозначается - .Вектор единичной длины называется единичным вектором или ортом. Два вектора называются равными, если они имеют равные модули и одинаково направлены, записывают: .Ненулевые векторы называют коллинеарными, если они лежат на одной или на параллельных прямых, обозначают . Коллинеарные векторы называют сонаправленными, если их направления совпадают, обозначают . Ненулевые векторы называются компланарными, если они лежат в одной или в параллельных плоскостях. 3) Линейными операциями над векторами называют сложение векторов и умножение вектора на число. 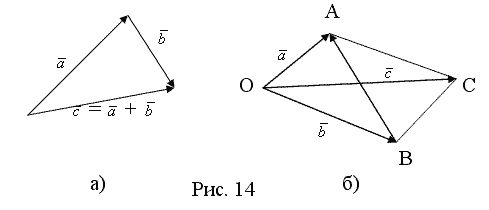Суммой векторов и называется вектор , который можно найти:а) по правилу треугольника (рис. 14а); б) по правилу параллелограмма (рис. 14б). Напомним, что в параллелограмме ОАСВ (рис. 14) сумма есть вектор-диагональ , исходящая из общего начала О векторов и , а разность этих векторов есть другая вектор-диагональ - вектор, направленный из конца вычитаемого вектора к концу уменьшаемого.

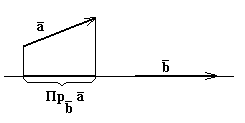
14.Вычитание, умножение векторов на скаляр. Вычитание векторов. Чтобы из вектора а вычесть вектор b надо к вектору а прибавить вектор, противоположный вектору b. Полученный в результате этой операции вектор с и будет являться разностью векторов а и b. Таким образом,с = а − b = а + (− b).Рисунок иллюстрирует операцию вычитания векторов.

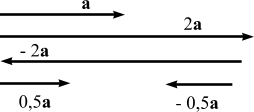
Умножение вектора на скаляр. Умножение вектора а на скаляр m даёт вектор, модуль которого в m раз отличается от модуля вектора а, и направленный в сторону а, если m > 0 и в противоположную, если m < 0. Символически эта операция записывается в виде равенства, например, с = ma. Рисунок иллюстрирует эту операцию. Рассматриваемая операция удовлетворяет соотношению m (a + b) = ma + mb. В этом случае говорят, что умножение вектора на скаляр дистрибутивно, то есть для него выполняется распределительный закон. В векторной алгебре рассматривается не только умножение вектора на скаляр, но и умножение векторов. Следует иметь в виду, что возможны различные способы умножения векторов. Из всего многообразия этих способов мы рассмотрим только два, поскольку они чаще других применяются при изучении физических явлений. В следующих пунктах бокового меню будут рассмотрены скалярное и векторное произведения двух векторов.

15. Скалярное произведение векторов.

Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю. Обычно используется одно из следующих обозначений: , , , Скалярным произведением в линейном пространстве называется функция , принимающая числовые значения, определенная для каждой пары элементов и удовлетворяющая следующим условиям: 1. для любых трех элементов и пространства и любых чисел справедливо равенство [линейность скалярного произведения по первому аргументу];2. для любых и справедливо равенство ,где черта означает комплексное сопряжение [эрмитова симметричность];

3. для любого имеем ,причем только при [положительная определенность скалярного произведения].Действительное линейное пространство со скалярным произведением называется евклидовым, комплексное — унитарным.скалярное произведение обозначается , или , или . Скалярное произведение вектора на себя, a*a, обозначается . Скалярное произведение обладает следующими свойствами, которые мы сформулируем в виде теоремы. Для любых векторов a и b выполнены следующие соотношения: 1) , свойство коммутативности; 2)а(b+c)=ab+ac, свойство дистрибутивности; 3) ; 4) при ; 5) ; 6) Если  -- угол между векторами a и b, то ; 7) , если ; 8) тогда и только тогда, когда векторы a и b ортогональны.

16. Метод координат на плоскости. Метод координат заключается в установлении соответствия между точками прямой (плоскости, пространства) и их координатами — действительными числами при помощи системы координат.координаты, точки плоскости получают, выбирая точку 0 (начало координат) и два нележащих на одной прямой вектора  и  (базисных вектора), исходящих из точки . Положение точки М определяется (в выбранной системе координат) двумя координатами: абсциссой и ординатой где ХМ параллельно ОВ и УМ параллельно ОА (рис. 1, где х=2, у=-1).В частном случае, когда векторы  и  перпендикулярны и имеют одну и ту же длину, получают наиболее употребительные прямоугольные координаты. Если угол между  и  произволен, но длины этих векторов одинаковы, то получают те косоугольные координаты, рассмотрением которых ограничивался сам Определение. Пусть L – произвольная прямая,  – её произвольные точки, причем . Говорят, что точка С делит отрезок АВ, считая от точки А, в отношении , если .Замечание. Из определения следует, что точки С и В не могут совпадать, ибо в противном случае, т.е. если , то , откуда следует, что , что противоречит предположению .   Далее, число , если , то , откуда следует, что .

17. Геометрическое истолкование уравнений.

18. Параметрические уравнения прямой. Так как этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой. Это векторное уравнение может быть представлено в координатной форме: Преобразовав эту систему и приравняв значения параметра t, получаем канонические уравнения прямой в пространстве:

 19. Общее уравнение прямой на плоскости. Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А² + В² ¹ 0. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи: 1) C = 0, А ¹ 0, В ¹ 0 – прямая проходит через начало координат; 2) А = 0, В ¹ 0, С ¹ 0 { By + C = 0}- прямая параллельна оси Ох; 3)В = 0, А ¹ 0, С ¹ 0 { Ax + C = 0} – прямая параллельна оси Оу; 4) В = С = 0, А ¹ 0 – прямая совпадает с осью Оу; 5) А = С = 0, В ¹ 0 – прямая совпадает с осью Ох. Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.

20. Уравнение прямой на плоскости через 2 точки.          Пусть в пространстве заданы две точки M₁(x₁, y₁, z₁) и M₂(x_2, y₂, z₂), тогда уравнение прямой, проходящей через эти точки: Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.            На плоскости записанное выше уравнение прямой упрощается: если х₁ ¹ х₂  и х = х₁, еслих₁ = х₂. Дробь = k называется угловым коэффициентом прямой.

Уравнение прямой в отрезках. Если в общем уравнении прямой Ах + Ву + С = 0 С≠ 0, то, разделив на –С, получим:  или , где Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.

21. Уравнение прямой с угловым коэффициентом. Уравнение y  =  kx  +  b называется уравнением прямой с угловым коэффициентом k . Любая прямая, не перпендикулярная оси OX , может быть определена этим уравнением. Прямая же, перпендикулярная оси абсцисс, задается уравнением x  =  x ₀. Отметим, что вертикальная прямая не является графиком функции. Итак, уравнением y  =  kx  +  b можно описать не любую прямую. Этого недостатка нет у так называемого общего уравнения прямой a   x  +  b   y  =  c       ( a ²  +  b ²  ≠ 0). Если b  = 0, то – получаем уравнение вертикальной прямой. Если же b  ≠ 0, то Таким образом, угловой коэффициент прямой в этой системе обозначений задается как

Определение. Если заданы две прямые y = k₁x + b₁,  y = k₂x + b₂, то острый угол между этими прямыми будет определяться как .Две прямые параллельны, если k₁ = k₂.

Две прямые перпендикулярны, если k₁ = -1/k₂. Теорема. Прямые Ах + Ву + С = 0 и А₁х + В₁у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = lА,  В₁ = lВ. Если еще и С₁ = lС, то прямые совпадают. Координаты точки пересечения двух прямых находятся как решение системы  уравнений этих прямых.

22. Нормальное уравнение прямой. Если обе части уравнения Ах + Ву + С = 0 разделить на число , которое называется нормирующем множителем, то получим xcosj + ysinj - p = 0 – нормальное уравнение прямой.Знак ± нормирующего множителя надо выбирать так, чтобы m×С < 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а j - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

Расстояние от точки до прямой: Теорема. Если задана точка М(х₀, у₀), то расстояние до прямой Ах + Ву + С =0 определяется как Доказательство. Пусть точка М₁(х₁, у₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁:    Координаты x₁ и у₁ могут быть найдены как решение системы уравнений: Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М₀ перпендикулярно заданной прямой. Если преобразовать первое уравнение системы к виду: A(x – x₀) + B(y – y₀) + Ax₀ + By₀ + C = 0, то, решая, получим: 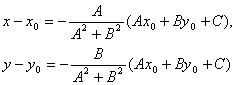Подставляя эти выражения в уравнение (1), находим: .

23. Определители.

 Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Определитель матрицы является многочленом от элементов квадратной матрицы (т.е. такой, у которой количество строк и столбцов равны). В общем случае матрица может быть определена над любым коммутативным кольцом, в этом случае определитель будет элементом того же кольца.Определитель матрицы А обозначается как: det(A), |А| или Δ(A).

Свойства: 1) Детерминант — кососимметричная полилинейная функция строк (столбцов) матрицы. Полилинейность означает, что определитель линеен по всем строкам (столбцам): , где и т. д. — строчки матрицы, — определитель такой матрицы.

2) При добавлении к любой строке (столбцу) линейной комбинации других строк (столбцов) определитель не изменится. 3) Если две строки (столбца) матрицы совпадают, то её определитель равен нулю. 4) Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя. 5) Если хотя бы одна строка (столбец) определителя нулевая, то определитель равен нулю. 6) Сумма произведений всех элементов любой строки на их алгебраические дополнения равна определителю. 7) Сумма произведений всех элементов любого ряда на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю. 8) Определитель произведения матриц равен произведению их определителей. 9) С использованием индексной нотации определитель матрицы может быть определён с помощью символа Леви-Чивита из соотношения:

24. Прямоугольная система координат в пространстве.

Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей(что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат. Положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Такая система координат называется правой. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси. Расстояние d между двумя точками ( , , ) и ( , , ) в пространстве определяется формулой .Координаты x, y, z точки М, которая делит отрезок , ограниченный точками ( , , ) и ( , , ), в отношении , определяется по формулам , , .В частности, при имеет координаты середины данного отрезка: , , .

25. Векторное произведение векторов.

Векторным произведением векторов и  называется вектор , удовлетворяющий следующим условиям:1) , где j - угол между векторами и , ; 2) вектор ортогонален векторам и ; 3) , и  образуют правую тройку векторов.Обозначается:  или .  Свойства векторного произведения векторов:1) ;2) , если ïï  или = 0 или = 0;3) (m )´ = ´(m ) = m( ´ );4) ´( + ) = ´ + ´ ; 5) Если заданы векторы (x_a, y_a, z_a) и (x_b, y_b, z_b) в декартовой прямоугольной системе координат с единичными векторами , то ´ =  

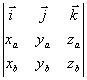
6) Геометрическим смыслом векторного произведения векторов является площадь параллелограмма, построенного на векторах и .

26. Смешанное произведение векторов. Сме́шанное произведе́ние векторов  — скалярное произведение вектора на векторное произведение векторов и : . Иногда его называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр). Геометрический смысл: Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами . Свойства: 1) Смешанное произведение кососимметрично по отношению ко всем своим аргументам: т. е. перестановка любых двух сомножителей меняет знак произведения. Отсюда следует, что ; 2) Смешанное произведение в правой декартовой системе координат (в ортонормированном базисе) равно определителю матрицы, составленной из векторов и : В частности; 3)Если три вектора линейно зависимы (т. е. компланарны, лежат в одной плоскости), то их смешанное произведение равно нулю. 4) Геометрический смысл — Смешанное произведение по абсолютному значению равно объёму параллелепипеда (см. рисунок), образованного векторами и ; знак зависит от того, является ли эта тройка векторов правой или левой. Три вектора, определяющие параллелепипед. Смешанное произведение удобно записывается с помощью символа (тензора) Леви-Чивиты: (в последней формуле в ортонормированном базисе все индексы можно писать нижними; в этом случае эта формула совершенно прямо повторяет формулу с определителем, правда, при этом автоматически получается множитель (-1) для левых базисов).

27. Параметрические уравнения плоскости в пространстве.

28. Общее уравнение прямой. Общим уравнение плоскости в пространстве называется равнение виды Ах+Ву+Сz+D=0 где A² + B² + C² ≠ 0 . В трехмерном пространстве в декартовой системе координат любая плоскость описывается линейным уравнением. В трехмерном пространстве в декартовой системе координат любое линейное уравнение определяет плоскость. Возможны следующие частные случаи: 1) А = 0 – плоскость параллельна оси Ох; 2) В = 0 – плоскость параллельна оси Оу; 3) С = 0 – плоскость параллельна оси Оz; 4) D = 0 – плоскость проходит через начало координат; 5) А = В = 0 – плоскость параллельна плоскости хОу; 6)А = С = 0 – плоскость параллельна плоскости хОz; 7) В = С = 0 – плоскость параллельна плоскости yOz; 8) А = D = 0 – плоскость проходит через ось Ох; 9)В = D = 0 – плоскость проходит через ось Оу; 10) С = D = 0 – плоскость проходит через ось Oz; 11) А = В = D = 0 – плоскость совпадает с плоскостью хОу; 12) А = С = D = 0 – плоскость совпадает с плоскостью xOz; 13) В = С = D = 0 – плоскость совпадает с плоскостью yOz;

29. Уравнение плоскости, проходящей через 3точки.             Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.           Рассмотрим точки М₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃) в общей декартовой системе координат.Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М₁, М₂, М₃ необходимо, чтобы векторы  были компланарны.

( ) = 0 Таким образом, 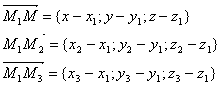   Уравнение плоскости, проходящей через три точки: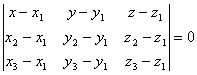

30. Угол между двумя плоскостями.     Угол между двумя плоскостями в пространстве j связан с углом между нормалями к этим плоскостям j₁ соотношением: j = j₁ или j = 180⁰ - j₁, т.е. cosj = ±cosj₁. Определим угол j₁. Известно, что плоскости могут быть заданы соотношениями: , где

(A₁, B₁, C₁), (A₂, B₂, C₂). Угол между векторами нормали найдем из их скалярного произведения: . Таким образом, угол между плоскостями находится по формуле:    Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.

31. Параметрические уравнения прямой в пространстве.

32. Прямая как линия пересечения двух плоскостей. Угол между прямыми в пространстве: Пусть в пространстве заданы две прямые. Их параметрические уравнения: l₁:   ; l₂:   Угол между прямыми j и угол между направляющими векторами j этих прямых связаны соотношением: j = j₁ или j = 180⁰ - j₁. Угол между направляющими векторами находится из скалярного произведения. Таким образом:

33. Эллипс. Э́ллипс — геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек F₁ и F₂ (называемых фокусами) постоянна, то есть | F₁M | + | F₂M | = 2a.Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой. Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость. Свойства: 1) Оптическое свойство. Если F₁ и F₂ — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой (F₁X) равен углу между этой касательной и прямой (F₂X). 2) Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы. 3)Эволютой эллипса является астроида. Эллипс также можно описать как: а) фигуру, которую можно получить из окружности, применяя аффинное преобразование; б) ортогональную проекцию окружности на плоскость. в) Пересечение плоскости и кругового цилиндра

34. Гипербола. Гипе́рбола   — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F₁ и F₂ (называемых фокусами) постоянно, то есть | | F₁M | − | F₂M | | = C. Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы. Термин «гипербола» (греч.— избыток) был введён Аполлонием Пергским, поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком. Обратной пропорциональностью называют функцию, заданную формулой y = k/x где k неравно 0. Число k называется коэффициентом обратной пропорциональности. Если считать х независимой переменной, а у — зависимой, то формула y = k/x определяет у как функцию от х. График функции y = k/x называют гиперболой. Гипербола имеет две ветви, которые расположены в первом и третьем квадратах, если k > 0, и во втором и четвертом квадрантах, если k > 0. Функция y = k/x , где k > 0 обладает следующими свойствами: 1) область определения функции — множество всех действительных чисел, за исключением числа; 2) множество значений функции, все числа кроме числа 0; 3)y = k/x — нечетная; 4) принимает положительные значения при х > 0 и отрицательные — при x < 0; 5) убывает на промежутках х < 0 и х > 0. Если k < 0, то функция y = k/x обладает свойствами 1—3, а свойства 4—5 формулируются так: принимает положительные значения при х < 0 и отрицательные при х > 0; 6) возрастает на промежутках х < 0 и х > 0.;

35. Парабола. Пара́бола (греч. — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом. Свойства: 1) Парабола — кривая второго порядка; 2) Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и перпендикулярна директрисе; 3) Пучок лучей параллельных оси, отражаясь в параболе собирается в её фокусе. Для параболы y² = x фокус находится в точке (0,25; 0); 4) Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе; 5) Парабола является антиподерой прямой; 6) Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб; 7) При вращении параболы вокруг оси симметрии получается эллиптический параболоид. Антиподера — кривая, для которой данная кривая является подерой. Для параметрически заданной плоской кривой антиподера относительно начала координат определяется следующими уравнениями: ,

36. Функция. В математике числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множества действительных чисел или множества комплексных чисел . Пусть дано отображение . Тогда его гра́фиком Γ называется множество , где обозначает декартово произведение множеств X и Y. 1) Графиком непрерывной функции является кривая на двумерной плоскости; 2) Графиком непрерывной функции является поверхность в трёхмерном пространстве. Арифметическая функция — функция, определенная на множестве натуральных чисел , и принимающая значения во множестве комплексных чисел . Как следует из определения, арифметической функцией называется любая функция . Название арифметическая функция связано с тем, что в теории чисел известно много функций натурального аргумента , которые выражают те или иные арифметические свойства . Поэтому, неформально говоря, под арифметической функцией понимают функцию , которая «выражает некоторое арифметическое свойство» натурального числа . Многие арифметические функции, рассматриваемые в теории чисел, в действительности являются целозначными. Операции: Суммой арифметической функции f называют функцию , определённую как . Эта операция является «дискретным аналогом» неопределённого интеграла; при этом, хотя исходная функция и была определена только на , её сумму оказывается удобным считать определённой на всей положительной полуоси (при этом она, естественно, кусочно-постоянна). Свёрткой Дирихле (англ.) двух арифметических функций f и g называется арифметическая функция h, определённая по правилу h(n)= ∑ f(d)g(n/d), d/n;

• Арифметической функции f можно сопоставить её «производящую функцию» — ряд Дирихле

Φf(s) =	∑	f(n)n − s.
	n

При этом свёртке Дирихле двух арифметических функций соответствует произведние их производящих функций.

• Поточечное умножение на логарифм,

является дифференцированием алгебры арифметических функций: относительно свёртки оно удовлетворяет правилу Лейбница,

(f * g)' = f' * g + f * g'.

Переход к производящей функции превращает эту операцию в обычное дифференцирование.

36. Функция. В математике числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множества действительных чисел или множества комплексных чисел . Пусть дано отображение . Тогда его гра́фиком Γ называется множество , где обозначает декартово произведение множеств X и Y. 1) Графиком непрерывной функции является кривая на двумерной плоскости; 2) Графиком непрерывной функции является поверхность в трёхмерном пространстве. Арифметическая функция — функция, определенная на множестве натуральных чисел , и принимающая значения во множестве комплексных чисел . Как следует из определения, арифметической функцией называется любая функция . Название арифметическая функция связано с тем, что в теории чисел известно много функций натурального аргумента , которые выражают те или иные арифметические свойства . Поэтому, неформально говоря, под арифметической функцией понимают функцию , которая «выражает некоторое арифметическое свойство» натурального числа . Многие арифметические функции, рассматриваемые в теории чисел, в действительности являются целозначными. Операции: Суммой арифметической функции f называют функцию , определённую как . Эта операция является «дискретным аналогом» неопределённого интеграла; при этом, хотя исходная функция и была определена только на , её сумму оказывается удобным считать определённой на всей положительной полуоси (при этом она, естественно, кусочно-постоянна). Свёрткой Дирихле (англ.) двух арифметических функций f и g называется арифметическая функция h, определённая по правилу h(n)= ∑ f(d)g(n/d), d/n; Арифметической функции f можно сопоставить её «производящую функцию» — ряд Дирихле Фf(s)= ∑ f(n)n^{− s} При этом свёртке Дирихле двух арифметических функций соответствует произведние их производящих функций. Поточечное умножение на логарифм, является дифференцированием алгебры арифметических функций: относительно свёртки оно удовлетворяет правилу Лейбница, (f * g)' = f' * g + f * g'. Переход к производящей функции превращает эту операцию в обычное дифференцирование.

37. Композиция функций. Компози́ция фу́нкций — это применение одной функции к результату другой. Композиция функций F и G обычно обозначается . Термин «сложная функция» может быть применим к композиции двух функций, тем не менее он чаще употребляется в ситуации когда на вход функции нескольких переменных подаётся набор функций от одной или нескольких исходных переменных. Например функция G вида G(x,y) = F(u(x,y),v(x,y)). Свойства композиции: 1) Композиция ассоциативна: . 2) Если F = id_X — тождественное отображение на X, то есть

, то . 3) Если G = id_Y — тождественное отображение на Y, то есть , то .4) Рассмотрим пространство всех биекций множества X на себя и обозначим его . То есть если , то — биекция. Тогда композиция функций из является бинарной операцией, а — группой. id_X является нейтральным элементом этой группы. Обратным к элементу является — обратная функция. 5) Группа , вообще говоря, не коммутативна, то есть . Способы задания функций: Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами. Табличный способ. заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством. Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью. Если зависимость имеет вид y = f(x), то функция от x задана в явном виде. Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.

38. Элементарные функции. Четные и нечетные. Элементарные функции — функции, которые можно получить из основных элементарных функций: многочлен, рациональная, степенная, показательная и логарифмическая, тригонометрические и обратные тригонометрические, Гиперболические функции. с помощью конечного числа арифметических действий и композиций. Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, отвечающих перечисленным операциям. В математике, нечётные и чётные функции это функции, графики которых обладают симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Такое название возникло как обобщение чётности степенных функций: функция f(x) = xⁿ чётна тогда и только тогда, когда n чётно, и нечётна тогда и только тогда, когда n нечётно. Нечётная фу́нкция — функция, меняющая знак при изменении знака независимого переменного. Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного. Нечётная фу́нкция — функция, симметричная относительно центра координат, а чётная — функция, симметричная относительно оси ординат.

39. Ограниченные и неограниченные функции. Область определения и область значений функции. В элементарной математике изучаются функции только на множестве действительных чисел R. Это значит, что аргумент функции может принимать только те действительные значения, при которых функция определена, т.e. она также принимает только действительные значения. Множество X всех допустимых действительных значений аргумента  x, при которых функция  y = f ( x ) определена, называется областью определения функции. Множество Y всех действительных значений  y, которые принимает функция, называется областью значений функции. Теперь можно дать более точное определение функции: правило (закон) соответствия между множествами  X  и Y, по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y, называется функцией.  Из этого определения следует, что функция считается заданной, если: 1)задана область определения функции X ; 2) задана область значений функции Y ; 3)известно правило соответствия, причём такое, что для каждого; 4) значения аргумента может быть найдено только одно значение функции. Монотонная функция. Если для любых двух значений аргумента  x₁  и  x₂ из условия  x₂ > x₁ следует  f ( x₂ ) > f ( x₁ ), то функция  f ( x ) называется возрастающей; если для любых  x₁  и  x₂  из условия  x₂ > x₁ следует  f ( x₂ ) < f ( x₁ ), то функция  f ( x ) называется убывающей. Функция, которая только возрастает или только убывает, называется монотонной. Ограниченная и неограниченная функции. Функция называется  ограниченной, если существует такое положительное число M, что |  f ( x ) |  M  для всех значений  x . Если такого числа не существует, то функция - неограниченная. Рис 3.-ограниченная, немонотонная. Рис. 4 – не ограниченная, монотонная.

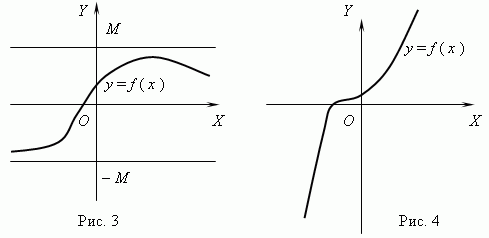
40. Обратимые функции.

Пусть задана функция y = f (x), Тогда каждому числу соответствует единственное число  Иногда приходится по значению функции y₀ находить значение аргумента x₀, то есть решать уравнение f (x) = y₀  относительно x. Это уравнение может иметь несколько или даже бесконечное количество решений (решениями являются абсциссы всех точек, в которых график y = f (x) пересекается с прямой y = y₀). Если функция f такова, что каждому значению соответствует только одно значение то эту функцию называют обратимой. Для такой функции уравнение y = f (x) можно при любом y однозначно разрешить относительно x, то есть каждому соответствует единственное значение Это соответствие определяет функцию, которую называют обратной к функции f и обозначают символом f^–1. Пусть g = f^–1. Тогда: 1)D (g) = E (f), E (g) = D (f); 2)для любого   g (f (x)) = x, 3) для любого   f (g (x)) = x; 4) графики функций y = f (x) и y = g (x) симметричны друг другу относительно прямой y = x. Функцию f , будем называть обратимой, если всяким двум различным  значениям аргумента соответствуют различные значения функции.