
- •Методические указания к курсовой работе по информатике
- •Оглавление
- •Введение
- •1. Порядок выполнения
- •2. Содержание курсовой работы
- •2.1. Постановка задачи
- •2.2. Экономико-математическая модель
- •2.3. Этапы выполнения курсовой работы
- •2.3.1.Выбор вида полинома для аппроксимации доходов и прибыли.
- •2.3.2. Вычисление параметров уравнений аппроксимации
- •2.4. Анализ результатов и выводы
- •3. Варианты заданий
- •Литература
- •Учебное пособие Методические указания к курсовой работе по информатике
- •346428. Новочеркасск, ул. Просвещения, 132.
- •346500. Шахты, пл. Ленина.
2.3.2. Вычисление параметров уравнений аппроксимации
Уравнение линейной аппроксимации имеет вид:
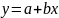 ,
,
где а – свободный член уравнения,
b – коэффициент регрессии.
Параметры a и b находятся методом наименьших квадратов (МНК).
Исходное условие МНК для прямой линии имеет вид:
 .
.
Система нормальных уравнений имеет вид:
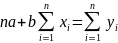
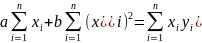
Из этой системы находим коэффициенты a и b.
Параметры уравнения можно найти методом Крамера, используя определители:
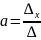 ,
,
 ,
,
где
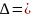
Для аппроксимации дохода используется полином 2-го порядка – парабола, которая имеет следующий вид:
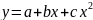 .
.
Для полинома 2-го порядка получим аналогичную систему нормальных уравнений:
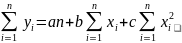
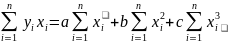
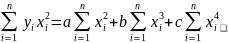
Рассмотрим решение системы уравнений методом Крамера в Excel. Расчет произведен для линейного уравнения. Аналогично поступаем для параболы.
Метод Крамера
Пусть нам требуется решить систему линейных алгебраических уравнений
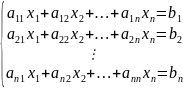
в
которой число уравнений равно числу
неизвестных переменных и определитель
основной матрицы системы отличен от
нуля, то есть, ![]() .
.
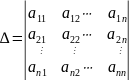 ,
, 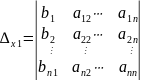 ,
,
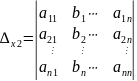 , …,
, …, 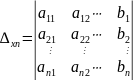
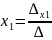 ,
, 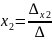 , …,
, …, 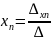
Пример решения системы линейных уравнений Система нормальных уравнений для линейной функции аппроксимации суммарных издержек |
||||||
|
|
|
|
|||
|
|
|
||||
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Δ= |
|
|
|
|
|
|
|
|
|
|
|
|
|
Δa= |
Δa=
|
|
|
|
|
|
|
|
|
|
|
|
|
Δb= |
|
|
|
|
|
|

2.4. Анализ результатов и выводы
В заключительной части пояснительной записки должны быть проанализированы полученные результаты с экономической точки зрения и сделаны выводы относительно адекватности и точности использованной математической модели и вычислительных методов. Для этого, по результатам расчетов, следует привести в аналитическом виде аппроксимирующие функции и средне –квадратичное отклонение для каждой из них, определить лучшую из функций-кандидатов для каждой из исследуемых функций, найти конкретное значение точки безубыточности.
Для оценки точности модели и вычислительных методов следует проанализировать источники возможных ошибок и погрешностей, обосновать выбор численных методов, построить график вычислительных процессов и определить точность вычислений по каждому методу и точность применяемых в программе переменных. Данную оценку следует подтвердить полученными в результате выполнения программы данными о количестве итераций, необходимых для достижения заданной точности тем или иным методов.



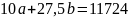


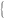

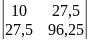 =
206,25
=
206,25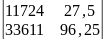 =207063,5
=207063,5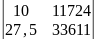 =13700
=13700