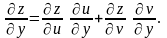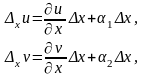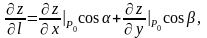- •Розділ 4 Диференціальне числення функцій кількох змінних
- •4.1. Основні поняття.
- •4.1.1. Простір Rn.
- •4.1.2. Означення функції багатьох змінних.
- •4.1.3. Графічне зображення функції двох змінних.
- •4.1.4. Знаходження області визначення функції двох змінних.
- •4.1.5. Границя функції двох змінних.
- •4.1.6. Неперервність функції двох змінних.
- •4.1.7. Неперервність складеної (складної) функції двох змінних.
- •4.1.8. Властивості неперервної функції двох змінних.
- •4.1.9. Рівномірна неперервність.
- •4.2. Диференційовність функції двох змінних.
- •4.2.1. Частинні та повні прирости функції двох змінних.
- •4.2.2. Частинні похідні двох змінних.
- •4.2.3. Повний диференціал функції двох змінних.
- •4.2.4. Частинні похідні та повний диференціал функції n-змінних.
- •Правило знаходження частинних похідних першого порядку.
- •Геометрична інтерпретація частинних похідних.
- •Властивості повного диференціала.
- •4.2.5. Достатня умова диференційованості функції двох змінних у точці.
- •4.2.6. Диференціювання складеної функції.
- •4.2.7. Похідна за напрямом. Градієнт.
- •4.2.8. Частинні похідні і повні диференціали вищих порядків.
- •4.2.9. Диференціювання неявної функції.
- •4.2.10. Формула Тейлора для функції двох змінних.
- •4.2.11. Визначник Якобі (якобіан).
- •4.3. Дослідження функцій багатьох змінних.
- •4.3.1. Поняття екстремуму функцій багатьох змінних.
- •Графічна інтерпретація.
- •4.3.2. Необхідні умови існування екстремуму.
- •В прави для самостійного розв’язування
4.2.6. Диференціювання складеної функції.
Теорема.
Нехай
на множині D
визначено складену функцію
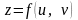 ,
де
,
де
 ,
,
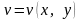 ,
і нехай функції
,
і нехай функції
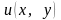 ,
,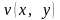 мають у деякому околі точки
мають у деякому околі точки
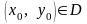 неперервні частинні
похідні, а функція
неперервні частинні
похідні, а функція
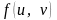 має неперервні частинні похідні в
деякому околі точки
має неперервні частинні похідні в
деякому околі точки
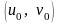 ,
де
,
де
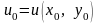 ,
, .
Тоді складена функція
.
Тоді складена функція
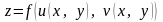 диференційовна в точці
,
причому
диференційовна в точці
,
причому
|
(4.16) |
|
(4.17) |
Доведення. За умовою теореми функції і мають неперервні частинні похідні в деякому околі точки . Тому за теоремою вони диференційовні в точці :
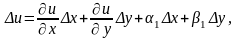

де
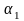 ,
,
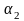 ,
,
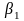 ,
,
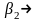 при
,
.
при
,
.
Надавши приростів лише аргументу х, дістанемо
|
(4.18) |
де
,
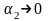 при
при
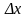 ,
,
Знайдемо приріст функції за х. За умовою теореми функція має неперервні частинні похідні в деякому околі точки , а тому вона диференційовна в цій точці:
|
(4.19) |
Підставляючи у (4.19) рівності (4.18), дістаємо:
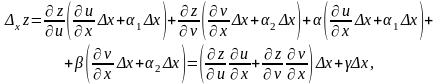
де
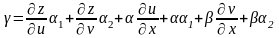 ‑
‑
нескінченно мала величина при .
Тоді
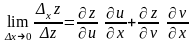 .
.
Диференційовність функції випливає з неперервності частинних похідних і .
З
найти
 і
і
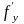 для функції
,
якщо
для функції
,
якщо
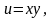

Розв’язування. За формулами (4.16) і (4.17) маємо:
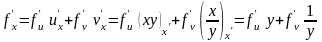 ;
;
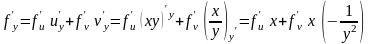 .
.
З
найти
повний диференціал функції ,
якщо
 ,
, ,
,

Розв’язування. Дістаємо:
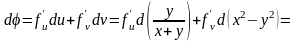
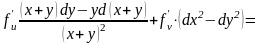
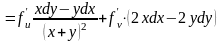 .
.
4.2.7. Похідна за напрямом. Градієнт.
Означення.
Нехай функція
визначена в деякому околі точки
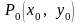 ;
l‑
деякий промінь з початком у точці
;
;
l‑
деякий промінь з початком у точці
;
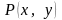 ‑
точка на цьому промені, яка належить
околу точки
(рис. 5.13);
‑
точка на цьому промені, яка належить
околу точки
(рис. 5.13);
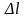 ‑
довжина відрізка
‑
довжина відрізка
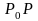 .
Якщо існує
.
Якщо існує
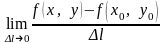 ,
то ця границя називається похідною
функції
за
напрямом l у точці
і
позначається
,
то ця границя називається похідною
функції
за
напрямом l у точці
і
позначається
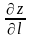 .
.
Зокрема, ‑ похідна функції за додатним напрямом осі х, а ‑ похідна функції за додатним напрямом осі у.
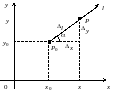
Рис. 4.13
Похідна за напрямом характеризує швидкість зміни функції у точці за напрямом l.
Теорема.
Якщо
функція
має в точці
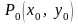 неперервні частинні похідні, то в цій
точці існує похідна
за будь-яким напрямом
неперервні частинні похідні, то в цій
точці існує похідна
за будь-яким напрямом
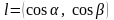 ,
причому
,
причому
|
(4.20) |
де
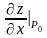 і
і
 ‑
значення частинних похідних у точці
.
‑
значення частинних похідних у точці
.
Доведення. За умовою теореми функція має в точці неперервні частинні похідні, тому вона диференційовна в цій точці:
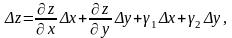
де
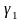 ,
,
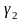 ‑
нескінченно малі величини при
Тоді
‑
нескінченно малі величини при
Тоді
 .
.
Із трикутника
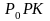 (рис.
4.13)
маємо:
(рис.
4.13)
маємо:
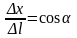 ,
,
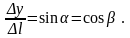
Звідси
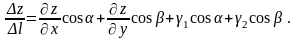
Якщо
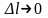 ,
то
,
,
а отже
,
то
,
,
а отже

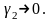 Звідси
Звідси
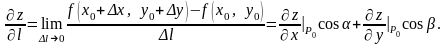
З
найти
похідну функції
 у точці
у точці
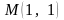 за напрямом
за напрямом
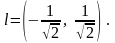
Розв’язування.
Знайдемо
та обчислимо частинні похідні в точці
 функції
функції
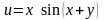 :
:

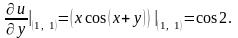
Тоді за формулою (5.2.13) маємо:
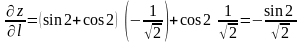 .
.
Означення.
Вектор з координатами
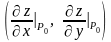 ,
який характеризує напрям максимального
зростання функції
в точці
,
називається градієнтом
функції
у
цій точці і позначається
,
який характеризує напрям максимального
зростання функції
в точці
,
називається градієнтом
функції
у
цій точці і позначається
 :
:
|
(4.21) |
де і, j‑ одиничні орти.
З
найти
градієнт функції
 у точці
у точці
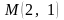 .
.
Розв’язування. Запишемо та обчислимо частинні похідні в точці :
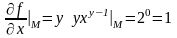 ;
;
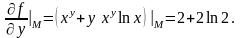
Тоді
згідно з (5.2.14)
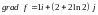 ,
або
,
або
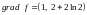 .
.
Аналогічно
для диференційовної функції
 у точці
у точці
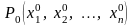 похідна
за напрямом довільного одиничного
вектора
похідна
за напрямом довільного одиничного
вектора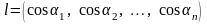 ,
,
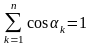 подається так:
подається так:

Означення.
Градієнтом
диференційовної функції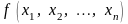 у
точці
називають вектор
у
точці
називають вектор
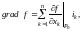
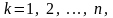 де
де
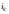 ‑
одиничні орти, а значення частинних
похідних
‑
одиничні орти, а значення частинних
похідних
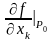 обчислені в точці
обчислені в точці
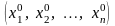 .
.
Властивості:
1.
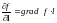 .
.
2.
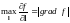 .
.
3. Якщо
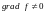 ,
то похідна
,
то похідна
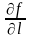 досягає найбільшого значення при
досягає найбільшого значення при
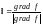 .
.