
- •Вступ до математичного аналізу Розділ 2
- •Послідовності.
- •Основні означення.
- •2.1.2. Обмежені та монотонні послідовності.
- •2.1.3. Збіжні та розбіжні послідовності.
- •2.1.4. Властивості збіжних послідовностей.
- •2.1.5. Число е.
- •2.1.7. Лема про вкладені відрізки.
- •2.1.8. Частинні послідовності.
- •2.1.9. Принцип збіжності Больцано-Коші.
- •2.1.10. Нескінченно малі та нескінченно великі послідовності.
- •2.1.11. Теореми про границі.
- •2.1.12. Границя відношення двох многочленів.
- •Границя функції.
- •2.2.1. Поняття границі функції.
- •2.2.2. Ліва та права границі функції.
- •Графічна ілюстрація
- •2.2.3. Теореми про границі функції.
- •2.2.4. Перша визначна границя.
- •2.2.5. Друга визначна границя.
- •2.2.6. Формула Ейлера.
- •2.3. Неперервність функції.
- •2.3.1. Основні поняття.
- •Графічна ілюстрація
- •2.3.2. Властивості неперервних функцій.
- •2.3.3. Розриви функції.
- •Можливі варіанти розриву функцій в точці
- •Наслідки з формул для визначних границь.
- •Порівняння нескінченно малих величин.
- •Шкала еквівалентних нескінченно малих величин.
- •Властивості функцій, неперервних на відрізку.
- •2.3.9. Рівномірна неперервність.
- •В прави для самостійного розв’язування
2.1.12. Границя відношення двох многочленів.
Правило:
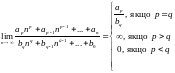
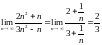 .
.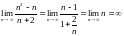 .
.
Границя функції.
2.2.1. Поняття границі функції.
Означення.
Нехай х0(а,
b)
і функція у
= f(x)
визначена на інтервалі (а,b)
за винятком, можливо, точки х0.
Якщо для будь-якої збіжної послідовності
хn
( ,
,
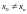 )
існує
)
існує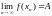 ,
то говорять, що функція
,
то говорять, що функція
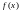 має границю А
при
має границю А
при
 .
.
Позначення:

Інше означення границі функції дав Коші:
Означення. (Коші) |
Границею
функції |
Позначення: 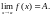
Графічна ілюстрація:
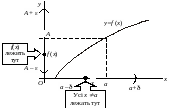
Рис. 2.2.
Пояснення. Для всіх х, що містяться поруч із точкою х=а, значення функції f(х) лежать біля А.
Д
овести
за означенням границі функції, що
 .
.
Застосовуємо означення границі, коли f(x)=5x–3, a=1, A=2.
Згідно з означенням потрібно показати, що для будь-якого >0 існує >0, таке що для всіх х
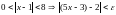 .
.
Маємо:

Отже,
можна взяти
 (рис.4.3).
(рис.4.3).
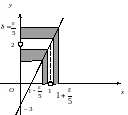
Рис. 2.3.
Для
функції
 нерівність
нерівність
 виконується, як тільки
виконується, як тільки
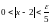 .
.
2.2.2. Ліва та права границі функції.
Означення. |
Правою
границею функції
маємо
Позначення:
|
|
|
Графічна ілюстрація
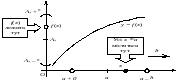
Рис. 2.4.
Означення. |
Лівою
границею функції
маємо
|
Позначення:  .
.
Інколи
границю
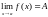 називають двосторонньою
границею, а границі
зліва та справа –односторонніми
границями.
називають двосторонньою
границею, а границі
зліва та справа –односторонніми
границями.
Зв’язок між односторонніми та двосторонніми границями. Функція має границю в точці х=а тоді і тільки тоді, коли існують границі зліва та справа в точці х=а і дорівнюють одна одній. Символічно:
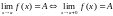 і
і
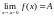 .
.
2.2.3. Теореми про границі функції.
Теорема
17. Якщо
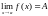 ,
то функція
,
то функція
 обмежена при
обмежена при
 .
.
Теорема
18. Якщо
 ,
то знайдеться такий -окіл
точки а,
де ця функція набуває значень, які мають
той самий знак, що й А.
,
то знайдеться такий -окіл
точки а,
де ця функція набуває значень, які мають
той самий знак, що й А.
Теорема
19. Якщо
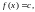 то
то
 .
.
Теорема
20. Якщо

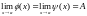 ,
то існує границя
.
,
то існує границя
.
Теорема
21. Якщо існують границі
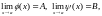 то виконуються такі співвідношення:
то виконуються такі співвідношення:
1)
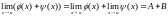 ;
;
2)
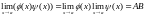 ;
;
3)
 ,
якщо
,
якщо
 .
.
2.2.4. Перша визначна границя.
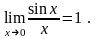
Доведення. З рис. 2.5 дістаємо:

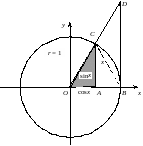
Рис. 2.5.
Доведемо,
що коли х0,
то сosx1,
причому з рисунка бачимо:
 .
.
За теоремою 7 про «охоплену» послідовність (п. 4.1.4):
 ,
,
тобто
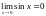 .
.
Тоді
 .
.
Отже,
 .
.
Графічна
ілюстрація .
.

Рис. 2.6.
Наслідки:
1.
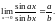

2.
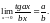
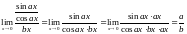
3.
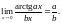
 .
.
2.2.5. Друга визначна границя.
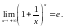
Доведення.
1. Припустимо, що
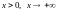 .
Для будь-якого х
знайдеться натуральне число n,
таке що
.
Для будь-якого х
знайдеться натуральне число n,
таке що
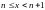 .
Тоді
.
Тоді
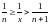 ,
,
або
 .
.
Якщо велике число піднесемо до великого степеня, нерівність лише підсилиться. Дістаємо:
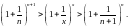
Обчислимо границі:
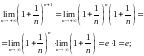

За теоремою 7 про «охоплену» послідовність маємо:
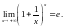
2. Нехай
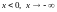 .
Знайдемо
.
Знайдемо
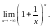
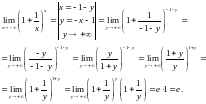
Наслідки:
1.


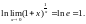
2.

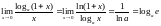 .
.
3.

 .
.
4.
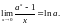
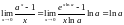 .
.
5.

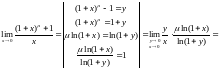
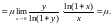
У частинному випадку
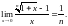

 при х,
що прямує до а,
називається число А,
якщо для будь-якого
існує число
при х,
що прямує до а,
називається число А,
якщо для будь-якого
існує число
 ,
таке що для всіх х,
які задовольняють нерівність випливає
,
таке що для всіх х,
які задовольняють нерівність випливає 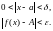
 ,
коли х
прямує до а
справа, називається число l,
таке що
існує
,
при якому для всіх х,
що задовольняють нерівність
,
коли х
прямує до а
справа, називається число l,
таке що
існує
,
при якому для всіх х,
що задовольняють нерівність
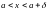 ,
,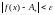 .
. .
.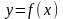 ,
коли х
прямує до а
зліва, називається число A–,
таке що при будь-якому
існує 0
таке, що для всіх х,які
задовольняють нерівність
,
коли х
прямує до а
зліва, називається число A–,
таке що при будь-якому
існує 0
таке, що для всіх х,які
задовольняють нерівність
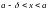 ,
,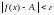 .
.