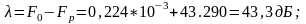- •Федеральное государственное автономное образовательное учреждение высшего профессионального образования «южный федеральный университет»
- •Кафедра систем автоматического управления
- •Пояснительная записка
- •«Фильтры нижних частот»
- •2.2. Конверторные фильтры нижних и верхних частот 12
- •Введение
- •Характеристики и параметры фильтров
- •Конструирование функций передачи фильтров
- •Синтез базовой матрицы низкочувствительных фильтров
- •2. Конверторные фильтры
- •2.1. Синтез лестничныхLc-фильтров
- •2.2. Конверторные фильтры нижних и верхних частот
- •2.3. Полосовые конверторные фильтры
- •3. Техническое задание
- •3.1. Исходные данные к проектированию
- •3.2. Структурная схема lc-прототипа 5-го порядка
- •3.3. Расчет схемы
- •3.4. Определение граничной частоты полосы режекции
- •3.5. Моделирование схемы фильтра в Micro-Cap
- •3.6. Исследование фильтра для случая идеальных оу
- •3.7. Влияние частотных свойств оу (level 3) на ачх фильтра
- •Определим основные характеристики фильтра (при 3-м уровне оу):
- •3.8. Исследование стабильности ачх фильтра методом Монте-Карло
- •3.9. Определение динамических перегрузок на выводах всех оу
- •3.10. Описание выбранных схемных элементов (операционных усилителей, резисторов, конденсаторов).
- •4. Заключение
- •5. Список используемой литературы
3.2. Структурная схема lc-прототипа 5-го порядка
По исходным данным табл. 1 составим схему LC-прототипа 5-го порядка (рис. 3,а) и его матрицу сопротивлений. Разделив все строки этой матрицы наоператор , получим матрицу
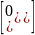 ,
(1)
,
(1)
описывающую схему рис. 5.1,б, где – конвертор сопротивления (см. рис. 2.4), который совместно с резистором реализует суперемкость .


а б
Рис.3. Лестничный LC- (а) и конверторный (б) ФНЧ-В 5-го порядка
Если теперь в матрице (1) произвести замену переменной , то с учетом обозначений рис. 3,б она примет вид
,
где
– суперемкость, реализуемая конвертором
и резистором
 .
.
3.3. Расчет схемы
а) Зададимся емкостью конденсатора и вычислим денормирующее сопротивление
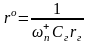 .
.
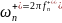 .
.
При
выборе значения
учитываем наличие такого значения в
ряду номинальных значений, а также
технологические и эксплуатационные
ограничения на минимальные и максимальные
значения параметров резисторов и
конденсаторов. Поскольку для фильтров
типа a и c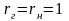 ,
емкость
равна емкости
.
,
емкость
равна емкости
.


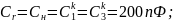

б) Рассчитаем сопротивления резисторов, имитирующих индуктивности схемы LC-фильтра:
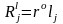 ,
,
где
 ;
при четном n и
при n нечетном.
;
при четном n и
при n нечетном.
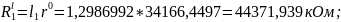


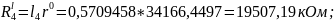
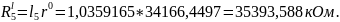
в)
Если для всех конверторов задать
одинаковые значения сопротивлений
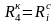 и одинаковые емкости
и одинаковые емкости
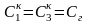 ,
то сопротивление резистора
,
то сопротивление резистора
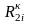 i-го
конвертора (
i-го
конвертора (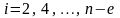 )
определится из соотношения
)
определится из соотношения
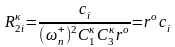
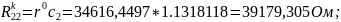
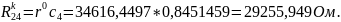
г)
Сопротивление резистора
,
шунтирующего конденсатор
,
выбираем из условия
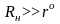 ,
а сопротивление резистора
,
включенного параллельно конденсатору
,
вычислим из соотношения
,
а сопротивление резистора
,
включенного параллельно конденсатору
,
вычислим из соотношения
 либо
либо
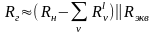 ,
,
что
непринципиально, если сопротивление
неинвертирующего входа ОУ
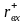 ,
а точнее
,
а точнее
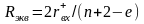 ,
гораздо больше
(
,
гораздо больше
(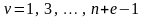 ).
Поскольку на этом этапе проектирования
тип ОУ не выбран, предварительно примем
).
Поскольку на этом этапе проектирования
тип ОУ не выбран, предварительно примем
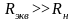 .
.

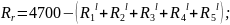
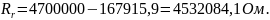
3.4. Определение граничной частоты полосы режекции
Поскольку параметры
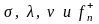 известны, а
известны, а
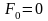 дБ
получили в результате расчета буферного
усилителя, определим граничную частоту
полосы режекции из выражения
дБ
получили в результате расчета буферного
усилителя, определим граничную частоту
полосы режекции из выражения
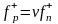 ;
;
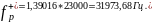
3.5. Моделирование схемы фильтра в Micro-Cap
По результатам расчета составим схему
фильтра в программе Micro-Cap
(рис. 4). Резисторам и конденсаторам
зададим допустимое отклонение параметров
от расчетных, составив описание новой
модели (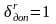 %,
%,
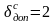 %).
%).

Рис.4. Принципиальная схема конверторного ФНЧ-В 5-го порядка
Поскольку в этой схеме наиболее полно используются высокочастотные свойства конвертора, выбираем операционный усилитель с небольшой площадью усиления – LF156.
3.6. Исследование фильтра для случая идеальных оу
В режиме Анализ/Частотные характеристики получим АЧХ общего вида и АЧХ в полосе пропускания для модели операционного фильтра 1 уровня, как показано на рисунке

Рис. 5.АЧХ общего вида и в полосе пропускания ФВЧ (L1)
На графике АЧХ общего
вида найдем и отметим (левым курсором)
точку наибольшего максимума в полосе
режекции (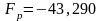 дБ
на рис. 5). На этом же графике для
подтверждения правильности выбора
точки отметим правым курсором точку
наименьшего максимума АЧХ в полосе
режекции (на рис. 5
– это –43,339 дБ). На графике АЧХ в полосе
пропускания найдем и отметим с помощью
курсоров точки, где коэффициент передачи
максимален (он же номинальный коэффициент
передачи
)
и минимален (на рис.5
дБ
на рис. 5). На этом же графике для
подтверждения правильности выбора
точки отметим правым курсором точку
наименьшего максимума АЧХ в полосе
режекции (на рис. 5
– это –43,339 дБ). На графике АЧХ в полосе
пропускания найдем и отметим с помощью
курсоров точки, где коэффициент передачи
максимален (он же номинальный коэффициент
передачи
)
и минимален (на рис.5 мдБ
и
мдБ
и
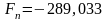 мдБ).
При этом разность между
и
мдБ).
При этом разность между
и
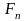 ,
т.е. неравномерность АЧХ в полосе
пропускания
,
т.е. неравномерность АЧХ в полосе
пропускания
 ,
в нашем случае составляет примерно
0,124 дБ, что близко к заданной неравномерности,
учитывая подъем АЧХ (
мдБ),
вызванный резисторами
и
.
,
в нашем случае составляет примерно
0,124 дБ, что близко к заданной неравномерности,
учитывая подъем АЧХ (
мдБ),
вызванный резисторами
и
.
Перейдем теперь к измерению граничных частот полос пропускания и режекции (рис.6)

Рис. 6. Определение граничных частот ФВЧ (L1)
По положению левого курсора на оси
частот определяется граничная частота
полосы пропускания
 кГц.
кГц.
Найдем неравномерность АЧХ в полосе пропускания ( ), гарантированное затухание в полосе режекции ( ) и коэффициент прямоугольности ( )