
- •Федеральное государственное автономное образовательное учреждение высшего профессионального образования «южный федеральный университет»
- •Кафедра систем автоматического управления
- •Пояснительная записка
- •«Фильтры нижних частот»
- •2.2. Конверторные фильтры нижних и верхних частот 12
- •Введение
- •Характеристики и параметры фильтров
- •Конструирование функций передачи фильтров
- •Синтез базовой матрицы низкочувствительных фильтров
- •2. Конверторные фильтры
- •2.1. Синтез лестничныхLc-фильтров
- •2.2. Конверторные фильтры нижних и верхних частот
- •2.3. Полосовые конверторные фильтры
- •3. Техническое задание
- •3.1. Исходные данные к проектированию
- •3.2. Структурная схема lc-прототипа 5-го порядка
- •3.3. Расчет схемы
- •3.4. Определение граничной частоты полосы режекции
- •3.5. Моделирование схемы фильтра в Micro-Cap
- •3.6. Исследование фильтра для случая идеальных оу
- •3.7. Влияние частотных свойств оу (level 3) на ачх фильтра
- •Определим основные характеристики фильтра (при 3-м уровне оу):
- •3.8. Исследование стабильности ачх фильтра методом Монте-Карло
- •3.9. Определение динамических перегрузок на выводах всех оу
- •3.10. Описание выбранных схемных элементов (операционных усилителей, резисторов, конденсаторов).
- •4. Заключение
- •5. Список используемой литературы
2.3. Полосовые конверторные фильтры
Чтобы
конверторная модель полосового
лестничного LC-фильтра
(см. рис. 2.3) не содержала избыточное
число реактивных элементов (конденсаторов),
все строки матрицы (2.8), за исключением
0-й строки у фильтров четкого порядка,
умножаются на оператор
,
в результате чего схемы полосовых
конверторных фильтров четного (6-го) и
нечетного (5-го) порядков примут вид,
показанный на рис. 2.10,а и б. В
этих схемах
 – i-й конвертор
сопротивления с двумя конденсаторами
– i-й конвертор
сопротивления с двумя конденсаторами
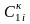 и
и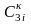 (
( );
);
 – резисторы, имитирующие соответствующие
катушки индуктивности схемы рис. 2.3;
– резисторы, имитирующие соответствующие
катушки индуктивности схемы рис. 2.3;
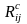 – резисторы, которые совместно с i-м
и j-м конверторами
имитируют соответствующие конденсаторы
схемы LC-фильтра
(заземленный конденсатор
– резисторы, которые совместно с i-м
и j-м конверторами
имитируют соответствующие конденсаторы
схемы LC-фильтра
(заземленный конденсатор
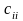 реализуется одним конвертором
совместно с резистором
реализуется одним конвертором
совместно с резистором
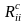 );
);
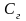 и
и
 – это преобразованные
– это преобразованные
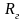 и
.
В схеме фильтра четного порядка (рис.
2.10,а) входная суперемкость
и
.
В схеме фильтра четного порядка (рис.
2.10,а) входная суперемкость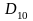 (емкость
(емкость
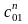 LC-фильтра)
реализуется конвертором
LC-фильтра)
реализуется конвертором
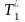 совместно с конденсатором
совместно с конденсатором
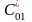 .
Конвертор
,
в отличие от
,
содержит один конденсатор
.
Конвертор
,
в отличие от
,
содержит один конденсатор
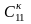 и три резистора
и три резистора
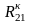 ,
,
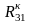 ,
,
 .
.
Составив матрицу проводимостей схемы конверторного фильтра (используя матрицу подсхемы рис. 2.7), путем сопоставления элементов этой матрицы и соответствующей матрицы LC-фильтра можно получить соотношения, связывающие параметры элементов этих схем:
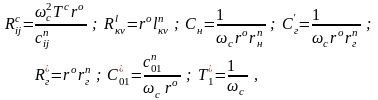 (2.14)
(2.14)
где
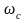 – центральная частота фильтра;
– денормирующее сопротивление;
– центральная частота фильтра;
– денормирующее сопротивление;
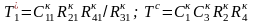 – параметр, одинаковый для всех
конверторов
;
параметр
– параметр, одинаковый для всех
конверторов
;
параметр
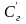 относится только к фильтру нечетного
порядка, а параметры, отмеченные «*» в
верхнем индексе, – только к фильтру
четного порядка;
относится только к фильтру нечетного
порядка, а параметры, отмеченные «*» в
верхнем индексе, – только к фильтру
четного порядка;
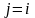 при
;
при
;
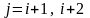 при
при
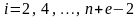 ;
;
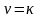 при
при
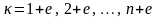 ;
;
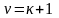 при
при
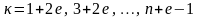 ;
;
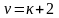 при
при
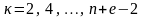 .
.
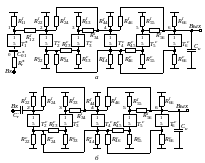
Рис. 2.10. Полосовые конверторные фильтры:
а – 6-гопорядка; б – 5-гопорядка
Если
полосовой LC-прототип
(см. рис. 2.3) оптимизирован по величине
коэффициентов динамической перегрузки
,
то и его конверторная модель (рис. 2.10)
не будет иметь динамических перегрузок
в κ-х(1,2, …) узлах. Однако на выходах
операционных усилителей, составляющих
конверторы сопротивления,
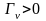 дБ
(
дБ
( ).
Оптимизация
).
Оптимизация
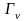 выполняется на этапе расчета схемы
конверторного фильтра путем соответствующего
выбора параметров элементов конверторов.
выполняется на этапе расчета схемы
конверторного фильтра путем соответствующего
выбора параметров элементов конверторов.
3. Техническое задание
По заданной таблице, в которой приведены значения элементов матриц симметричных фильтров синтезировать принципиальную схему фильтра нижних частот 5-го порядка, провести анализ полученной схемы, по результатам которого определить параметры фильтра.
3.1. Исходные данные к проектированию
Рассмотрим
конверторный фильтр типа С0515а-38, исходные
данные к проектированию которого
приведены в табл.1 (точнее, это данные
LC-ФНЧ-прототипа).
Граничная частота полосы пропускания
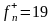 кГц.
кГц.
Таблица 1
С0525а–46 |
=0,2803 дБ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 =1,39016
=1,39016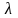 =43,34
дБ
=43,34
дБ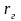 =
1
=
1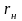 =
1
=
1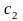 =1,1318118
=1,1318118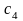 =0,8451459
=0,8451459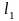 =1,2986992
=1,2986992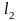 =0,1968325
=0,1968325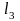 =1,8122495
=1,8122495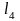 =0,5709458
=0,5709458 =1,0359165
=1,0359165