2.2. Конверторные фильтры нижних и верхних частот

Метод синтеза конверторных фильтров – это метод элементной имитации, когда каждый элемент LC-фильтра заменяется элементом или макроэлементом активной RC-техники, базовыми элементами которой являются операционные усилители, резисторы и конденсаторы.

Активным макроэлементом конверторных фильтров является конвертор комплексного сопротивления (конвертор сопротивления – КС), одна из наиболее удачных схем которого приведена на рис. 2.4. Он состоит из двух операционных усилителей (ОУ) и четырех пассивных элементов 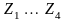(резисторов и конденсаторов). Конвертор по схеме рис. 2.4 по сравнению с составляющими его операционными усилителями имеет более широкий рабочий частотный диапазон, что объясняется взаимной компенсацией фазовых искажений усилителей ОУ1 и ОУ2. Для случая идеальных ОУ1 и ОУ2 схема рис. 2.4 описывается следующей матрицей проводимостей:

где – проводимости элементов КС; – коэффициенты усиления операционных усилителей.

Из выражений матричных элементов следует, что конвертор сопротивления – это невзаимная цепь, реализующая разные проводимости с разных входов (1 или 5), поэтому КС нельзя непосредственно использовать для имитации незаземленной индуктивности. В связи с этим при синтезе фильт­ра нижних частот схему BLC-ФНЧ-прототипа преобразуют таким образом, чтобы исключить незаземленные элементы, моделируемые с помощью конверторов сопротивления. Для этого проводимости всех элементов схемы B умножают на оператор s, в результате чего изменяется характер проводимостей элементов, и схема приобретает вид, показанный на рис. 2.5, где – конвертор сопротивления (рис. 2.4), который совместно с резистором 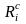реализует суперемкость . Выражение проводимости 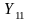в узле 1 конвертора T, нагруженного на элемент 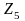, при имеет вид

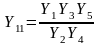
, (2.9)

где – проводимость κ-го элемента схемы рис. 2.4. Если в схеме конвертора и – конденсаторы (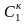 и ), а , 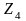и – резисторы ( , и ), то такой D-элемент будет суперемкостью, имеющей проводимость .

Поскольку в исходной схеме рис. 2.1,б параметры всех элементов нормированные, для определения реальных параметров элементов схемы рис. 2.5 необходимо вначале перейти от s к p ( ) и задаться денормирующим сопротивлением . Тогда

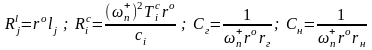, (2.10)

где ; – параметр КС.

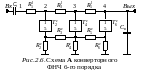В конверторной модели схемы Aлестничного LC-фильтра (рис. 2.6) заземленные суперемкости реализуются конверторами совместно с резисторами 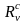, а незаземленные суперемкости – парой конверторов и совместно с резисторами ( ). Как и в случае схемы B, для определения реальных параметров элементов схемы рис. 2.6 необходимо в выражениях параметров элементов схемырис. 2.1,а перейти от s к p и задаться денормирующим сопротивлением . Поскольку в имитации незаземленных конденсаторов схемы рис. 2.1,а участвуют пары конверторов, необходимо задать для всех конверторов одинаковый параметр .

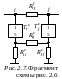Чтобы идентифицировать параметры элементов схем рис. 2.6 и 2.1,а, необходимо иметь матрицу проводимостей подсхемы, изображенной на рис. 2.7. Такая матрица составляется на основании матрицы проводимостей конвертора сопротивления (см. рис. 2.4) и при принимает вид

В соответствии с этой матрицей соотношения между параметрами элементов схем рис. 2.6 и рис. 2.1,а имеют следующий вид:

, (2.11)

где .

Так как у конверторного ФНЧ на входе и выходе вместо резисторов используются конденсаторы ( ), путь для постоянного тока неинвертирующего входа ОУ1 конверторов отсутствует, что приводит к большому постоянному напряжению дрейфа нуля ОУ, т.е. фильтр в таком виде неработоспособен. Чтобы уменьшить напряжение дрейфа ОУ, параллельно конденсаторам включаются резисторы :

,

где .

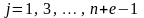Включение резисторов приводит к дополнительным искажениям АЧХ в полосе пропускания, поэтому сопротивление 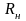необходимо выбирать как можно больше, но при этом учитывать, что с увеличением возрастает и паразитное постоянное напряжение на выходе фильтра, т.е. требуется разумный компромисс при выборе величины .

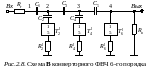В схемеВ лестничного ФВЧ (см. рис. 2.2,б) все катушки индуктивности заземлены, поэтому они могут быть непосредственно реализованы макроэлементами на основе конверторов сопротивления (см. рис. 2.4), если в качестве элементов , , и использовать резисторы, а в качестве элемента – конденсатор. В этом случае выражение проводимости в узле 1 схемы рис. 2.4 согласно (2.9) имеет вид

.

После замены катушек индуктивности их активными RC-моделями схема конверторного фильтра верхних частот примет вид, показанный на рис. 2.8. Проведя поэлементное сравнение схем рис. 2.8 и 2.2,б, можно получить расчетные соотношения для элементов конверторного ФВЧ на основе данных схемыВ LC-ФВЧ:

, (2.12)

где ; 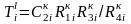– параметр i-го конвертора, а – денормирующее сопротивление, которым необходимо задаться.

В схемеАконверторного ФВЧ (рис. 2.9) конверторы используются для имитации как заземленных, так и незаземленных катушек индуктивности схемы рис. 2.2,а. Чтобы получить расчетные соотношения для схемы рис. 2.9,необходимо в выражениях проводимости элементов схемы рис. 2.2,а перейти от s к p и ввести денормирующее сопротивление . Поскольку в имитации каждой незаземленной индуктивности используется два конвертора сопротивления, параметры всех конверторов должны быть одинаковыми ( ). В этом случае параметры элементов схемы рис. 2.9 будут описываться следующими соотношениями:

, (2.13)

где .

Параметры элементов схем рис. 2.6, 2.8 и 2.9 могут быть выражены и через параметры элементов схемы рис. 2.1,б, если воспользоваться соотношениями (2.5) и (2.6).