3. Синтез базовой матрицы низкочувствительных фильтров

Метод синтеза базовой матрицы низкочувствительного фильтра

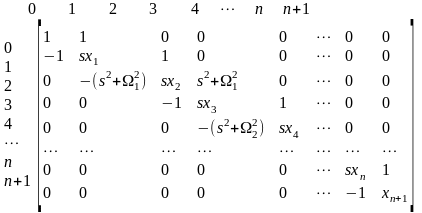(1.5)

основан на применении разложения функции входного иммитанса в непрерывную (цепную) дробь [1]. В (1.5) 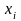– неизвестные переменные; – частота κ-го нуля функции передачи фильтра; n – порядок ФНЧ-прототипа.

Для матрицы (1.5) очевидны следующие соотношения между определителем 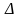и алгебраическими дополнениями:

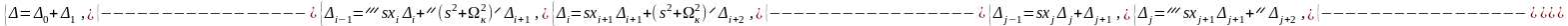
где 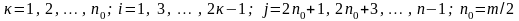– число нулей передачи; 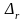– (r+1)–кратное алгебраическое дополнение, т.е. 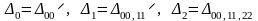и т. д.

Если вычеркнуть (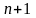 )-ю строку и ( )-й столбец в матрице (1.5), то отношение алгебраических дополнений можно рассматривать как входное сопротивление некоторой цепи без потерь. Алгебраические дополнения 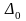и 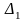можно выразить через знаменатель 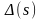функции передачи и числитель характеристической функции :

,

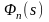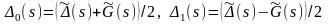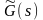где и – полиномы, нормированные к коэффициенту при старшем члене.

Синтез матрицы (1.5) выполняется путем последовательного выделения нулей передачи из функции входного сопротивления:

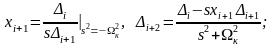
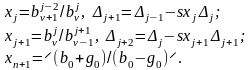
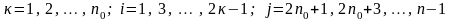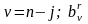
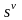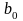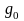
Здесь ;  коэффициент при полинома и  свободные члены полиномов 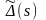и .

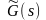2. Конверторные фильтры

2.1. Синтез лестничныхLc-фильтров

Конверторные фильтры представляют собой имитационные модели лестничныхLC-фильтров, которые отличаются наиболее низкой параметрической чувствительностью.

Матрица иммитансов лестничного LC-ФНЧ-прототипа может быть получена из матрицы (1.5) путем исключения всех четных строк и столбцов. В результате матрица (1.5) для фильтров четного (здесь ) и нечетного (здесь ) примет следующий вид:

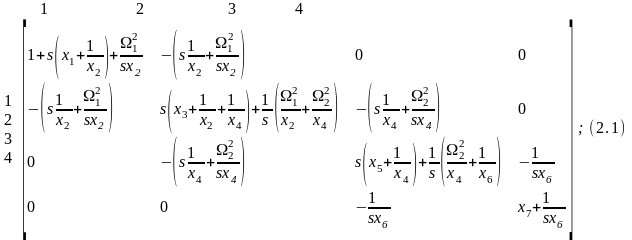
Учитывая, что элементы матрицы (1.5), как и матриц (2.1) и (2.2), величины безразмерные, матрицы (2.1) и (2.2) можно считать или матрицами сопротивлений, или матрицами проводимостей. Полагая, что матрицы (2.1) и (2.2) – это матрицы сопротивлений, им будет соответствовать схема LC-фильтра, изображенная на рис. 2.1,б (схема B). Схема нечетного ( ) порядка, описываемая матрицей сопротивлений (2.2), получается из схемы рис. 2.1,б, если положить 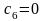. Соотношения между параметрами элементов схем B LC-фильтра и значениями коэффициентов 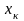матриц сопротивлений (2.1) и (2.2) имеют вид

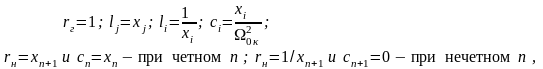(2.3)

где 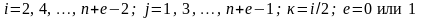в зависимости от четности или нечетности n.

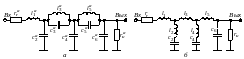
Рис. 2.1. СхемыА (а) и В (б) лестничного LC-ФНЧ-прототипа

Если считать матрицы (2.1) и (2.2) матрицами проводимостей, то, после изменения нумерации их строк и столбцов, они будут описывать схему Aлестничного LC-фильтра (рис. 2.1,а). В схеме фильтра нечетного порядка (нечетного n) 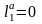. Соотношения между параметрами элементов схемыАи значениями коэффициентов матриц (2.1) и (2.2) имеют вид

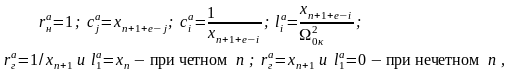(2.4)

где 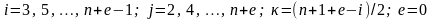при четном n и при n нечетном.

На основании соотношений (2.3) и (2.4) можно установить соответствия между параметрами элементов схемАи В:

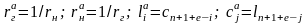, (2.5)

где .

Нули передачи в схеме рис. 2.1,а реализуются за счет включения параллельно катушкам индуктивности конденсаторов, а в схеме рис. 2.1,б – за счет включения катушек индуктивности последовательно с конденсаторами. У полиномиального лестничного LC-фильтра схемыА и В одинаковы, поскольку у них отсутствуют элементы, обеспечивающие реализацию нулей передачи (конденсаторы с нечетными номерами в схеме А и катушки индуктивности с четными номерами в схеме В).

При переходе от ФНЧ-прототипа к фильтру верхних частот используется стандартное частотное преобразование (1.4), применяемое к проводимостям элементов исходного фильтра:

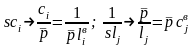
( ), что в результате приводит к формальной замене конденсаторов и катушек индуктивности в схеме рис. 2.1 на соответственно катушки индуктивности и конденсаторы (рис. 2.2) с параметрами

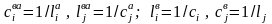; (2.6)

при этом значения сопротивлений резисторов не изменяются:

.

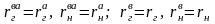Рис. 2.2. СхемыА (а) и В (б) лестничного LC-фильтра верхних частот

Переход от ФНЧ-прототипа к полосовому фильтру выполняется путем применения к проводимостям конденсаторов и сопротивлениям катушек индуктивности схемыА стандартного частотного преобразования (1.4):

;

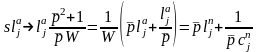
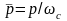( ), результатом чего становится формальная замена каждого конденсатора и каждой катушки индуктивности схемы рис. 2.1,а на соответственно параллельное и последовательное соединение конденсатора и катушки индуктивности, как показано на рис. 2.3.

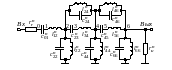
Рис. 2.3.Полосовой лестничный LC-фильтр 6-го порядка

Применительно к обозначениям, принятым на рис. 2.3, параметры элементов полосового фильтра связаны с параметрами элементов схемыА ФНЧ-прототипа следующими зависимостями:

,

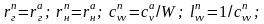
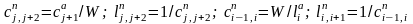где .

Учитывая соотношения (2.5) между параметрами элементов схемА и В, можно выразить параметры элементов полосового фильтра через параметры элементов схемы В ФНЧ-прототипа:

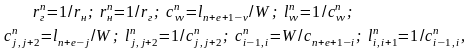(2.7)

где .

На рис. 2.3 изображена схема ПФ четного порядка, в отличие от которой в схеме нечетного порядка будут отсутствовать элементы .

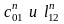Матрица проводимостей схемы рис. 2.3 имеет следующий вид:

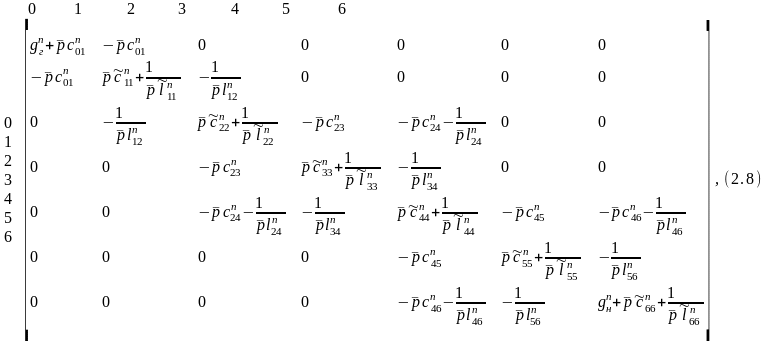
где 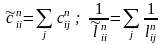, причем при j<i .

Если nнечетное, то отсутствуют 0-й и 1-й столбцы, а также 0-я и 1-я строки. При этом элемент на пересечении 2-го столбца и 2-й строки имеет вид .

Как у LC-фильтров, так и у их конверторных моделей наблюдаются динамические перегрузки, когда максимальное напряжение во внутренних узлах схемы превышает максимальное выходное напряжение, что характеризуется коэффициентами динамической перегрузки

,

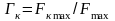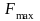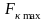где – максимальный коэффициент передачи с входа на выход фильтра; – максимальный коэффициент передачи с входа в κ-й узел схемы.

Чтобы уменьшить перегрузку в κ-м узле схемы, необходимо в этом узле увеличить проводимость собственных элементов (т.е. элементов, расположенных между этим узлом и общей шиной), а в тех узлах, где 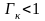, наоборот, уменьшить. Эти преобразования выполняются таким образом [1], чтобы не изменилась функция передачи фильтра, для чего каждый κ-й столбец и каждую κ-ю строку матрицы проводимостей фильтра умножают на коэффициент

,

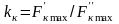где 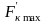– максимальные значения частных коэффициентов передачи до оптимизации ; – желаемое (или возможное) значение , которое получится после оптимизации .

Поскольку у лестничных ФНЧ и ФВЧ (см. рис. 2.1 и 2.2) собственные элементы узлов только одного типа, оптимизация коэффициентов динамической перегрузки у них невозможна, так как для этого потребовались бы элементы с отрицательными параметрами (емкостями, индуктивностями). У полосовых лестничных LC-фильтров оптимизация возможна, причем, если выбрать одинаковыми и равными максимальному коэффициенту передачи на выход фильтра, то полностью исключаются перегрузки в κ-х узлах (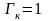 ), но при этом в некоторых случаях и здесь могут потребоваться элементы с отрицательными параметрами. Чтобы избежать применения таких элементов, необходимо изменить значение .

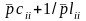После оптимизации коэффициентов динамической перегрузки вид матрицы (2.8) не изменится, но элементы матриц снечетнымиi теперь будут содержать и составляющие , что означает появление заземленных параллельных LC-контуров в соответствующих узлах схемы рис. 2.3.

Применение частотных преобразований (1.4) при синтезе LC-фильтров, как было показано выше, приводит к замене одних реактивных элементов другими, поэтому преобразования (1.4) называют еще реактансными преобразованиями.