
- •Федеральное государственное автономное образовательное учреждение высшего профессионального образования «южный федеральный университет»
- •Кафедра систем автоматического управления
- •Пояснительная записка
- •«Фильтры нижних частот»
- •2.2. Конверторные фильтры нижних и верхних частот 12
- •Введение
- •Характеристики и параметры фильтров
- •Конструирование функций передачи фильтров
- •Синтез базовой матрицы низкочувствительных фильтров
- •2. Конверторные фильтры
- •2.1. Синтез лестничныхLc-фильтров
- •2.2. Конверторные фильтры нижних и верхних частот
- •2.3. Полосовые конверторные фильтры
- •3. Техническое задание
- •3.1. Исходные данные к проектированию
- •3.2. Структурная схема lc-прототипа 5-го порядка
- •3.3. Расчет схемы
- •3.4. Определение граничной частоты полосы режекции
- •3.5. Моделирование схемы фильтра в Micro-Cap
- •3.6. Исследование фильтра для случая идеальных оу
- •3.7. Влияние частотных свойств оу (level 3) на ачх фильтра
- •Определим основные характеристики фильтра (при 3-м уровне оу):
- •3.8. Исследование стабильности ачх фильтра методом Монте-Карло
- •3.9. Определение динамических перегрузок на выводах всех оу
- •3.10. Описание выбранных схемных элементов (операционных усилителей, резисторов, конденсаторов).
- •4. Заключение
- •5. Список используемой литературы
МИНОБРНАУКИ РОССИИ
Федеральное государственное автономное образовательное учреждение высшего профессионального образования «южный федеральный университет»
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Кафедра систем автоматического управления

Пояснительная записка
к курсовой работе на тему:
«Фильтры нижних частот»
по курсу:
«Электроника»
Выполнил:
Студент группы А-21
Евтенко В.Н.
___________________
Проверил:
доцент каф. САУ
Христич В.В.
_____________________
«___» ____________ 2013г.
Таганрог 2013 г.
Содержани
Федеральное государственное автономное образовательное 1
учреждение высшего профессионального образования 1
«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» 1
1. ВВЕДЕНИЕ 5
1.1. Характеристики и параметры фильтров 5
1.2. Конструирование функций передачи фильтров 7
1.3. Синтез базовой матрицы низкочувствительных фильтров 9
2. КОНВЕРТОРНЫЕ ФИЛЬТРЫ 10
2.1. Синтез лестничныхLC-фильтров 10
2.2. Конверторные фильтры нижних и верхних частот 15
2.3. Полосовые конверторные фильтры 18
3. ТЕХНИЧЕСКОЕ ЗАДАНИЕ 20
3.1. Исходные данные к проектированию 20
3.2. Структурная схема LC-прототипа 5-го порядка 20
3.3. Расчет схемы 21
3.4. Определение граничной частоты полосы режекции 22
3.5. Моделирование схемы фильтра в Micro-Cap 22
3.6. Исследование фильтра для случая идеальных ОУ 23
3.7. Влияние частотных свойств ОУ (LEVEL 3) на АЧХ фильтра 24
3.8. Исследование стабильности АЧХ фильтра методом Монте-Карло 26
3.9. Определение динамических перегрузок на выводах всех ОУ 27
3.10. Описание выбранных схемных элементов (операционных усилителей, резисторов, конденсаторов). 28
4. ЗАКЛЮЧЕНИЕ 30
5. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ 31
1. ВВЕДЕНИЕ 3
1.1. Характеристики и параметры фильтров 3
1.2. Конструирование функций передачи фильтров 5
1.3. Синтез базовой матрицы низкочувствительных фильтров 7
2. КОНВЕРТОРНЫЕ ФИЛЬТРЫ 8
2.1. Синтез лестничныхLC-фильтров 8
2.2. Конверторные фильтры нижних и верхних частот 12
2.3. Полосовые конверторные фильтры 15
3. ТЕХНИЧЕСКОЕ ЗАДАНИЕ 17
3.1. Исходные данные к проектированию 17
3.2. Структурная схема LC-прототипа 5-го порядка 17
3.3. Расчет схемы 18
3.4. Определение граничной частоты полосы режекции 19
3.5. Моделирование схемы фильтра в Micro-Cap 20
3.6. Исследование фильтра для случая идеальных ОУ 20
3.7. Влияние частотных свойств ОУ (LEVEL 3) на АЧХ фильтра 22
3.8. Исследование стабильности АЧХ фильтра методом Монте-Карло 23
3.9. Определение динамических перегрузок на выводах всех ОУ 24
3.10. Описание выбранных схемных элементов (операционных усилителей, резисторов, конденсаторов). 25
4. ЗАКЛЮЧЕНИЕ 27
5. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ 28
Введение
Характеристики и параметры фильтров
В общем случае электрический фильтр – это цепь с заданной реакцией на данное воздействие. Под частотным фильтром понимается устройство, пропускающее сигналы одних частот и задерживающее сигналы других частот. Область частот, в которой сигналы пропускаются фильтром, называется полосой пропускания, а в которой задерживаются – полосой режекции. Между полосой пропускания и полосой режекции расположена переходная область.
 Взаимное
положение полос пропускания и режекции
является классификационным признаком
различных типов фильтров. По этому
признаку фильтры
подразделяются
на ФНЧ – фильтры нижних частот, ФВЧ –
фильтры верхних частот, ПФ – полосовые
фильтры и РФ – режекторныефильтры.
Общий вид их амплитудно-частотных
характеристик
(АЧХ) показан
на рис. 1.1. Они могут быть как колебательными
(в частности, равноволновыми), так и
монотонными (на рис. 1.1 изображены
равноволновые АЧХ), причем не обязательно
одинаковой формы в полосах пропускания
и режекции. Нижняя и верхняя
граничные частоты
полосы пропускания (
Взаимное
положение полос пропускания и режекции
является классификационным признаком
различных типов фильтров. По этому
признаку фильтры
подразделяются
на ФНЧ – фильтры нижних частот, ФВЧ –
фильтры верхних частот, ПФ – полосовые
фильтры и РФ – режекторныефильтры.
Общий вид их амплитудно-частотных
характеристик
(АЧХ) показан
на рис. 1.1. Они могут быть как колебательными
(в частности, равноволновыми), так и
монотонными (на рис. 1.1 изображены
равноволновые АЧХ), причем не обязательно
одинаковой формы в полосах пропускания
и режекции. Нижняя и верхняя
граничные частоты
полосы пропускания (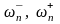 )
и полосы режекции (
)
и полосы режекции (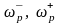 )
являются параметрами фильтра (у полосового
фильтра две полосы режекции, а у
режекторного – две полосы пропускания).
В пределах полосы пропускания модуль
функции передачи фильтра
)
являются параметрами фильтра (у полосового
фильтра две полосы режекции, а у
режекторного – две полосы пропускания).
В пределах полосы пропускания модуль
функции передачи фильтра
 должен быть постоянен с заданной
величиной ошибки
должен быть постоянен с заданной
величиной ошибки
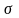 ,
а в пределах полосы режекции не должен
превышать некоторого малого значения
,
а в пределах полосы режекции не должен
превышать некоторого малого значения
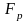 .
Параметр
.
Параметр
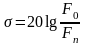
называется неравномерностью амплитудно-частотной характеристики в полосе пропускания, а

– гарантированным
затуханием в полосе режекции ( измеряются в децибелах). Чем уже
переходная область между полосой
пропускания и полосой режекции, тем
выше селективность (избирательность)
фильтра, т.е. тем меньше (ближе к единице)
коэффициент прямоугольности (
измеряются в децибелах). Чем уже
переходная область между полосой
пропускания и полосой режекции, тем
выше селективность (избирательность)
фильтра, т.е. тем меньше (ближе к единице)
коэффициент прямоугольности (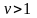 ),
который для разных типов фильтров имеет
следующие выражения:
),
который для разных типов фильтров имеет
следующие выражения:
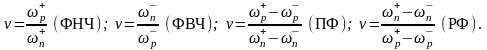
Стабильность (неизменность) амплитудно-частотной характеристики фильтра зависит как от стабильности параметров схемных элементов, так и степени их влияния на АЧХ, что оценивается коэффициентами параметрической чувствительности АЧХ в полосе пропускания и полосе режекции:
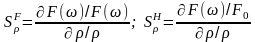 ,
,
где
 – относительная чувствительность АЧХ
в полосе пропускания;
– относительная чувствительность АЧХ
в полосе пропускания;
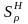 –
полуотносительная чувствительность
АЧХ в полосе режекции;
–
полуотносительная чувствительность
АЧХ в полосе режекции;
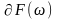 – приращение модуля функции передачи
при бесконечно малом относительном
приращении (
– приращение модуля функции передачи
при бесконечно малом относительном
приращении ( )
параметра
)
параметра
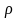 i-го
схемного элемента;
i-го
схемного элемента;
 – номинальный (максимальный) коэффициент
передачи фильтра в полосе пропускания.
– номинальный (максимальный) коэффициент
передачи фильтра в полосе пропускания.
Чтобы оценить дестабилизирующее действие всех элементов схемы, используется или матрица чувствительностей, или коэффициенты многопараметрической чувствительности в полосе пропускания и полосе режекции:
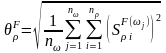 ;
;
 ,
,
где
 и
и
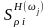 – чувствительности АЧХ на частоте
– чувствительности АЧХ на частоте
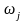 к i-му
схемному элементу соответственно в
полосе пропускания и полосе режекции
(
к i-му
схемному элементу соответственно в
полосе пропускания и полосе режекции
( );
);
 – число дестабилизирующих элементов;
– число дестабилизирующих элементов;
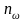 –
число точек частотного диапазона
анализа.
–
число точек частотного диапазона
анализа.
Эти меры чувствительности удобно использовать на этапе синтеза различных структур фильтров и их вариантов. На этапе проектирования промышленных образцов используются статистические меры оценки стабильности характеристик фильтров, в частности многопараметрическая статистическая чувствительность. Статистические характеристики спроектированного изделия определяются методом Монте-Карло.
По характеру влияния на стабильность активного RC-фильтра все его пассивные элементы можно разделить на две группы. К первой группе относятся элементы, в основном определяющие положение нулей и полюсов передаточной функции фильтра и характеризующие значения постоянных времени звеньев. Эти элементы оказывают доминирующее влияние на стабильность фильтра, причем тем большее, чем выше его селективность. Ко второй группе относятся элементы, определяющие коэффициенты передачи звеньев с различных входов. Поскольку коэффициенты передачи звеньев характеризуются отношением параметров однотипных элементов (резисторов) и чувствительность АЧХ к этим элементам не зависит от селективных свойств фильтра, степень их влияния на стабильность АЧХ вторична и при оптимизации чувствительности чаще всего не учитывается.
АктивныйRC-фильтр, как и другие линейные электронные устройства, может работать только в определенном диапазоне входных (выходных) напряжений, т.е. в определенном динамическом диапазоне
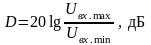 ,
,
нижний
уровень (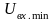 )
которого ограничен величиной шумов
электронных компонентов, а верхний
уровень (
)
которого ограничен величиной шумов
электронных компонентов, а верхний
уровень (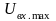 )
– допустимыми нелинейными искажениями
сигнала, возникающими в результате
перегрузки усилителей, являющихся
компонентами активного RC-фильтра.
)
– допустимыми нелинейными искажениями
сигнала, возникающими в результате
перегрузки усилителей, являющихся
компонентами активного RC-фильтра.
Динамический диапазон уменьшается, если ограничения сигнала (динамические перегрузки) наступают во внутренних узлах схемы раньше, чем на выходе фильтра. Поэтому при синтезе фильтра предусматривается оптимизация максимальных коэффициентов передачи с входа фильтра в критические узлы его схемы.
